树立应用意识 提高学生素养

摘 要：以行程问题为背景的一次函数与一元一次方程综合应用题是近年中考中常见的题型.教师要重视基础，引导学生探寻通性通法，提炼解题模型，挖掘蕴含的数学思想.在提升学生解题能力的同时，训练学生的思维，树立学生的应用意识，从而提高学生的素养.

关键词：解题能力;数学思想;应用意识;学生素养

作者简介：罗强华（1984-），男，四川营山人，本科，中学一级教师，研究方向：中学数学教学与解题.

1 试题呈现

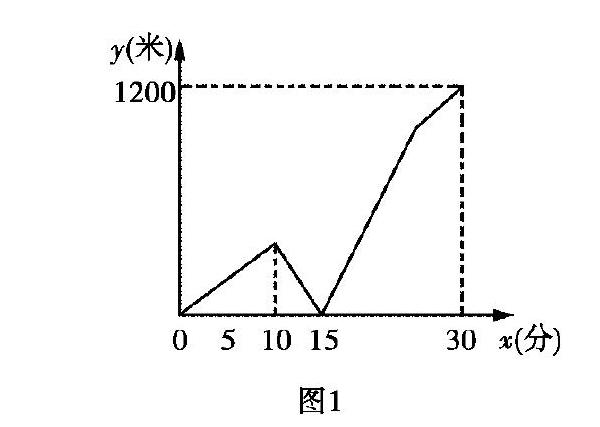
题目 （2018年重庆B卷第17题）一天早晨， 小玲从家出发匀速步行到学校.小玲出发一段时间后，她的妈妈发现小玲忘带了一件必需的学习用品，于是立即下楼骑自行车，沿小玲行进的路线，匀速去追小玲.妈妈追上小玲将学习用品交给小玲后，立即沿原路线匀速返回家里，但由于路上行人渐多，妈妈返回时骑车的速度只是原来速度的一半.小玲继续以原速度步行前往学校.妈妈与小玲之间的距离y（米）与小玲从家出发后步行的时间x（分）之间的关系如图1所示（小玲和妈妈上、下楼以及妈妈交学习用品给小玲耽搁的时间忽略不计）.当妈妈刚回到家时，小玲离学校的距离为米.

2 特色解读

2.1 贴近生活，体现应用功能

本题的背景是学生熟悉的生活情境，甚至是一些学生的亲身经历，让学生感到亲切而轻松，可以缓解考试中的紧张情绪，彰显了以学生为本的理念.题目贴近实际生活，让学生感受到数学来源于生活，又服务于生活，培养学生的应用意识和解决实际问题的能力，让学生明白学习数学的用处，体现了数学的应用功能.此外，题目的背景也展现了一个母亲对孩子的关爱和无私的付出，让学生在紧张的考试中还能体会到强大的母爱，体现了数学学科的育人功能，哪怕是中考也不忘对学生进行情感教育.

2.2 基于平常，給予正确导向

本题是一次函数与一元一次方程的综合应用题，涉及到一次函数图象的性质、行程问题中的追及问题和关系式“路程=速度×时间”等知识.重庆近几年的中考数学试卷中都出现了此类题目.题目虽有难度，但不是那种偏、难、繁、怪题，并非高不可攀.题目中涉及的基础知识、基本技能、基本思想和方法都是教师平常经常强调的重点，是学生所熟悉的内容.看到熟悉的题型，给考生带来希望，不至于望而却步，直接放弃.只要学生在平常认真练习、思考和体会，在考试时通过耐心细致地分析和解答，还是能够做出来的.但是又不能凭运气胡乱猜出答案.这对以后学生的学习和教师的工作都给予正确的导向，让学生明白在平时要踏实、勤奋和努力地学习，不能临阵磨枪，更不能投机取巧;也让教师清楚了今后教育教学工作中的重点，知道了如何更有效和有针对性地教育和引导学生.

2.3 数形结合，蕴含数学思想

数形结合是一种重要的数学思想.华罗庚曾说：“数缺形时少直观，形少数时难入微.数形结合百般好，隔离分家万事休.”在数学中，数和形是两个主要的研究对象，它们之间有着密切的联系.在一定条件下，数和形之间可以相互转化、互相关联.本题很好地应用和体现了数形结合思想，并将其与方程思想和函数思想相结合，展现出强大的逻辑思维和数学思想.

（1）题目中，妈妈与小玲之间的距离y（米）与小玲从家出发后步行的时间x（分）之间的关系通过函数图象表示出来.函数图象和题目条件中的数量相互结合，紧密联系在一起，互为补充.一些能力强的学生将函数图象和题目条件结合起来，就能领会题意，找到解决问题的方法，得出答案.

（2）对于一些理解力或想象力较弱的学生还可以根据题意画出线段图，利用几何直观来理解题意，解决问题.本题可以画出如图2所示的线段图.通过数形结合审题可知，家到学校的距离为1200米，小玲30分钟走完，

可以求出小玲的速度为40米/分.小玲离家10分钟时，妈妈去追她，5分钟后，妈妈追上小玲，可以求出妈妈追及的速度为120米/分和返回时的速度为60米/分.由此可求出妈妈返回的时间为10分钟，此时，小玲已经走了25分钟，还剩下5分钟的路程，从而求出小玲离学校的距离为200米.

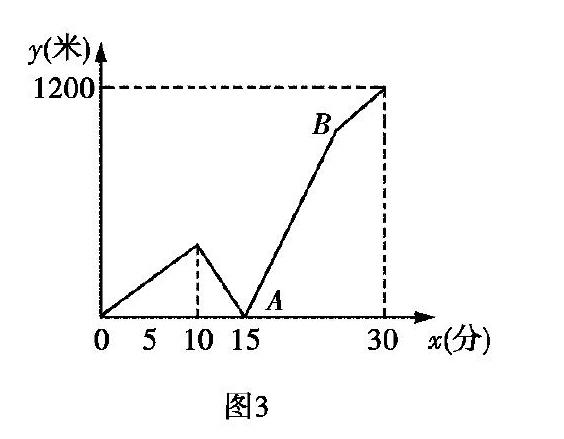
（3）在解题时，除了用一元一次方程的方法求解之外，还可以借助函数图象求出函数关系式，用解析法求解.根据题意可以求出图3中直线AB的函数解析式为：

y=100x-1500.当妈妈到家时，x=25，可求出y的值为1000，即小玲离家的距离为1000米，离学校的距离为200米.

2.4 运用模型，突出通性通法

纵观重庆近几年的中考数学试卷，此类题目不外乎是一次函数与相遇问题或追及问题的综合应用.考查的是平常所学习的核心知识和基本模型，突出了通性通法.

例如，本题涉及了追及问题，其线段图如图4所示，关系式为：“追者的行程-被追者的行程=间隔的距离”或“（追者速度-被追者速度）×追及时间=间隔的距离”.

有时也涉及到相遇问题，其线段图如图5所示，关系式为：

“甲的行程+乙的行程=总路程”或“（甲的速度+乙的速度）×相遇时间=总路程”.

解决此类问题的基本思路是：首先结合函数图象和线段图审懂题意，特别是函数图象中的自变量、因变量和每个交点所表示的实际意义，这是解决问题的前提;然后根据题意并运用模型求出相关人员的速度，这是解决问题的关键;最后求出答案.

3 教学导向分析

3.1 重视基础，提升解题能力

《义务教育数学课程标准（2011年版）》明确提出：通过义务教育阶段的数学学习，学生能获得适应生活和进一步发展所必须的数学基础知识、基本技能、基本思想和基本活动经验[1].即我们现在常说的“四基”.这是学生应用数学解决问题的重要而强大的支撑.教师在平常教学中，要重视基础知识教学，要求学生理解并掌握概念、公式和性质等;加强训练学生的基本技能，特别是分析能力、理解能力、推理能力、运算能力和应用能力等;不断向学生渗透数学思想和方法.