超级栅板衍射强度角谱的数学探究

王春艳，邬志强，王厚增

（齐齐哈尔大学 理学院，黑龙江 齐齐哈尔 161006）

1 引言及预备知识

声学超表面是声学超材料的分支，以其灵活的声波调控特性成为超材料领域的研究热点[1]．声超表面是由周期性亚波长元素组成的，通过合理设计周期元素的位置，超表面可以实现声波的多种功能[2]．为了控制波迹，超表面必须在不同的位置提供相应的相位剖面．这种相位分布通常是由广义衍射定律推导出来的，从而导致了对工作频率的固有依赖[3]．因此，奇异相位使得超表面只能在窄带内工作．作为一种新兴的超表面，人工超级光栅由于具有比普通相位光栅更多的组合功能和更优越的性能而备受关注[4]．超级栅板衍射强度特性的研究是至关重要的，在理论上主要用角谱方程来研究衍射特性，本文利用数学的方法研究其衍射角谱方程．

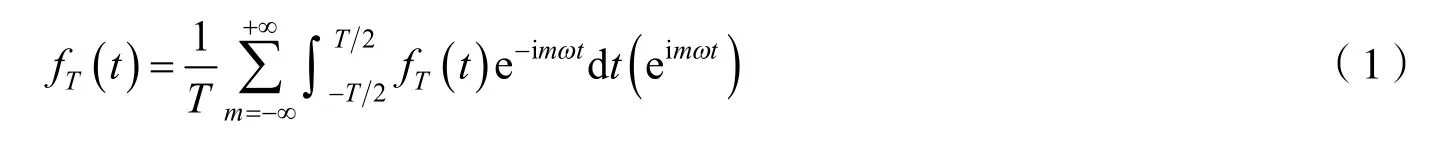
2 主要结果及证明

定理衍射强度的角谱为

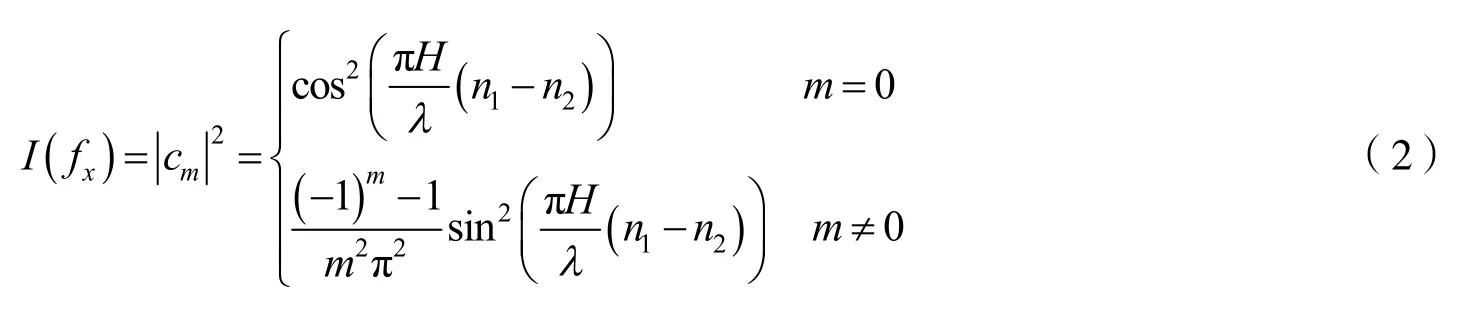
证明根据规则相位光栅的原理，当平面波垂直入射到栅板时，栅板的衍射角度满足光栅方程，其中：m（m=0,±1,±2,…）为衍射阶数；θm为第m个衍射阶数的衍射角；λ为入射波长；d为栅板常数，这里栅板常数d固定为孔径尺寸a的2倍，也就是d=2a．根据声学理论[5]，当单位振幅的平面波垂直入射于相位光栅时，全栅板角谱等于光栅透射率函数t的Fourier变换，衍射强度谱是Fourier变换F（t）的平方，栅板的透射率t（x）可以结合栅栏和孔径的透射率得到．当平面波透过相位栅板时，栅板和孔径的相位延迟分别为，其中：n,n分别为栅板和孔径的衍射指数；H为栅12栏高度．因此，栅板透射率函数t（x）可以表示为

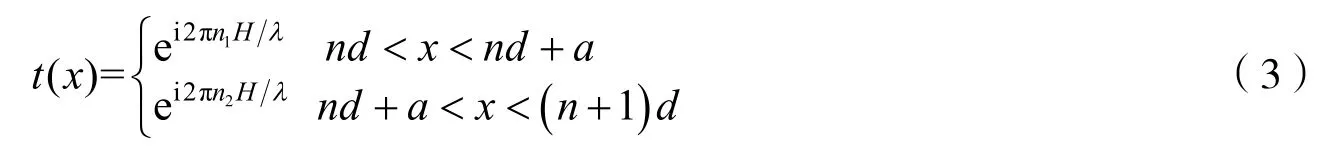
其中：n=0,±1, 2,…．

根据t(x)的Fourier展开，得到，其中：则第n阶衍射强度的角谱为

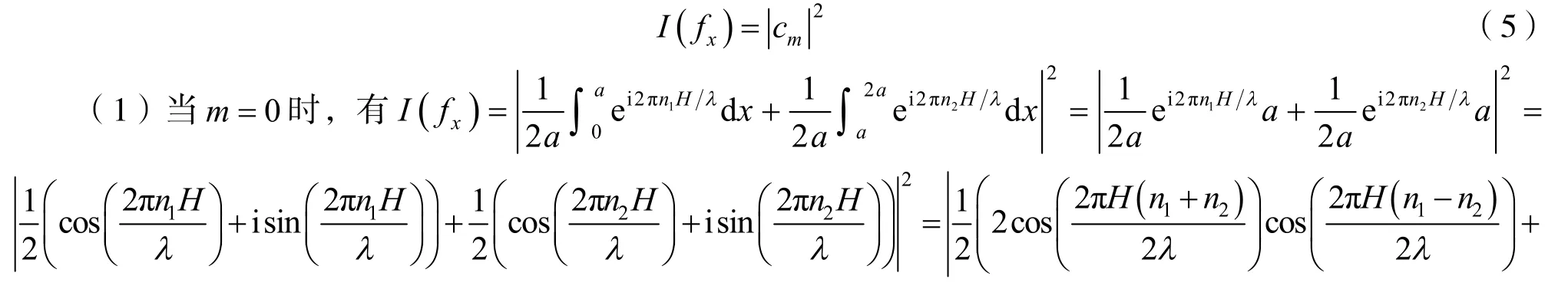
通过声波的衍射强度的角谱方程，可以进一步研究声波衍射的分布情况，从而设计人工超表面的分布结构．