数据分布特性对空调系统能耗预测的影响

于 丹， 王丽娜， 曹 勇， 崔治国， 王 晨， 唐艳南

(1.北京建筑大学环境与能源工程学院，北京 100044；2.中国建筑科学研究院有限公司，北京 100013)

建筑及其相关行业的发展严重影响全球的经济、能源、民生与环境等各个方面。根据国际能源署的统计，建筑业约消耗了全球能源的32%[1]。根据最新的统计，中国建筑能源消费总量为8.57亿t标准煤，约占全国能源消费总量的20%，其中公共建筑能耗2.92亿t标准煤，占建筑能耗总量的34%[2]。从建筑的全生命周期角度进行能耗分析，发现运行与维护阶段的能耗可以占到建筑总生命周期能源消耗的80%～90%[1]。目前中国公共建筑中，暖通空调系统是最主要的耗能设备，其运行能耗可以占到建筑能耗的50%～60%[3]。因此，建筑行业以及空调系统的节能具有十分重要的意义。

建筑能耗分析是建筑能源需求侧管理的重要实现步骤之一。准确的建筑能耗预测为建筑能源供应与调度、多能源耦合供能系统提供了依据；精确的能耗预测是空调系统节能控制的关键步骤之一，是实现预测控制、优化控制的基础[4-5]。

当前的研究中，对空调系统的能耗预测主要是在实际运行数据的基础上，采用机器学习算法的方法。目前中外关于建筑能耗预测的算法种类繁多，其中比较典型的有广义线性回归分析算法、神经网络算法、支持向量机算法等。如文献[6-7]通过分析建筑能耗的主要影响因素、不同因子的敏感性，利用多元线性回归方法分别建立了办公建筑、商场建筑的空调能耗预测模型。研究结果表明，多元线性回归模型具有良好的数据拟合能力。该类方法在进行负荷预测时，需要进行影响性分析或敏感性分析，以找出对模型影响较大的因素。文献[8-10]利用人工神经网络对非线性问题具有良好逼近能力的特性，建立了建筑能耗的人工神经网络模型。人工神经网络模型具有预测精度高、模型训练时间长的特点。文献[11-13]利用支持向量类算法进行建筑能耗的预测建模，相对于人工神经网络算法，支持向量类算法具有训练时间短的优点，由于其对缺失数据敏感，在工程应用方面有其不足。

然而，众多的机器学习算法大多都假设数据之间相互独立，即数据分布服从正态分布[14]。事实上，由于数据之间本身具有相关性，数据的分布往往并不服从正态分布，如果未对数据进行任何处理，直接作为能耗预测的输入条件，则能耗预测的结果会存在一定的误差。相关方面在当前的研究中鲜有提及。

从数据的分布特性出发，对不服从正态分布特性的原始数据进行适当的数据变换处理，作为提升能耗预测效果的重要技术手段。对实际的空调系统能耗进行预测，发现数据的分布特性对能耗预测影响巨大，合适的数据变换能大幅提升机器学习算法能耗预测的效果(准确度)。

1 数据的分布特性及其描述

在数学理论中，常常倾向于将某一可能发生的事件称为随机事件，将事件可能出现的各种情况量值化，称之为该事件对应的随机变量，同时以数据分布的概率密度图直观表达数据的分布特性[15]。

正态分布是一种重要的数据分布，对于随机变量x，若其数据分布为正态分布(称x服从参数为(μ,σ)的正态分布)，则其概率密度如式(1)所示，概率密度图如图1所示，从图形上看，其围绕x=μ成中心对称[15]。

(1)

式(1)中：f(x)为概率密度；μ为正态分布的均值；σ为正态分布的标准差。

图1 正态分布概率密度图Fig.1 Probability density diagram of normal distribution

在自然界中，若某一随机变量为独立随机变量(即受外界其他因素影响较小)，则其数据分布近似于正态分布。

然而，由于自然界各种因素之间相互影响，因而在实际中，某一单一随机变量的取值往往会偏离正态分布。

在数学上，常常用两个数学统计量来衡量数据分布偏离正态分布的程度。

1.1 偏度(skewness)

定义随机变量数据分布的标准三阶中心矩为偏度，即

(2)

式(2)中：skew(x)为偏度；μ为数据分布的均值；σ为数据分布的标准差。

偏度是描述数据分布偏斜方向和程度的统计量，是统计数据分布非对称程度的数字特征。对于正态分布而言，偏度为0。若偏度为小于0，则数据均值左侧的离散度比右侧强，其概率密度图如图2(a)所示；若偏度大于0，则数据均值左侧的离散度比右侧弱，其概率密度图如图2(b)所示。

图2 偏度分布概率密度图Fig.2 Probability density diagram of skewness distribution

1.2 峰度(kurtosis)

定义随机变量数据分布的标准四阶中心矩为峰度，即

(3)

式(3)中：kurt(x)为峰度；μ为数据分布的均值；σ为数据分布的标准差。

峰度是描述数据样本分布形态陡缓程度的统计量。该统计量与正态分布相比较，峰度为0表示该总体数据分布与正态分布的陡缓程度相同；峰度大于0表示该总体数据分布与正态分布相比较为陡峭；峰度小于0表示该总体数据分布与正态分布相比较为平坦。峰度的绝对值数值越大表示其分布形态的陡缓程度与正态分布的差异程度越大。不同峰度的数据分布概率密度图如图3所示。

图3 不同峰度分布概率密度图Fig.3 Probability density diagram of different kurtosis distribution

数据分布的偏度和峰度衡量了数据分布与正态分布的差异性，可以为为充分描述实际数据的分布特性规律提供量化的指标。

2 实际空调系统能耗数据特性与数据变换

为了衡量数据的分布特性对空调系统能耗预测的影响特性，选取了实际项目的运行数据，进行空调系统能耗预测。

2.1 数据来源与概况

项目位于吉林省长春市，建筑类型为超低能耗办公建筑。建筑面积约5 000 m2，其中绝大部分区域作为展厅用途，办公区域面积约950 m2。办公区域空调冷源采用变频多联式空调机组，设计冷负荷指标为25 W/m2。

该项目建立了完善的建筑能耗分项计量系统，实现了空调、照明、动力等各类用电的监测与计量。数据采集与传输频率为15 min一次。同时，建筑能耗分项计量系统监测了室外环境参数，主要有室外温度、室外相对湿度、太阳辐射度等。

选取空调系统连续的约4 000行数据，如表1所示。

表1 某实际项目的空调系统运行数据

实际的空调系统运行中由于各种原因，如停电、通信故障、传感器故障等原因，存在着数据缺失、数据异常等问题，在进行能耗预测工作之前，先进行数据预处理。本文的数据预处理采用课题组在数据预处理方面的既有工作成果和相关方法[16]。

2.2 原始数据分布特性

通过数据预处理得到相对干净的数据集合。对空调系统运行能耗数据作出概率密度分布图，如图4所示。

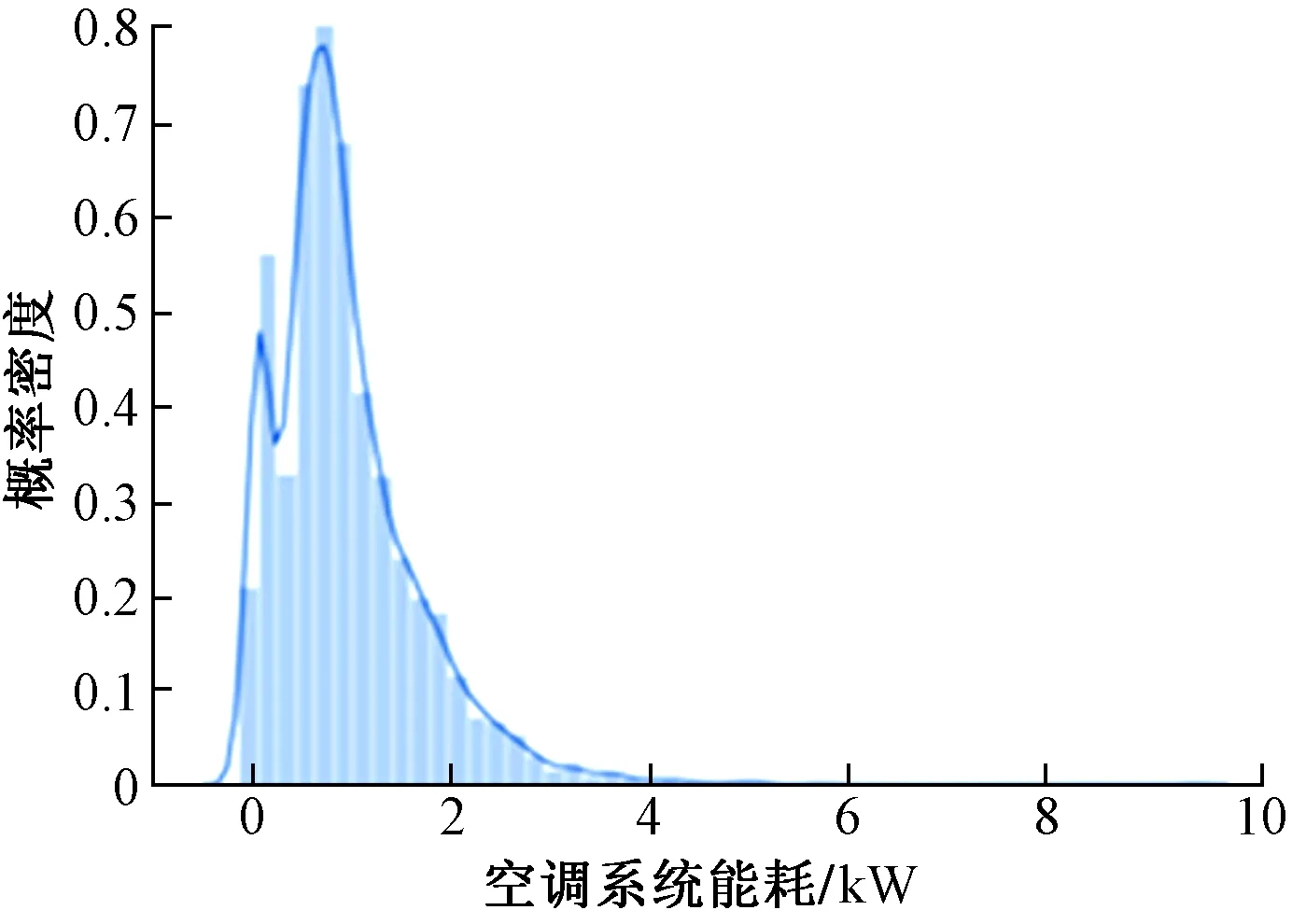
图4 空调系统能耗数据分布图Fig.4 Distribution chart of energy consumption data of air conditioning system

计算原始空调系统能耗数据的偏度和峰度，结果如表2所示。

表2 原始空调系统能耗数据的分布

从图4的分布图和表2的结果可以看出，原始数据的偏度和峰度都远远大于零，即数据远远偏离正态分布。

2.3 数据分布变换

原始数据远远偏离正态分布，为了能使得数据应用于机器学习算法能耗预测算法，需要对原始数据进行合适的数据变换。

根据数学理论和经验，选择对数变换，对原始数据进行数据变换。数据变换式为

datanew=log(dataraw+1)

(4)

式(4)中：dataraw为原始数据；datanew为对数变换后的数据。

用对数变换对空调系统能耗数据进行变换，变换后的数据分布如图5所示，计算数据的偏度和峰度如表3所示。

从图5的分布图和表 3 的结果可以看出，原始数据的偏度和峰度都大大降低，相对于原始数据，对数变换后的空调系统能耗数据分布更接近于正态分布。

图5 空调系统能耗数据分布图Fig.5 Distribution chart of energy consumption data of air conditioning system

统计量偏度峰度数值0.440.29

3 基于机器学习算法的空调系统能耗预测

3.1 能耗预测机器学习算法建模

3.1.1 原理

在机器学习中，常常把模型和数据表示为以下一组未知对应关系：

Model:features→labels

(5)

式(5)中：Model为机器学习算法；features和labels组成了一一对应的数据集合；features称为特征，即输入变量，labels称为标签，即输出变量。

在本文的空调系统能耗预测中，特征即为室外温度、室外相对湿度、太阳辐射度，标签为空调系统能耗。

在实际的机器学习过程中，通常将数据集随机分为2个部分，即训练集和验证集。通过在数据集上训练出能耗预测模型，然后将训练后的模型用于验证集，根据模型在验证集上的效果判别模型的优劣。在实际的能耗预测中，将数据随机分为2部分，训练集和验证集的比例约为4∶1。

3.1.2 预测模型

目前关于建筑能耗预测的典型算法有广义线性回归分析算法、神经网络算法、支持向量机算法等。

为了验证数据变换对能耗预测的影响程度，选择4种典型算法进行能耗预测工作。4种典型算法分别为广义线性回归算法中的岭回归(ridge regression)算法、支持向量回归(support vector regression, SVR)算法、人工神经网络(artificial neural network，ANN)算法、随机森林(random forest)算法[11]。相关算法的关键参数如表4所示(多次模型训练寻优的结果)。

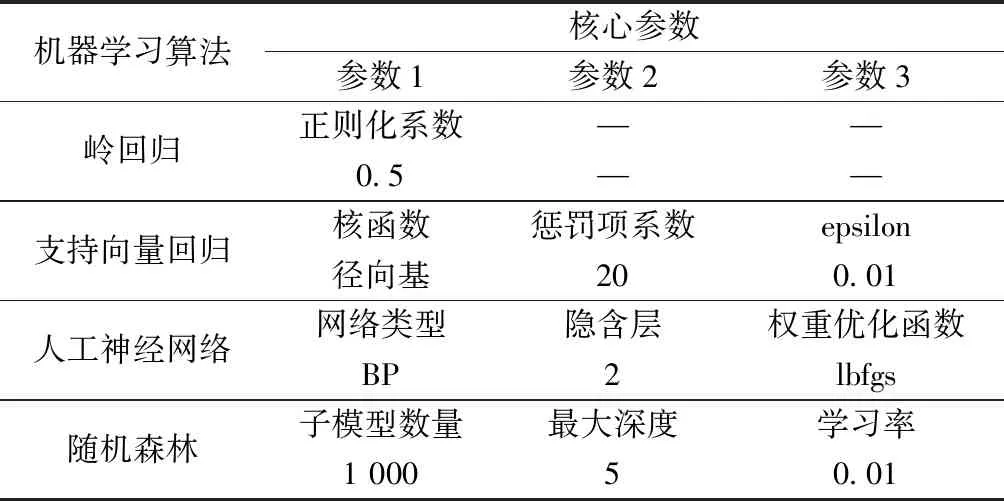
表4 能耗预测算法核心参数配置

3.1.3 误差分析

为了衡量机器学习算法能耗预测模型的效果，引入常见的2个模型评价指标作为判别模型优劣的依据，分别为均方根误差(root mean square error, RMSE)和R2统计量，分别如式(6)和式(7)所示。均方根误差RMSE越小，R2统计量越接近于1，说明模型预测效果越好。

(6)

式(6)中：m为数据样本的数量；ypred为算法预测值；ytrue为真实值。

(7)

式(7)中：SSres为模型预测值与真实值的残差平方和；SStot为模型预测值与真实值的离差平方和。

3.2 能耗预测结果与分析

根据以上的模型和误差分析，进行了以下两方面的能耗预测工作。

(1)对原始数据直接应用机器学习算法进行能耗预测。

(2)对经过数据变换后的空调系统数据应用机器学习算法进行能耗预测。

两次的能耗预测结果的均方根误差和R2统计量如表5和表6所示。

表5 机器学习算法能耗预测模型均方根误差结果

表6 机器学习算法能耗预测模型R2统计量结果

绘制出两次能耗预测的均方根误差和R2统计量变化图，如图6和图7所示。

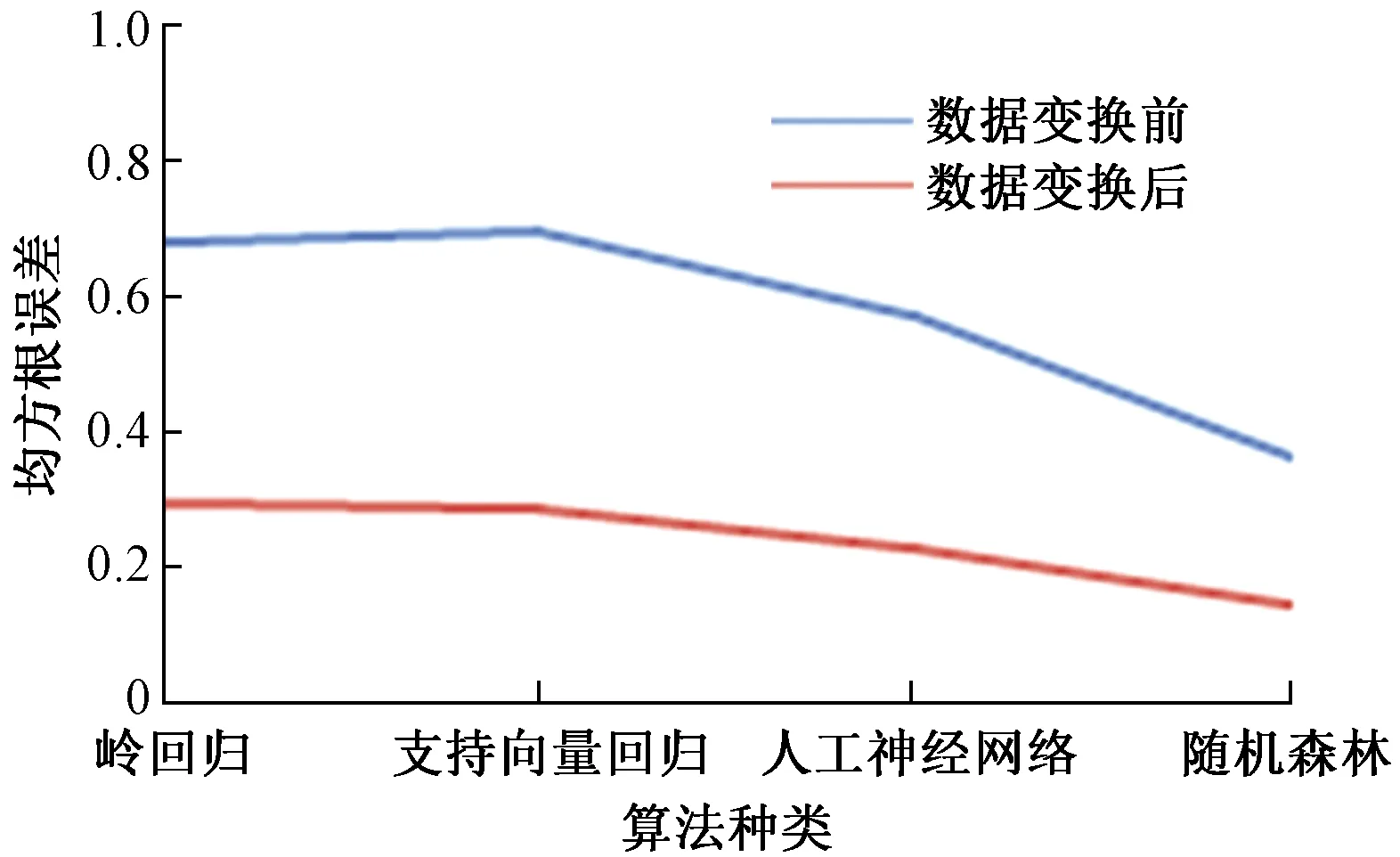
图6 两次能耗预测模型的均方根误差Fig.6 RMSE of the twice energy consumption prediction model

图7 两次能耗预测模型的R2统计量Fig.7 R2 of the twice energy consumption prediction model

分析表5和表6、图6和图7，可以看出，经过数据变换后，4种常见的机器学习算法在进行空调系统能耗预测时，均方根误差都得到了不同程度的降低，R2统计量都得到不同程度的提高。

通过多次的数据训练与能耗预测，得到相同的结论。因此，对原始的非正态分布数据进行合适的数据变换可以有效提高空调系统能耗预测模型的效果。

4 结论

现实生活中的数据分布并不呈现正态分布的特性，但是数据的正态分布特性(或接近于正态分布特性)是众多机器学习算法的重要前提假设之一。

基于空调系统的实际运行数据，分析了其运行能耗数据分布的非正态性，并给出了相应的数据变换，变换后的数据相对于原始数据更接近于正态分布。

采用常见的4种能耗预测机器学习算法，即广义线性回归算法、支持向量回归算法、人工神经网络算法、随机森林算法，分别基于原始运行数据和经过数据变换后的空调系统数据进行空调系统能耗预测。预测结果对比发现，经过数据变换，4种机器学习算法的预测效果都得到了不同程度的提高。即数据的分布特性对空调系统的能耗预测有着重要的影响，在进行能耗预测之前进行合适的数据变换可以有效提高能耗预测的效果。

另一方面，采用的都是常见的能耗预测算法，最好的随机森林算法预测模型的均方根误差和R2统计量分别为0.15和0.78，模型的预测效果有待于进一步提高。同时，空调系统能耗预测除了与本文中提到的室外温度、室外相对湿度、太阳辐射度相关，还与一些其他因素紧密相连，如室内温度、人员用能习惯等。如何优化模型、如何选择合适的建模参数，进一步提高能耗预测效果是本课题组的另一项重要工作。