一种强噪声微地震信号P震相初至拾取的新方法

王亚娟，李怀良，2，庹先国，2，3，沈 统

（1.西南科技大学核废物与环境安全国防重点学科实验室，四川绵阳621010；2.成都理工大学地质灾害防治与地质环境保护国家重点实验室，四川成都610059；3.四川轻化工大学，四川自贡643002）

我国页岩气资源丰富，其开发促进了能源结构的调整和改变[1]。其中，水力压裂为页岩气的勘探开发提供了重要的技术手段[2]，而水力压裂微地震监测则为页岩气优化开发方案的制定提供了重要的技术支持。通过微地震监测技术对微地震事件定位、能量大小估计及震源机理分析等可了解裂缝的形态分布及发育过程、裂缝间的相互作用、估算储层改造体积、进行储层应力分析和开展地震灾害评价[3-5]。

其中，精确的P 震相初至拾取是上述工作实施的重要基础步骤。虽然此项工作可以手工进行，但随着数据量的急剧增加，视觉分析已然成为一项非常耗时和繁琐的工作[6]。因此，有必要提供一种更高效、快速、客观、自动的P震相初至拾取方法。

现有的P震相初至拾取方法大部分来源于对天然地震数据的处理，例如：能量分析[7-10]、极化分析[11-13]、人工神经网络[14-15]、自回归技术[16-17]、高阶统计量[18-22]、小波变换[6]等，这些方法各有特点，在天然地震领域取得了较好的应用效果。其中，高阶统计量是识别非高斯信号的有效工具，SARAGIOTIS等[19]应用基于高阶统计函数的偏度和峰度函数来识别P震相到达时间。相对于偏度函数，峰度法对非高斯信号更加敏感，且对高斯噪声有一定的抑制作用。当信号受到相对较低的噪声污染时，该方法大多能较好地确定P震相的到达时。然而，在微地震监测领域，由于检波器自身的技术局限性以及外部监测环境等因素的影响，实际采集的微地震数据不可避免地与高频噪声和工频噪声混合在一起，信噪比较低且初动不明显。在这种情况下，峰度法大多效果不佳。

为提高峰度法对微地震信号的拾取精度，本文提出了一种基于特征函数构建的峰度与小波多尺度分解的P震相初至拾取新方法。考虑到各种噪声的随机性，该方法利用小波多尺度分解提取含强噪声微地震信号的主成分，将其高频信号剥离，提高微地震信号的质量。在获得有效信号后，构建其特征函数，并计算该特征函数序列的峰度值，该峰度值的全局最大斜率即为所拾取的初至点。

1 峰度法

峰度是衡量信号高斯度的四阶统计量。服从近似高斯分布的信号，其峰度值接近于0；而非高斯信号（如微地震事件）产生的峰度值较高。因此，峰度可以作为识别非高斯特征信号的有效统计工具[19]。其计算过程如下。

x（n）为微地震信号，其中，n＝1，2，…，为采样点个数。采用长度为M的移动时间窗口扫描微地震序列，当窗口从M滑动到n（M＜n）时，定义每个滑动窗口的峰度值计算公式为：

其中，

为计算微地震记录的峰度值序列，需设置一个移动时间窗口沿时间轴扫描微地震记录，窗口大小M＝200，移动步长为1，即1～200、2～201、3～202…。如图1所示，模拟一组信噪比为10 dB 的微地震信号，其信号主频为120 Hz，采样间隔为0.1667×10－3s，采样长度为2000 个采样点，设置P 震相初至为1000。在图1a中，A，B，C分别代表时间窗口移动的不同位置。时窗在沿时间轴移动的过程中，计算每个窗口位置的峰度值，由此得到描述微地震信号非高斯性的峰度曲线，为了与信号的横轴对齐，峰度曲线的横轴起点应为200，终点为2000。如图1b所示，该曲线由平稳段、陡升段和缓降段组成。在P 波到达前，信号仅由噪声构成，峰度曲线趋于平稳，峰度值为0；随着时窗的移动，信号成分由纯噪声信号向微地震和噪声的混合信号变化，此时，峰度值会随信号成分的变化而发生变化；P 波到达一定时间后，信号成分由噪声与微地震信号的混合信号向纯噪声信号变化，此时体现微地震信号非高斯性的峰度值会逐渐减小，最后趋于0。由上述分析可知，在P波到达附近峰度曲线会发生明显的突变，由此可将峰度曲线的全局最大斜率定义为P震相的初至。图1a中，黑色虚线表示模拟信号P 震相的初至，它与峰度曲线的最大斜率处重合。由此可以看出，峰度法对具有清晰P 震相起跳的微地震信号有很好的拾取效果。

然而，在页岩气开发微地震监测过程中，实测的微地震记录信噪比普遍较低，并常伴随强尾波、尖峰信号，给P震相的初至拾取造成很大影响。图2给出了低信噪比模拟微地震信号及其峰度值曲线。图2a为信噪比为－6 dB 的模拟微地震信号，采样间隔为0.1667×10－3s，P 震相初至点对应第1000个采样点，如图中黑色虚线所示；图2b为微地震信号的峰度值曲线，最大斜率对应第1031个采样点，如图中黑色虚线所示，拾取结果滞后了31个采样点，即延迟了5.1677×10－3s（采样点个数×采样间隔）。由图2可知，对于低信噪比微地震信号，仅使用峰度法拾取P震相初至会带来较大的拾取误差，需要改进其计算对象及过程，以提高拾取精度。

图1 高信噪比模拟微地震信号波形（a）及其峰度值曲线（b）（信噪比为10 dB）

图2 低信噪比模拟微地震信号波形（a）及其峰度值曲线（b）（信噪比为－6 dB）

2 小波多尺度分解及P震相初至拾取

2.1 小波多尺度分解

小波变换作为分析复杂非平稳信号的有效工具，在提高地震资料分辨率和信噪比[20，23]、压缩地震数据[24-25]、表征介质奇异结构[26]、地震资料反演[27-28]等方面均得到了广泛的应用。在微地震数据处理过程中，小波基的选取以及分解层次的设定，均会对信号后续的分析处理产生影响。其中，小波基的选择必须具有对称性才能有效防止地震相位失真[29]，而适当分解层次的设定，不仅能减少计算量，还能有效分离低频信号与高频信号。经过多次数值模拟实验，在微地震数据处理过程中采用db10小波基最为合适，该小波基具有正交性、对称性和紧支撑等特点；分解层次设定为3。

使用db10小波基对微地震信号x（n）进行3层小波分解，如图3所示，可得到尺度空间的近似序列a1，a2，a3和细 节 空 间 的 细 节 序 列d1，d2，d3。其 中近似序列的重构信号对应原信号每层分解的低频部分，细节序列的重构信号对应原信号每层分解的高频部分。为有效凸显微地震信号的主成分，降低高频信号对P 震相初至拾取的影响[29]，本文对近似序列a1，a2，a3进行离散小波逆变换，从中选取合适的重构近似信号用于P震相初至拾取。

图3 小波多尺度分解示意

图4给出了主频为120 Hz的模拟微地震信号（信噪比为－6 dB）及小波多尺度分解后各层低频重构信号。图4a为模拟微地震信号；图4b、图4c和图4d分别为近似序列a3，a2和a1通过离散小波逆变换得到的重构信号A3，A2，A1。从图4可以看出，A1，A2，A3分别是滤除部分高频噪声后的有效信号，但A1、A2中依旧包含较多高频成分，而A3在保持相对清晰的P 震相初至信息的同时，剔除了大部分高频成分。因此，文中将重构信号A3用于后续初至拾取。

为进一步确认上述小波基选择、分解层次设定以及信号选取的有效性，图5给出了合成微地震信号与重构信号A3的时频分析结果。从图5a可以看出，相对于有效微地震信号，噪声信号频率较高。图5b为所选重构信号A3及其时频分析结果。由图5b可见，小波多尺度分解可以实现高频噪声和有效信号的分离，信噪比可以得到极大提高，而且重构信号A3与原始信号的能量信息在时频谱上能保持一致，证明了A3可以代替原始数据进行初至拾取。

2.2 特征函数构建

为进一步提高本文方法的初至拾取精度，重新构建了特征函数序列。常见的特征函数通常包括以下4种[30-31]：

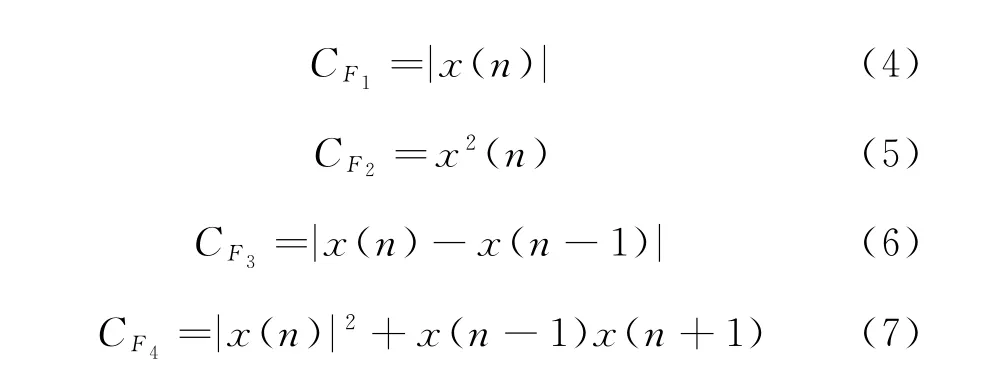
特征函数（4）和特征函数（5）在时域上表现较为突出，体现信号的幅值变化；特征函数（6）和特征函数（7）体现信号的频率变化。LI等[31]指出仅用（6）式作为信号的特征函数时，若背景噪声的频率高于地震信号的频率，则该特征函数无效。因此，特征函数的好坏直接影响初至拾取的结果。为充分反映信号频率与幅值的变化，并兼顾微地震信号的低信噪比和多震相特点，本文构建了如下特征函数：

根据峰度法原理求特征函数序列的峰度值：

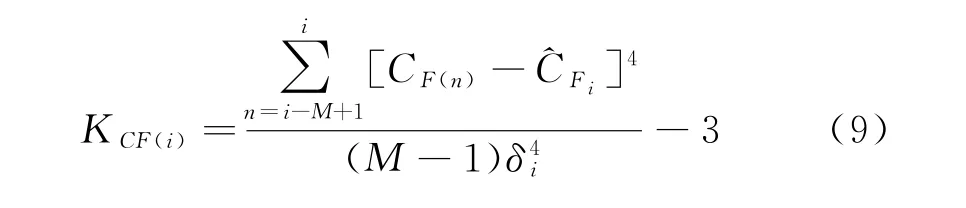
^CFi和δi的表达式为：

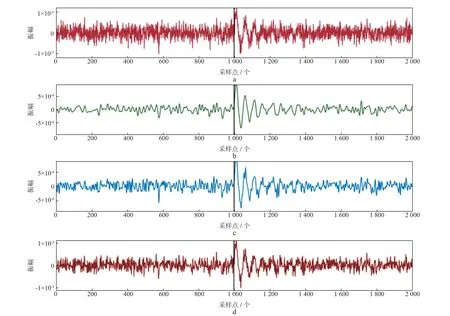
图4 低信噪比模拟微地震信号波形及小波分解后的各层低频重构信号（黑色实线表示模拟信号的初至点）

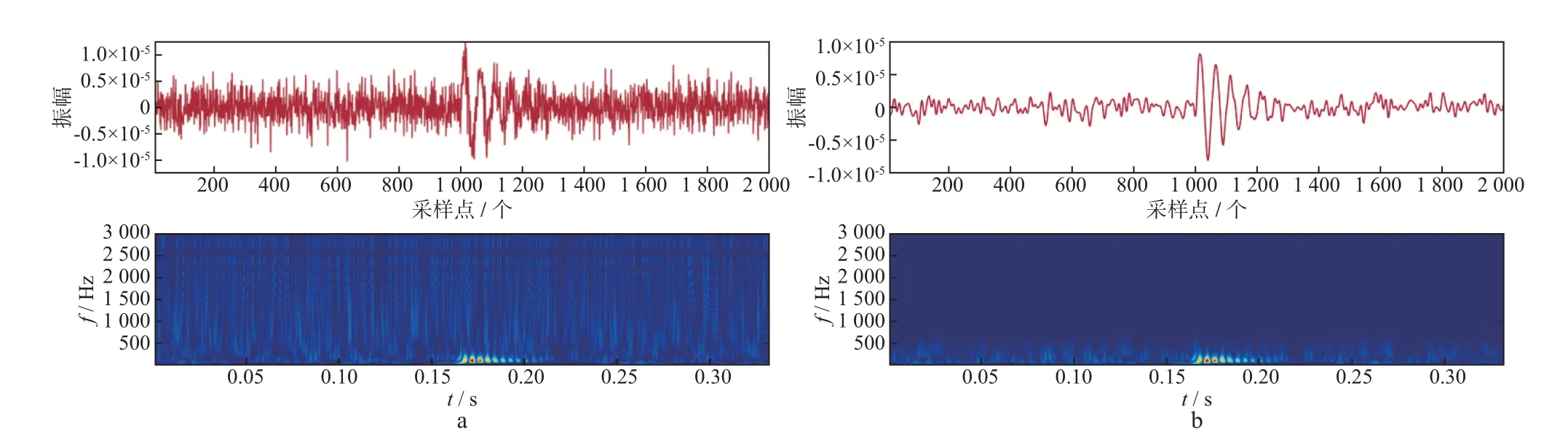
图5 合成微地震信号（a）与重构信号A 3（b）的时频分析结果

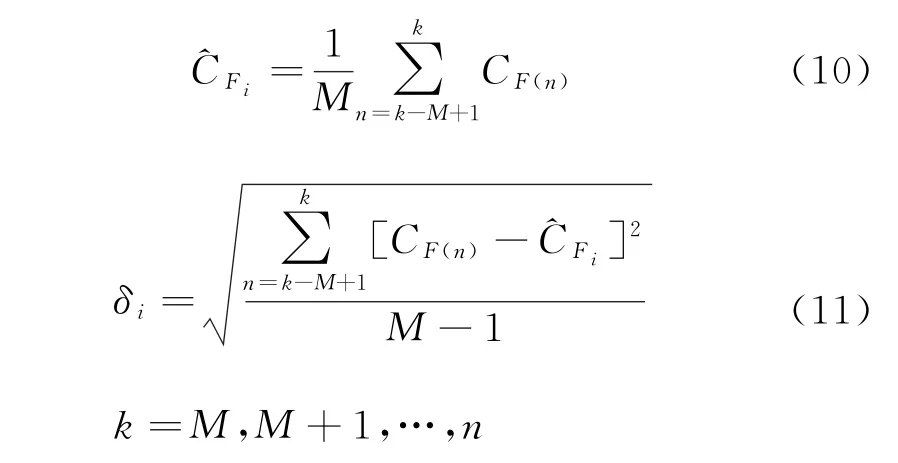
2.3 P震相初至拾取

本文方法的步骤可概括如下。

1）对于低信噪比微地震信号序列x（n），利用小波多尺度分解将其高频噪声与有效信号分离，选取重构信号A3用于初至拾取。其中所选小波基为db10，分解层次为3。

2）通过（8）式构建重构信号A3的特征函数序列。

3）将峰度值计算应用于所构建的特征函数序列，选取峰度值的全局最大斜率作为P 震相初至。其中，时窗的设置对拾取精度和效率有至关重要的影响[20-21]，时窗过长不仅会增加计算量，而且会造成信息冗余，影响拾取精度。经大量数值模拟实验，本文方法的时窗长度设置为200。

图6对比了峰度法、本文方法、小波分解与高阶统计量联合方法[20]对低信噪比（信噪比为－6 dB）模拟微地震数据P震相的拾取结果。图6a为模拟微地震信号波形及上述3种方法的初至拾取结果，图中黑色实线表示预设的P 震相初至，红色实线表示本文方法的拾取结果，绿色实线表示小波分解与高阶统计量联合方法的拾取结果，蓝色实线表示峰度法的拾取结果；图6b为图6a的局部放大图。从图6可以清晰看出，本文方法的拾取效果更好，其余两种方法的拾取误差均大于本文方法。

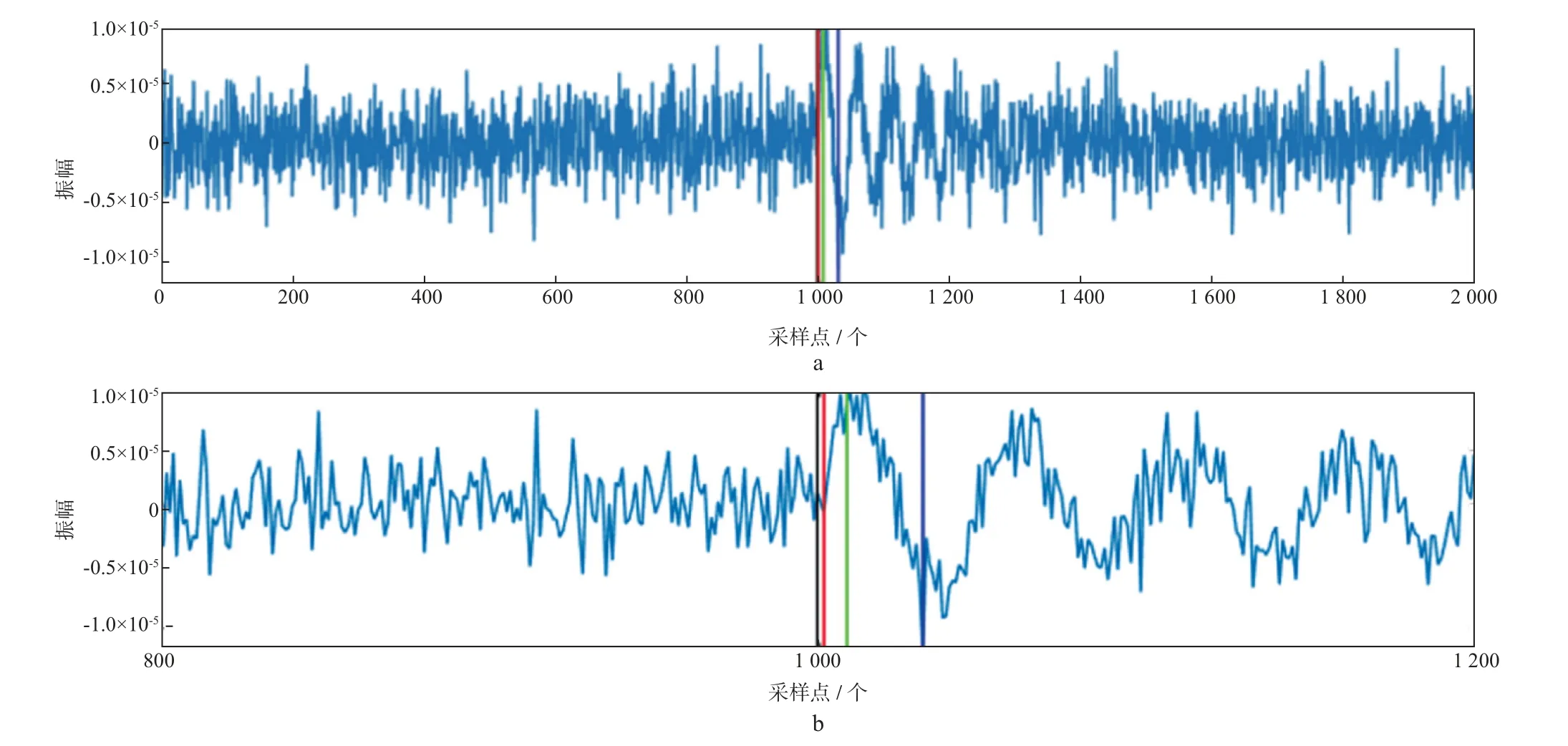
图6 不同方法的模拟微地震数据P震相初至拾取结果（信噪比为－6 dB；P震相初至在第1 000个样点处）

3 应用效果分析

3.1 模拟微地震数据实验

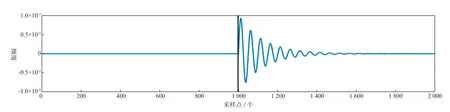
图7 模拟微地震信号（黑色实线表示初至点在第1 000个样点处）

为了验证本文方法拾取P震相初至的可行性和稳定性，分别采用本文方法、峰度法、小波分解与高阶统计量联合方法对模拟微地震信号进行拾取精度与效率对比。图7所示为模拟微地震信号，该信号是由衰减的正弦波产生，主频为120 Hz，采样间隔为0.1667×10－3s，数据长度为2000个采样点，P 震相初至点预设在第1000个样点处。

原始信号与加入噪声的能量比值为信噪比[32]：

式中：T为信号长度；S，N分别表示原始信号与加入的噪声信号。采用公式（12）构造信噪比为－5，－6，－7，－8，－9，－10 dB 的含噪微地震信号，对应每个信噪比值构造1000组模拟微地震信号，分别采用上述3种方法对其进行初至拾取，进而计算相同信噪比模拟微地震信号拾取误差的平均值，结果如表1 所示。对比3种方法的拾取结果可见，本文方法的拾取精度更高。实验表明，本文方法的拾取误差能够控制在0.0302×10－3～1.3002×10－3s。

在相同计算平台上，采用信噪比为－6 dB 的1000组模拟微地震信号对上述3种方法的计算效率进行比较，统计结果如表2所示。由表2可见，相比于传统峰度法，本文方法的计算效率有所降低，这是由于小波多尺度分解与特征函数的构建增加了计算量，时间消耗有所提高。但效率的降低随之而来的是拾取精度的提高。本文方法中小波基选取、分解层次的设定及拾取准则均优于小波变换与高阶统计量联合方法，因此本文方法的计算效率略高。由表1 和表2可知，本文方法相比于小波分解与高阶统计量联合方法在拾取精度和计算效率方面都有所提高。

表1_3种方法对不同信噪比模拟微地震记录的P震相初至拾取误差统计

3.2 应用实例

为检测本文方法的实用性，分别采用峰度法、本文方法对实测微地震记录的P 震相初至进行拾取，并与人工拾取结果进行了对比。

图8给出了采用不同方法对6组微地震信号的P震相初至拾取结果。其中，各图上图为实测微地震记录的振幅-时间曲线，其采样间隔为0.1667×10－3s；下图为实测微地震信号的重构信号A3的局部放大图，图中黑色实线为人工初至的拾取结果，红色实线为本文方法对原信号初至的拾取结果，蓝色实线表示传统峰度法对原信号初至的拾取结果。从图中可以看出，相比于传统方法，本文方法拾取结果与人工拾取结果更为接近。其中，图8a为P 震相初至相对清晰的微地震信号初至拾取结果，由图8a可见，与传统峰度法相比，本文方法的拾取精度提高了1.002×10－3s；图8b、图8c为具有强尾波的微地震信号初至拾取结果，由图8b和图8c可见，与传统方法相比，本文方法可有效克服尾波信号的干扰，图8b中本文方法的拾取精度比传统峰度法提高了12.6692×10－3s，图8c中本文方法的拾取精度比传统峰度法提高了9.0018×10－3s；图8d为伴随有尖峰的微地震信号初至拾取结果，图8d中本文方法的拾取精度比传统峰度法提高了133.36×10－3s；图8e、图8f为受环境噪声影响较强的微地震信号初至拾取结果，图8e和图8f中本文方法的拾取精度比传统峰度法分别提高了7.5015×10－3s和5.6678×10－3s。综上所述，本文方法的拾取结果与人工拾取结果更相近，实现了更准确的P震相初至拾取。

图8 不同方法对6组微地震信号的P震相到达时拾取结果

4 结论

针对页岩气微地震监测资料信噪比低、初至难以拾取的问题，本文提出了一种基于特征函数构建的峰度与小波多尺度分解的P震相自动拾取方法。相比于传统峰度法，该方法既保持了小波分解的多尺度分析特性以及对随机噪声的抑制特性，又克服了传统峰度法对低信噪比、强尾波和尖峰的微地震信号拾取不准确的缺点。将该算法用于不同信噪比模拟微地震信号的测试，并与传统峰度法、小波分解与高阶统计量联合方法进行比较，结果表明，本文方法能够对低信噪比微地震数据的P 震相进行准确拾取，且误差为0.0302×10－3～1.3002×10－3s，具有一定的鲁棒性和准确性。将本文方法应用于实际微地震记录的P震相初至拾取，进一步验证了本文方法的有效性和实用性。本文只是针对P 波初至拾取进行研究，然而，在微地震数据分析过程中仅对P 波进行拾取是远远不够的，适当的S波模型和可靠的S波到达时为震源定位、地震层析成像均提供了重要的约束。因此我们下一步将研究如何实现P波、S波的同时拾取。