基于学习自动机的雷达干扰资源分配研究

韩 鹏，顾荣军，卢俊道，张 鹏

（中国洛阳电子装备试验中心，河南孟州454750）

0 引言

电子对抗过程中双方都会被多部雷达同时威胁，对抗双方会设法利用先进的电子对抗技术削弱对方雷达系统的作战性能。然而雷达干扰资源是有限的，如何将有限的雷达干扰资源进行合理分配，最终获得最大整体干扰效益就成了现代电子对抗中一个决定胜败的重要问题。

正是由于雷达干扰资源分配的重要性，相关专家学者们进行了大量研究，建立了诸多资源分配的方法模型，如基于贴近度的雷达干扰分配算法[1]、遗传模拟退火算法[2]、基于多Agent分布协同拍卖的雷达干扰资源分配算法[3]、蚁群算法[4]等。近年来，博弈论[5]作为研究分布式最优化问题的一种有效理论工具被广泛用于无线通信等领域，取得了很多研究成果，但是在雷达有源干扰资源分配方面研究的不多。本文基于博弈论探讨干扰资源分配问题，并利用学习自动机设计分布式干扰资源分配算法，可以在收敛速度和干扰效果两方面取得较好的平衡，使得对雷达干扰资源分配方案的制定更加稳定和高效。

1 干扰效果评估

雷达干扰资源分配首先需要对干扰机的干扰效果进行定量评估，进而通过运筹学的方法寻找某种最优的干扰目标分配方案。

1.1 评估指标[6-8]

1）干扰频率。用干扰频率效益因子Efij表示干扰机i对目标雷达j的频率瞄准程度对干扰效果产生的影响。设雷达j的工作频率范围为fj1-fj2，干扰机的频率覆盖范围为fi1-fi2，则：

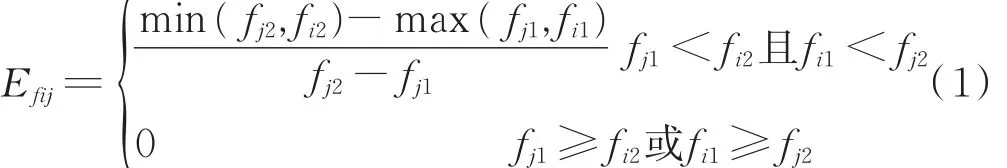
2）干扰功率。用干扰功率压制效益因子E pij表示干扰机i对雷达j的功率压制的程度对干扰效果产生的影响。

式中，Pji表示雷达接收到的干扰功率，Pjs表示雷达接收到的目标回波信号功率，γj表示雷达j正常工作所必需的最小干信比。

3）干扰时机。用干扰时机效益因子E tij表示干扰机干扰实施时间对干扰效果的影响程度[6]。设雷达的威胁时间为t1-t2，开始干扰的时间为ti。

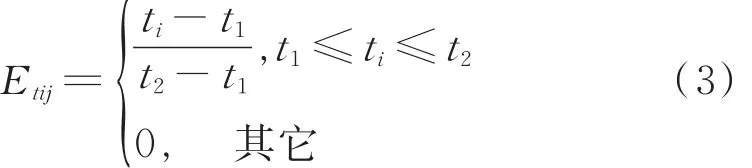
4）干扰样式。用干扰样式效益因子E mij表示干扰机i干扰样式多少对干扰效果的影响程度。

样式越多，匹配程度越高，干扰效果越好。

1.2 干扰资源分配模型

假定己方有N部干扰机，敌方有M个目标雷达。干扰机i最多可同时干扰K i部雷达，各雷达的威胁系数为λj。

影响干扰效果的4个因素是相互独立的，只要其中一个因素无效，干扰就无效。所以在干扰效果综合评价时，采用扎德算子“∧”进行取小运算。

根据电子战的实际战情分析配置权重，用Ω=[ω1,ω2,ω3,ω4]表 示 ，ω1+ω2+ω3+ω4=1。 则单对单雷达干扰效果为：

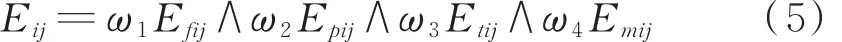
雷达j受到干扰机的干扰效益为：

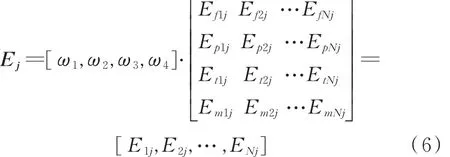
则雷达总体干扰效益矩阵E为：

定义雷达干扰资源分配的目标函数：

2 干扰资源分配博弈模型

假设N个干扰机的集合为N={1,2,…,N}，M个雷达的集合为M={1,2,…,M}。干扰机i的干扰策略为Ri，Ri为干扰机i的干扰策略集，R i∈ Ri。因为干扰机i最多同时对K i个雷达进行干扰，所以Ri=，其中a、b∈ M，因此干扰机i共表示干扰机i对雷达j进行干扰，)表示干扰机i对雷达a、雷达b等K i个雷达进行干扰。干扰机选择不同的干扰策略，就会生成不同的决策矩阵X N×M。假设每一个干扰机都是理性的，只会选择使自身收益最大的干扰策略。定义所有干扰机收益相同，为：

本文以最大化所有干扰机收益为目标，因此干扰策略选择的竞争最优问题可以表示为：

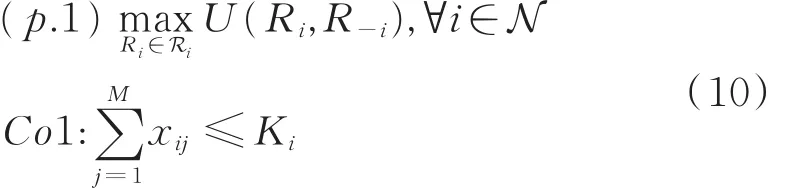
式中，R-i表示除了干扰机i之外所有干扰机的干扰策略，Co1表示干扰机i同时最多干扰K i部雷达。

不满足Co1限制的干扰策略不会被选择，然而干扰机很难提前知道哪些干扰策略是不可行的，所以不能直接采用U作为干扰机的收益函数。为了确定干扰策略选择的可行性，定义每个干扰机的收益函数为：

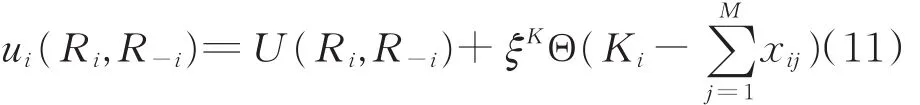
从博弈论的观点来看，N个干扰机构成博弈参与者，干扰策略集构成纯策略空间，干扰机的收益函数构成博弈参与者的收益函数，则干扰机干扰策略选择行为可以被看作是一个博弈GE。

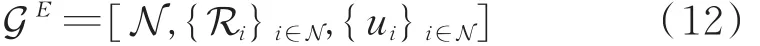
式中，N为干扰机的集合，Ri为干扰机的纯策略空间，ui为干扰机i的收益。

3 基于学习自动机的干扰资源分配算法

学习自动机(LA）是一个能够在随机环境中通过重复地互动从行动集合中找出最佳行动的自适应决策者[9]，学习自动机已经被应用于无线通信等领域。本文根据学习自动机的概念，设计一种分布式随机学习算法，来自适应地更新干扰机的干扰策略。

为了更好地描述这个学习算法，本文把博弈GE扩展到混合策略形式。用p i={p i1,…,p iTi}表示干扰机i的混合策略，其中p ik表示干扰机i选择纯策略k的行动

如果混合策略的博弈是相继轮流进行的，则可以将每个干扰机视为一个学习自动机，将博弈参与者的纯策略视为学习自动机的行动，那么，这个混合策略博弈可以被视作一个由学习自动机构建成的随机博弈。混合策略p i(t)={p i1(t),…,p iT i(t)}可以被当作在时刻t学习自动机i的行动的概率分布，而p ik(t)表示在t时刻，第i个学习机选择第k个纯策略的概率。干扰机i归一化的收益则被视为第i个自动机的反应函数，即r i(t)=αui(t)，其中0＜α＜1，能够保证r i(t)的值落在[0,1)区间。因此可以得到，r1(t)=…=r N(t)=r(t)=αui(t)。

在学习自动机算法中，干扰机通过有限反馈信息，学习到关于干扰策略的概率分布，以便能够最大化各自的收益。如果其中一个自动机即干扰机根据它当前的行动概率分布独立地选择一个行动时，就说这个博弈进行了一次。为了能够获取这个博弈的纳什均衡，干扰机需要重复地进行这个博弈。该算法具体描述如下：

2）迭代重复以下过程：

①在每个时刻t（t＞0），每个干扰机根据它当前的概率分布p i(t)选择一个干扰策略R i，并上传给指挥中心；

②指挥中心根据每个干扰机的干扰策略，更新决策矩阵，计算干扰机i的反应函数r i(t)=。需要说明的是，本文中所有干扰机都具有相同的反应函数，因此这个反应可以很方便的通过指挥中心广播给每个干扰机；

③每个干扰机通过指挥中心的反馈，利用（13）式更新其行动概率分布，其中0＜δ＜1是一个步长参数，i=1,…,N；k=1,…T i。

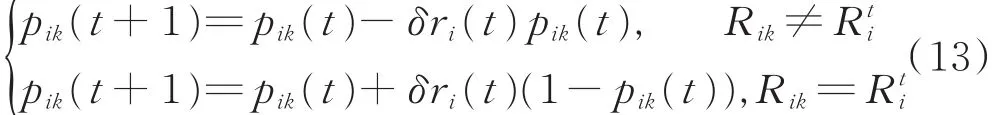
式中Rik为干扰机i的第k个纯策略。

直到p i(t)中存在一个元素近似等于1，比如0.99，算法停止。

分布式干扰资源分配算法，通过重复博弈，最终确定了每个干扰机的混合策略。在任一个时刻，每个干扰机所需要的信息，仅仅是进行了一次博弈后的归一化收益，而不需要知道其它任何信息。所有干扰机只需要计算它们的行动概率，避免了复杂的运算。因此该算法能够极大地降低运算复杂度。

由于GE是一个具有共同收益函数的博弈。由文献[10]中的定理4.1可得，当步长δ足够小时，分布式干扰资源分配算法会收敛到博弈的一个纯策略纳什均衡。当多个纯策略纳什均衡存在时，可以重复运行该算法，然后从中选出获得最高收益的那个纯策略纳什均衡，这样就能直接找到问题p.1的最优解或找到接近最优性能的策略组合。

在传统的学习自动机当中，步长的大小对算法的收敛速度影响很大且是一个预先确定的常数。通常，δ越大，算法的收敛速度就越快。为了能够在保证获得接近问题p.1最优解的情况下，加快收敛速度，本文设计了一个能够自适应调整步长的机制。具体设计如下：

定义一个时变的δ：

式中，t1＜t2＜…＜tn-1是有序正整数，tn被定义为正无限，δ1＜δ2＜…＜δn＜1表示有序步长，n是一个有限正整数。

本文设计的自适应步长调整机制不会影响理论结果。但是，为了能够适应实际需求，必须合理设计这些参数的值。由于自适应步长机制能够把分布式算法的迭代次数自适应地限制在一个需要的数值上，所以这个机制非常适用于实际系统。

4 仿真分析

用仿真实验验证所提算法和模型以及实现方法的正确性。为了对所提算法进行简单高效且全面的分析，首先假设战场环境内有6部干扰机和7部目标雷达，雷达的威胁系数分别为 0.89、0.27、0.64、0.10、0.72、0.43、0.54，每个干扰机最多能同时干扰2部雷达，则每个干扰机的策略数T i=C17+C27=28。通过干扰决策分析，计算雷达干扰效益矩阵Q，计算结果如表1所示。

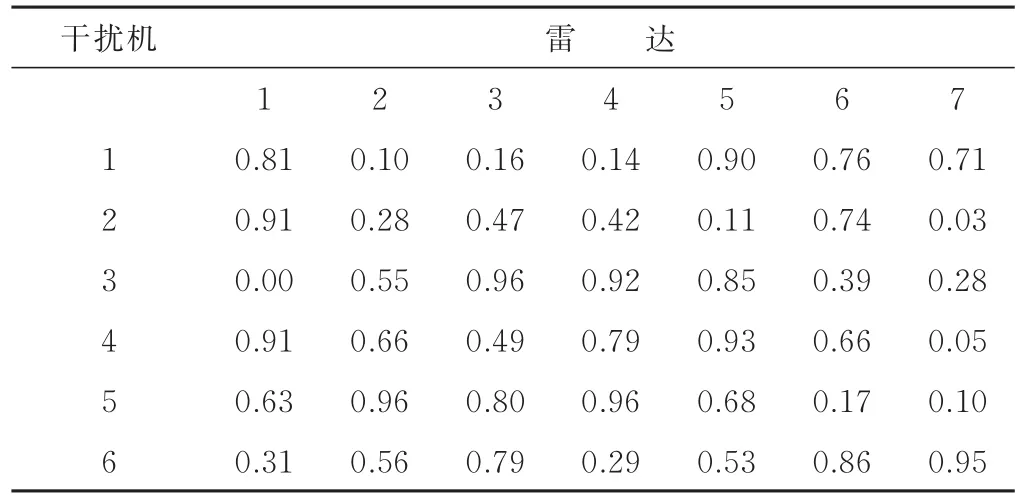
表1 算例干扰效益值

图1表示干扰机1所选行动的概率值（也就是混合策略）的进化曲线。采用自适应步长机制时，n=2，t1=200，δ1=0.1，δ2=0.3。图 1证明本文所设计的算法具有很好的收敛性。

当δ=0.1时，在459次迭代后，干扰机1收敛到策略 5，也就是p15=1，对应的决策矩阵X1=[x11,x12,…,x17]=[1 0 0 0 1 0 0]，即干扰机 1选择第 1个雷达和第5个雷达进行干扰；

当δ=0.3时，在65次迭代后，干扰机1收敛到策略 26，也就是p126=1，对应的决策矩阵X1=[0 0 0 0 0 1 0]，即干扰机1选择第6个雷达进行干扰；

当选择自适应步长机制时，在220次迭代后，干扰机1收敛到策略5，也就是p15=1，对应的决策矩阵X1=[1 0 0 0 1 0 0]，即干扰机1选择第1个雷达和第5个雷达进行干扰。

当δ很大且策略数很小时，算法的收敛速度就会很快。此外，在相同状态下，对于不同数值的δ，分布式干扰资源分配算法可能会收敛到不同的纳什均衡。

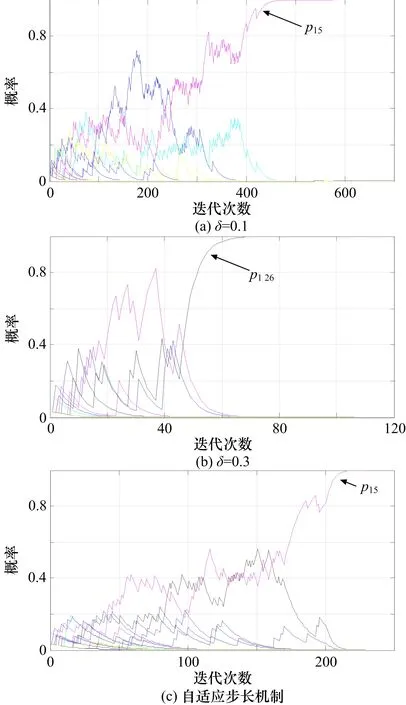
图1 干扰机1的所选行动概率（混合策略）进化曲线

图2 给出了不同算法在不同干扰机数量情况下所获得的干扰效益。图2表明，不论干扰机数量是多少，分布式干扰资源分配算法都能够获得比随机选择算法大得多的干扰效益。如果在仿真中，运行分布式干扰资源分配算法2次并且从中选择一个收益较大的纳什均衡，分布式干扰资源分配算法获得的干扰效益就会得到提升。如果分布式干扰资源分配算法被运行6次，则干扰效益性能会进一步增加。

从图2还可以获知，δ越小，分布式干扰资源分配算法的性能越好。这是由于通常有多个纳什均衡存在，而当δ增大时，分布式干扰资源分配算法更有可能错失最优的或者接近最优的纳什均衡。

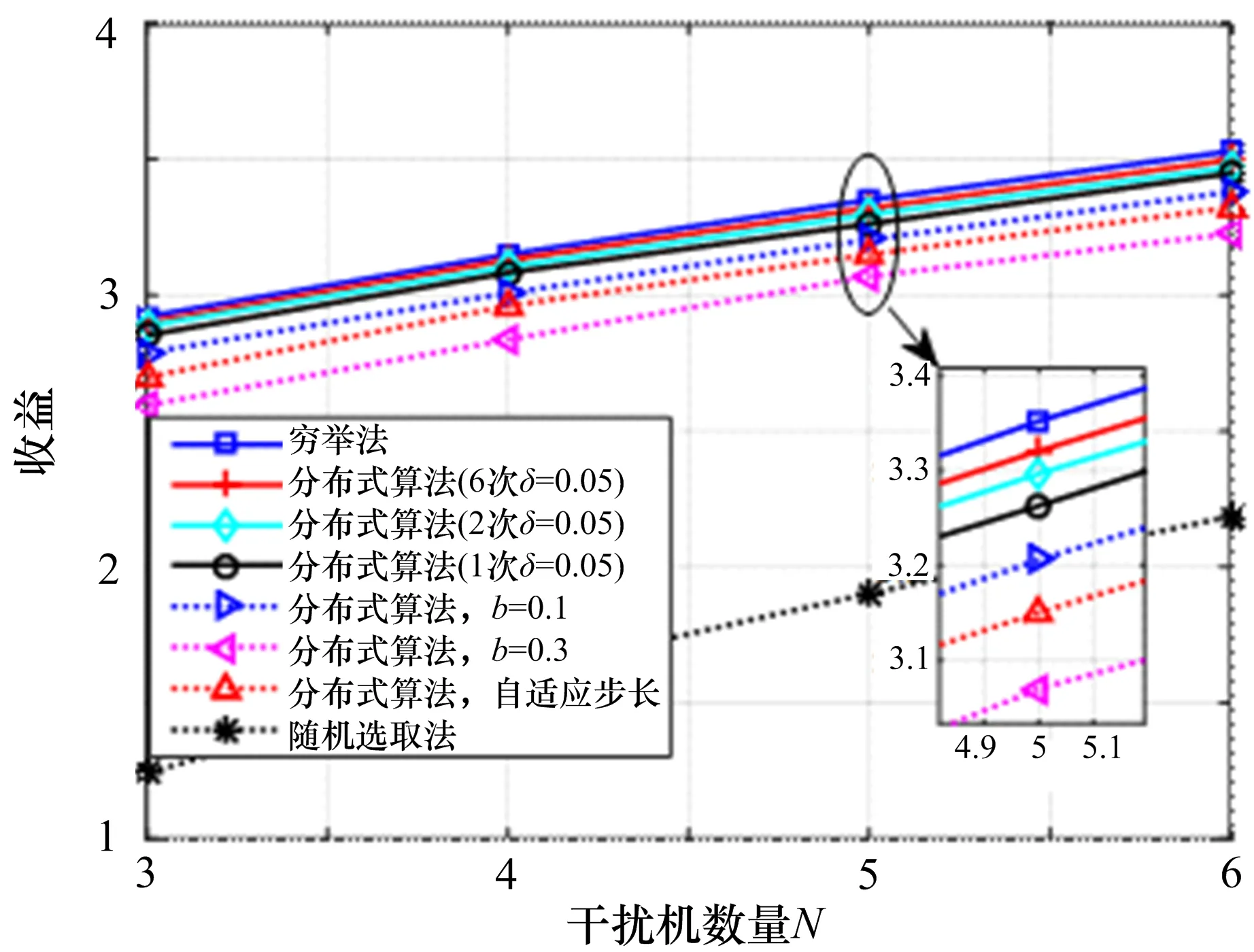
图2 性能对比

图1 和图2表明自适应步长机制能够在干扰效益性能和收敛速度之间获得一个很好的平衡。这些仿真结果证明自适应步长机制是有效的。在实际系统中，可以根据系统需求，来调整步长δ的数值或者采用自适应步长机制来平衡性能与算法复杂度之间的关系。总的来说，分布式干扰资源分配算法灵活有效。

5 结束语

本文利用博弈论研究了雷达有源干扰资源分配问题，基于学习自动机原理提出了分布式干扰资源分配算法，为求解雷达干扰资源分配数学模型提供了新的思路。重复这个算法，可以提高干扰机干扰效益。设计了一个自适应步长机制，它能够平衡算法性能和收敛速度之间的关系。与穷举搜索算法相比，本文提出的算法能够以很低的复杂度来获取一个与之相当的干扰性能。