基于压缩感知的高频雷达目标到达角估计

王 力，赵 丽，齐志平，李 远，李 阳

（1.中国人民解放军95980部队，湖北襄阳441000；2.空军预警学院士官学校，湖北武汉430019）

0 引言

高频雷达（HFR）作为现代空间目标监测、跟踪的重要装备之一，具有系统复杂度高、探测距离远以及识别能力强等特点，其波达方向（DOA）主要通过常规波束形成（CBF）算法实现。然而，基于CBF算法的高频雷达空间目标监测方法存在分辨率低的缺点，因此限制了HFR的方位分辨能力。此外，HFR工作在短波波段，具有电磁干扰过大、外界环境复杂等特点，加之HFR庞大的天线阵列不可避免地会出现部分阵元失效的问题，造成数据干扰过大、缺损的现象。这些问题也是当前基于HFR的空间目标监测、跟踪面临的技术难题。因此，对复杂环境、数据缺损等不利条件下HFR的空间目标DOA估计方法进行研究，对于提升空间目标跟踪技术的发展具有重要作用[1]。针对上述问题，国内外学者已经进行了大量的研究。例如，针对传统CBF算法分辨率不高的问题，已经提出了MUSIC算法[3]、ESPRIT算法[2]等高分辨DOA估计算法[4-5]。而对于HFR，当外界干扰过大、回波数据缺损时，要求算法在短快拍条件下具有较好的估计性能。但是上述算法在外界干扰大、回波数据缺损等条件下均出现性能下降的问题。近年来，众多学者充分利用目标分布的稀疏特征，将压缩感知[6](CS)理论应用到目标DOA估计中，在显著降低数据量的同时提高了DOA估计性能[7-8]。因此，研究基于CS的高频雷达DOA估计方法，对进一步提高短快拍、回波数据缺损条件下的DOA估计性能具有十分重要的意义。

为充分利用CS理论在降低数据量、提高分辨率等方面的优势，本文充分利用HFR观测目标在空间上的稀疏特征，将CS理论与DOA估计相结合，研究了一种基于CS的HFR系统DOA估计方法。首先给出了HFR回波模型，在此基础上构建了基于CS的DOA稀疏表示模型，最后通过相应的CS重构算法实现DOA估计。最终的仿真实验也进一步验证了所研究方法在短快拍、阵列失效等条件下具有估计精度高的优势。本文研究结论对于提高基于高频雷达的空间目标跟踪技术发展具有一定的实际应用价值。

1 HFR回波模型构建

实际上，HFR接收系统可以视为一个具有N个阵元的均匀线阵模型（如图1所示），其阵元间距为d，阵元个数为N。

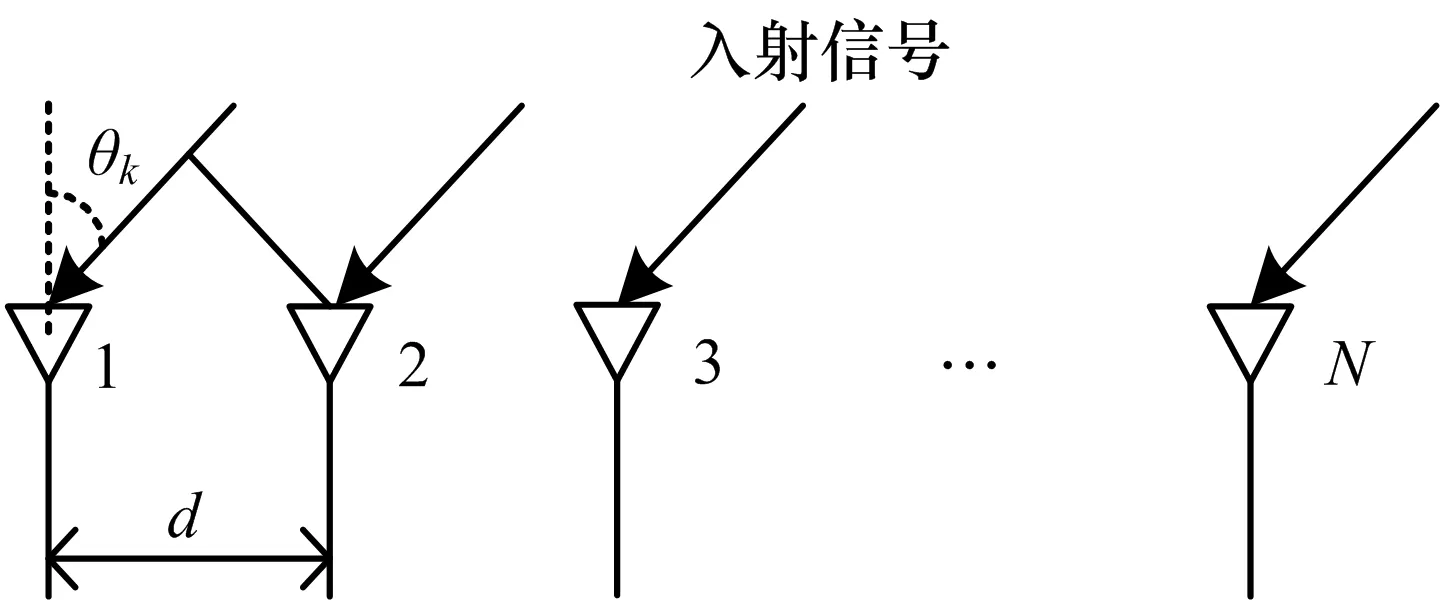
图1 高频雷达接收阵列模型

假设远场有K个窄带信号入射到N(N＞K)个阵元阵列，其波达方向分别为θ1,...,θk,...θK，并以阵列第一个阵元作为基准，则一次快拍下的不同阵元接收信号可表示为：

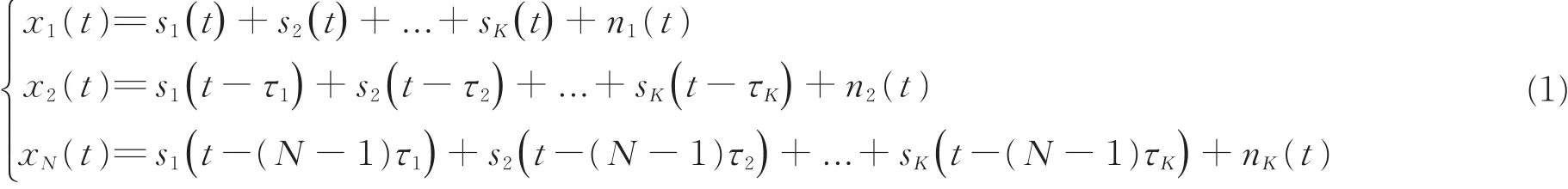
式中，τK为第k个窄带信号的时延，可以表示为τk=dsinθk/c，nk(t)为噪声。

式(1)可以写成：

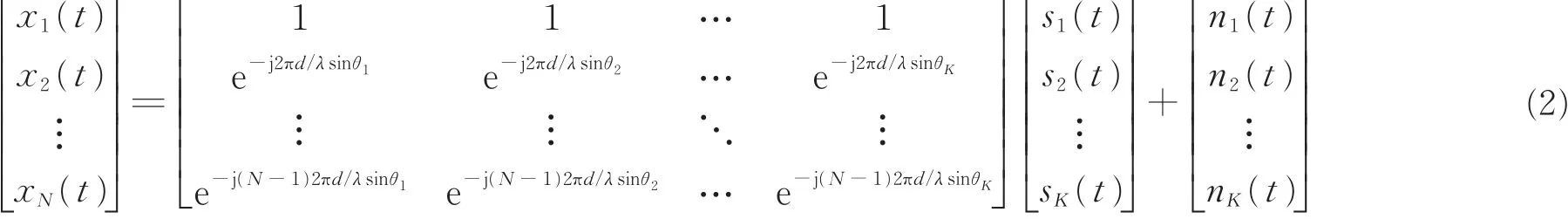
用矩阵可以表示为：

式中，a(θk)为第k个信号的导向矢量，A为阵列流型矩阵，n(t)为噪声矩阵。

2 基于CS的DOA估计方法

CS理论作为一种新的采样理论，主要利用信号的稀疏特性，通过有限的采样数据，采用稀疏重构算法实现对原始信号的完美重构。

2.1 CS基本理论

对于维度为N的复信号x∈CN×1，由信号理论可知，可以将x在一组N×N维正交基Ψ=[Ψ1,Ψ2,...,ΨN]上展开：

式中，Ψn是第n列N维向量，展开系数θn=x,Ψn=ΨTn x，ΨTn表示Ψn的转置。将式(4)写为矩阵形式：

式中，展开系数向量θ=[θ1,θ2,...,θN,]，称Ψ为稀疏基矩阵或稀疏基字典。

根据压缩感知理论，若θ中仅含有K个非零系数或K个远大于其他值的系数（K称为信号X的稀疏度），则可以采用一个与稀疏基Ψ不相关的M×N(M＜N)维矩阵Φ对x进行量测，得到量测值序列y∈CM×1：

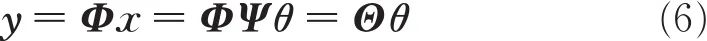
式中，Φ称为M×N维量测矩阵，Θ称为感知矩阵，大小为M×N。若将Θ的每一行看成是一个传感器，那么每一个量测值y都“拾取”了稀疏信号θ所有稀疏值的一部分信息。从y中恢复出原始信号x的过程，称为基于压缩感知的稀疏重构，其相应的重构过程如图2所示。

Candes等人指出[1]：当感知矩阵Θ满足约束等距性（Restricted Isometry Principle，RIP）条件时，信号可以从N个量测值中完美重构。RIP定义为：令index∈{1,2,…,N}，且 |index|≤K。 若 存 在 常 数δk∈ (0,1)对于任意index∈{1,2,…,M}使得式（7）成立：

图2 CS重构原理框图

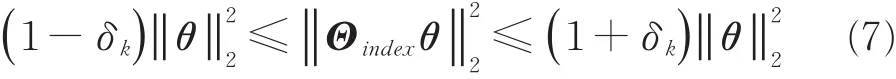
那么称矩阵Θ具有K阶RIP性质，其中使式子成立的最小δ值叫做约束等距常数（RIC），记为δc。

RIP理论提供了一种检验量测矩阵是否可以重构信号的方法，但是判断一个矩阵能否满足RIP条件是非常困难的。因此，文献[2]指出，当量测值个数M与信号维数N以及信号的稀疏度K满足M≥O(KlogN)时，说明低维量测值序列y已包含了准确重构复信号θ足够的信息，这一结论已经成为能否准确重构的标准之一。

当矩阵Θ满足上述条件时，可通过0-范数优化问题来实现对信号θ的重构：

从而可以进一步得到原信号x。目前，已有多种CS重构算法可以实现对式(8)的求解，具体算法实现流程可参考文献[3]。

2.2 基于CS的DOA稀疏表示模型

基于CS的DOA估计的前提条件为信号必须为稀疏的，即观测场景中只包含少量的目标，因此首先需对信号的稀疏性进行分析。对于高频雷达，虽然其观测范围大、探测距离远，观测目标包含飞机、导弹、舰船等，但是均可视为点目标。若将其观测空间划分为P个网格{θ1,θ2,...,θP}（如图 3所示），则探测目标回波信号仅来自于特定的几个网格方向。因此高频雷达目标DOA是稀疏的，可以基于CS理论进行DOA稀疏重构。

假设目标DOA矢量s=[s1,s2,...,sP]，此时对应的DOA估计模型可以视为：

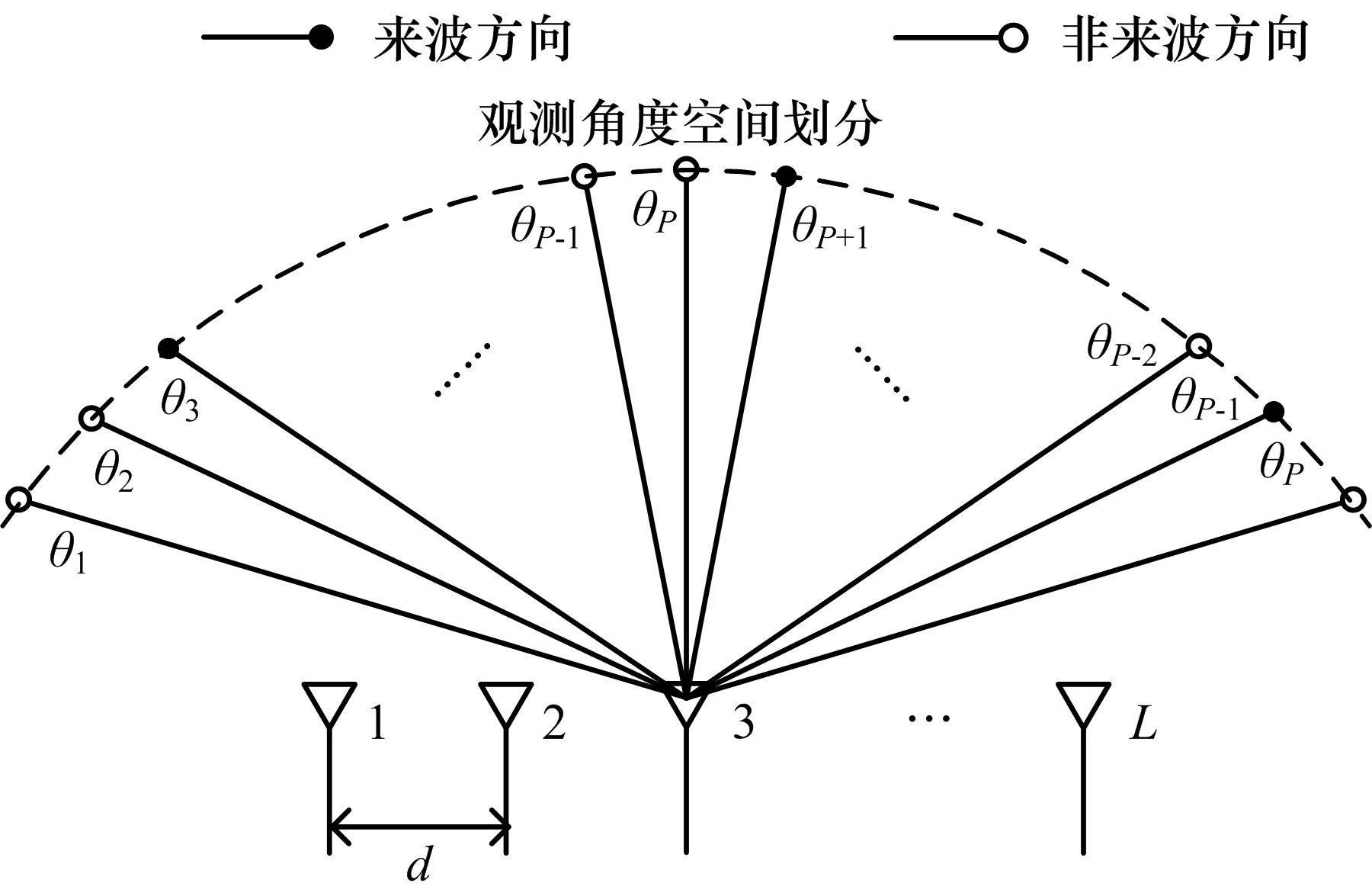
图3 观测角度空间的稀疏划分

式中，x表示一次快拍的回波数据，Ψ为阵列流型矩阵，可表示为Ψ=[φ1,φ2,...,φP]，其导向矢量φp可以表示为：

从式(9),(10)可以看出，阵列流型矩阵中的每一个导向矢量均对应着一个潜在的目标来波方向θp，真实目标的来波方向仅占其中的很小部分，即K≪P。因此，构造的目标DOA矢量s=[s1,s2,...,sP]为K稀疏的，可以基于CS理论进行DOA重构。

假设仅有部分回波数据参与重构，此时相当于对回波数据进行量测，其量测过程可以表示为：

式中，Φ称为M×N维量测矩阵，Θ为相应的感知矩阵。

此时，上述基于CS理论的DOA估计问题可以转化为如下0-范数优化问题进行求解：

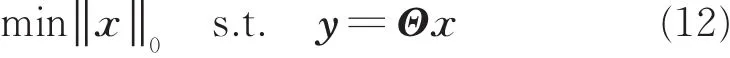
3 仿真分析与验证

假设阵列天线阵元数N为400，阵元间距d为固定值6 m，雷达发射信号载频为10 MHz。雷达观测空间存在三个目标，其来波方向分别为[-30°,0°,40°]。观测空间划分网格数P为 180，范围为[-90°，90°]，网格间隔为1°。为验证所提方法的有效性，本节给出传统CBF算法、MUSIC算法的DOA估计结果作为对比。

3.1 单次快拍条件下的DOA估计结果

首先，分析快拍数对不同方法DOA估计性能的影响。图4为单快拍数条件下，不同信噪比时的DOA估计结果。可以看出，在单快拍条件下，MUSIC方法基本失效，可见其不适用于单快拍条件下的DOA估计。而CBF方法虽然可以在单快拍条件下实现对DOA的估计，但是可以看出估计精度较低，相比较而言，本文基于CS的DOA估计方法具有最高的估计精度，从而验证了所提方法的有效性。

图4 单快拍条件下的DOA估计结果比较

3.2 不同快拍数条件下的DOA估计结果

本节主要研究不同快拍数条件下的估计性能，图5为快拍数分别为128以及256时的DOA估计结果，信噪比设置为30 dB。可以看出，在快拍数较多的情况下，MUSIC方法具有比CBF方法更高的估计精度，且随着快拍数的增大，其旁瓣更低。本文基于CS方法在不同的快拍数条件下均具有较高的估计精度，主瓣宽度最窄，旁瓣水平最低，显示了基于CS的DOA估计方法具有较好的估计性能。

3.3 阵元故障条件下的DOA估计结果

在实际中，高频雷达阵列天线不可避免存在故障、损坏的情况，阵元的故障将会导致DOA估计性能的变化。图6为不同阵元数故障条件下的DOA估计结果，其中故障阵元的位置随机进行选取，信噪比设置为30 d B，快拍数为256。

从图6中的仿真结果可以看出：在10%的阵元故障时，MUSIC方法的估计性能下降最为严重，CBF方法的估计结果其旁瓣增多。当阵元故障数提升到30%时，MUSIC方法基本失效，CBF方法的估计结果其旁瓣进一步增多。而本文基于CS的DOA估计方法在阵元故障为30%的条件下仍然能够得到准确的估计结果。

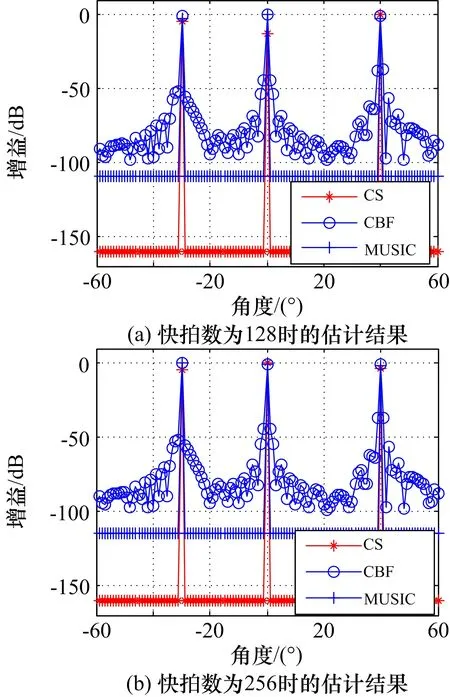
图5 不同快拍数条件下的DOA估计结果比较

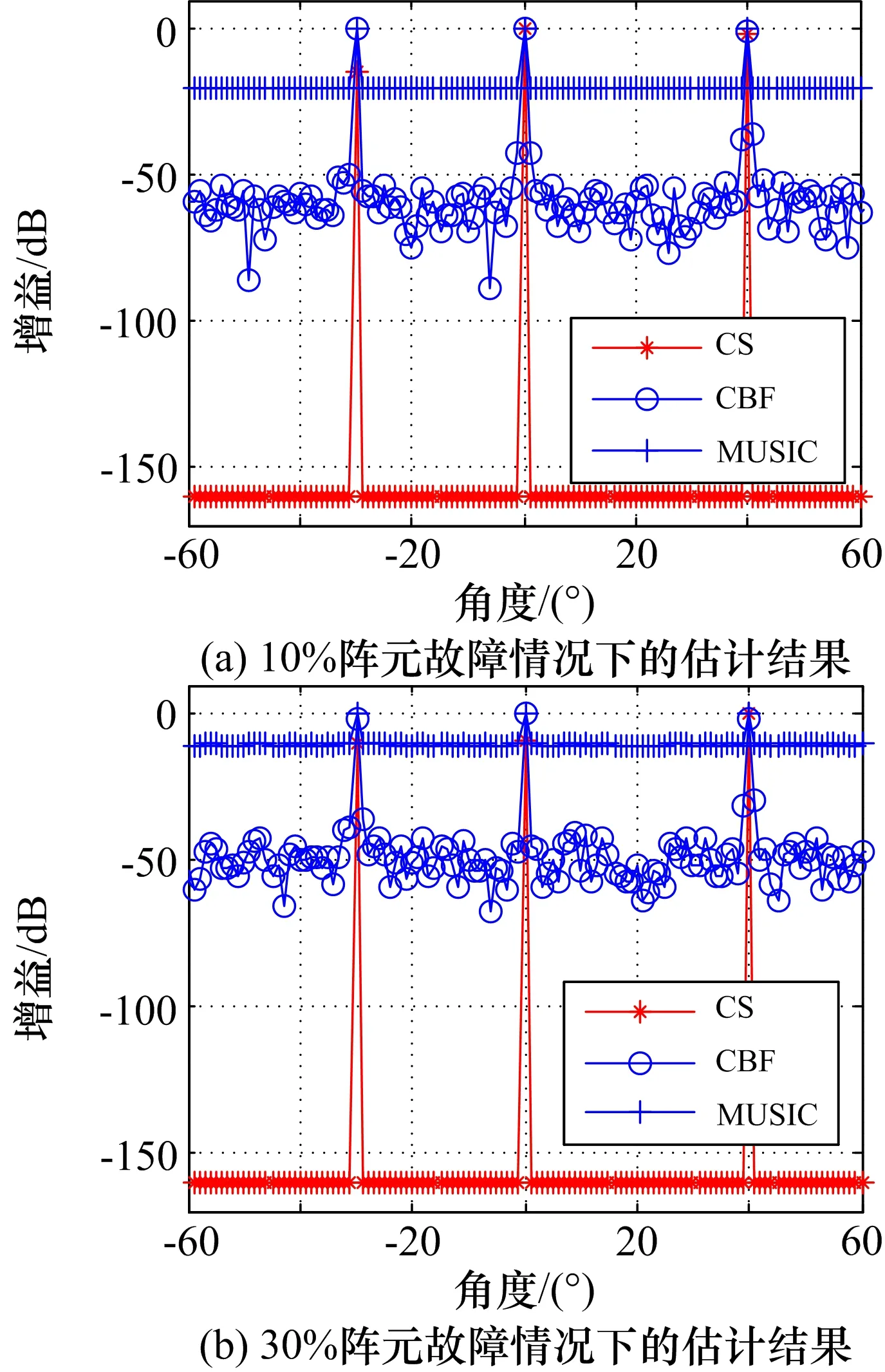
图6 不同快拍数条件下的DOA估计结果比较

4 结束语

本文研究了基于CS的高频雷达DOA估计方法，给出了短快拍（主要指单次快拍）、回波数据缺损条件下的DOA估计性能分析。从文中的分析结果可以看出，基于CS的DOA估计方法具有估计精度高、所需回波数据少等优势。下一步可以将实测数据与所提方法相结合，进一步验证所提方法的有效性。