在课堂教学过程中渗透数学思想方法的策略

冯佳音

在数学教学过程中渗透思想方法，其宗旨是为了能够发展学生的智慧，教学生学会学习。因此，教师在小学数学课上应有意识地渗透一些数学思想方法，以达到提高课堂教学的效率、促进学生思维的灵活性的目的，为学生以后的数学学习打下坚实的基础。数学思想方法是数学学习的“灵魂”，它对知识的形成、发展和在实际生活中的应用起着关键作用。作为数学教师，应该将数学思想方法的渗透落实到教学过程的各个环节之中。

一、在导入新课环节渗透转化与类比思想

数学上的转化与类比思想是指由一类数学对象向另一类与其性质相近的数学对象进行知识的迁移。转化与类比思想方法是帮助学生理解并解决复杂且有一定难度的数学问题。在向学生渗透类比思想的过程中，不仅可以培养他们的想象力、创造力、发散思维能力，还可以促进独立探索研究问题的能力。

如在教学“圆的面积计算”一课时，上课伊始，一位教师通过创设情境来引入新课，他用多媒体出示教材中的主题图，让学生明确所求的草坪面积即是圆的面积。

师：同学们，圆的面积我们马上就要学到了，在学习之前，大家还记得平行四边形、三角形、梯形的面积公式都是怎么推导出来的吗？我们以平行四边形为例。

生：用“割补法”，沿着平行四边形的一条高剪下，将平行四边形分割成两份直角梯形，再通过平移、拼接成长方形来求解。

师：同样的，大家想一想，能否将圆也转化成我们学过的图形来解决这个问题呢？

这样，通过复习用“割补法”把平行四边形转化成长方形来推导平行四边形的面积公式，启发学生思考能不能也利用“割补法”来推导出圆的面积公式。该片断巧用类比的方法，从而渗透了转化与类比思想。

二、在探究新知环节渗透分类和符号化思想

在探究新知这一环节，在教给学生有关数学知识与技能的同时，也要择机向学生渗透分类和符号化的数学思想。

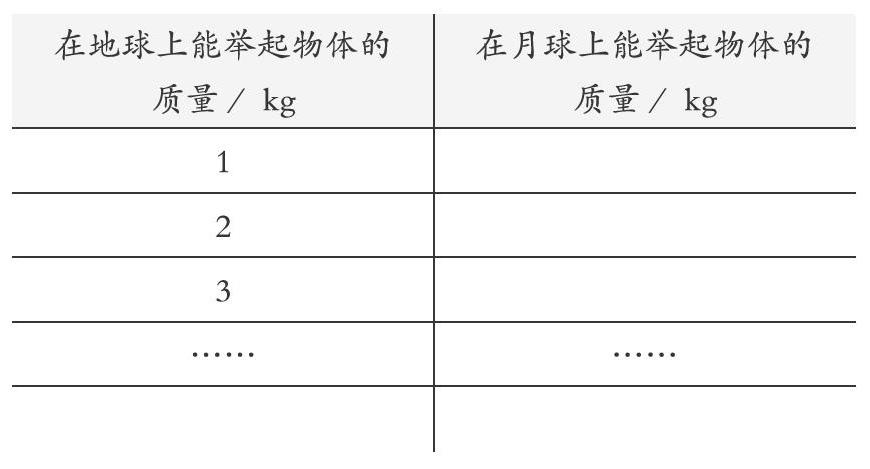
如在教学“用字母表示数”时，可以出示教材中的例题：在月球上，人能举起物体的质量是地球上的6倍，请根据这个信息完成下表。

教学中，可以先通过记录单让学生填表格，这样做可以激发学生自主探索、整理归纳的欲望，让他们根据所填表格数据所体现出来的数量关系进行思考，并用字母和字母式把对应的关系式进行表示。这样，就潜移默化地渗透了分类的数学思想，也提高了学生自主探索和整理归纳的能力。在学生自主探索、合作交流并学会了用字母表示数之后，教师可以再找准时机提问：“为什么是这样表示呢？”从而让学生从具体的问题中抽象出相应的数学关系式，这就渗透了数学符号化的数学思想。如当学生说出在地球上能举起物体的质量用x千克时，可以提问他们x表示什么，这样学生就把数据符号化了。然后，再让学生去说月球上能举起物体的质量时，便有了两者之间的数量关系，学生能发现不管在地球上和月球上能举起物体的质量怎么变，它们之间的数量关系不变。这个发现，也使得符号化思想的本质得以呈现。最后，再与学生四年级时学过的运算定律进行类比迁移，就可以让学生在完善用字母表示数的过程中体会符号化的思想，使知識在不断地对比中越来越清晰。

三、在巩固应用环节渗透数学建模思想

经过探究新知，学生可以感悟和提练到一些数学思想方法，但是要真正将这些数学思想方法转化为数学核心素养，还需在课堂练习中巩固和消化。在课堂练习中，教师在让学生掌握数学知识与技能的同时，也应该充分挖掘学生的潜力，出一些蕴含数学思想的习题，帮助学生建立合理的数学模型，在练习知识与技能目标的基础上，让学生在习题中不但能巩固和消化课堂教学中学到的知识与技能，并且能从习题中体会数学建模的特点和作用，并渗透数学建模的思想。

如在“巧用定律进行简便计算”的巩固应用环节，教师就可以出一道这样的练习：计算125×32×25。学生如果将32分解成8×4，再利用乘法交换律、结合律计算，就显得非常方便。

125×32×25=125×8×4×25

=（125×8）×（25×4）

=1000×100

=100000

运算定律是数学建模的思想方法之一，简便计算是根据算式和数字的特点，由四则运算的性质，在不转变运算最终结果的前提下灵活处理运算过程，从而达到简便计算的目标，二者既有联系又有不同。运算定律蕴含着数学模型的思想，也是学生今后进行数学学习的基础。所以，我们不能把它简单地看成简便计算。教学时，应注意让学生自主探究、合作交流，自然而然地渗透数学建模思想。

四、在回顾小结环节提练数学思想方法

回顾小结是引导学生对数学知识进行系统回顾和整理的过程，是课堂教学的重要环节;但如果回顾小结仅仅是停留在数学知识的归结上，忽视了对数学思想的提练，那么数学教学就会停留于较低的思维层次上。因此，这个环节不但要让学生基本掌握相应的数学知识与技能，还要让他们自己去提练某些数学思想方法，发展相应的数学核心素养。数学知识与技能中往往含有相应的数学思想方法，它们是一个不可分割的整体。在回顾小结时，教师不但要总结数学知识与技能，让学生建立数学知识体系，而且要给学生数学思想方法指导，让学生充分挖掘和提炼数学思想方法。把完整的数学知识与技能的学习和提炼数学思想方法融为一体，才能使培养学生数学素养的目标得以实现。

如在“长方体和正方体的体积”一课的回顾总结环节，教师可以引导学生思考：长方体和正方体的体积计算公式各是怎样推导的？有什么共同点？从而让学生提练概括：在进行长方体体积的计算时，可以应用分割的方法把长方体转化成若干个棱长是1厘米的小正方体来推导，用到了转化的数学思想;在进行正方体的体积计算时，可以应用迁移的数学思想方法把它转化成学过的长方体的体积的方法来推导。这样，学生经过自主提练和生成，深刻体验到可以用转化的数学思想把没学过的数学知识转化为已经学过的数学知识。在这个过程当中，学生理解和掌握了转化的数学思想方法，同时也提升了数学素养。

（责任编辑：杨强）