核心素养下小学数学课堂提问的有效性

林素娟

[摘 要] 课堂提问是沟通教师、教材、学生之间联系的主渠道，数学课堂中教师应当具有提问的技巧，为学生的学习创设好情境。有效地提问，促使学生主动地、富有个性地学习，不断提高发现问题、提出问题、分析问题和解决问题的能力，有效地形成数学核心素养。

[关键词] 小学数学;课堂提问;核心素养

课堂提问是数学课堂中最普遍的教学手段，老师与学生的思想在充满魅力的数学课堂里碰撞、沟通，精心设疑，巧妙发问，让学生主动去探究、发现，激发学生的思维，形成良好的数学核心素养。

一、巧设悬念，提问要“趣”

悬念是学生求知欲动力源泉之一，课堂提问中适时地创设“悬念”，紧扣学生的兴奋神经，引发学生积极思考，通过自己努力自己解决教学中的难点，让他们在探究中尽情享受数学课带来的魅力与乐趣，形成数学核心素养。

例如，在教学“学校教学楼有多高？”时，教师用谈话方式导入新课：“孩子们，我们上课的这座教学楼，你想知道它有多高吗？”同学们七嘴八舌地提了好多种方案都被一一否定，究竟用什么办法最好呢？今天我们将学习一种很有效的解决办法，这时，孩子们都迫不及待地想知道到底是什么方法，自然地导入新授课《用正反比例解决问题》。

数学课堂上用悬念引入新课，学生一下子就会被问题所吸引，马上激起学习新知识的强烈兴趣，大家带着疑问来探索和研究，会收到事半功倍的学习效果。

二、紧扣目标，提问要“准”

课堂提问是教师引领学生启动思维、理解知识的本质特征、实现教学目标而采取的双边活动。这就要求我们要根据教学目标设计准确的问题，让每一个问题紧扣教学目标。

例如，四年级下册《认识平均数》开课之前创设这样的情境：明明和亮亮来到游泳池，游泳池边立有警示牌：平均水深110厘米。

明明：我身高1.05米，不会游泳。

师：明明游泳有危险吗？

生1：没危险。

生2：有危险。

大家争论不休。

师：今天学了这节课，我相信你们会给明明一个清晰的答案。

这样，就能把本节课的重、难点预设在这个轻松快乐的情境中了，孩子们为了给明明一个满意的答复，听课一定会全神贯注。新课后，孩子们最后终于发现了明明游泳没危险，此刻教室里洋溢着胜利的喜悦。

又如教学《分数的基本性质》时，可以讲“小花猫过生日分蛋糕”的故事：小花猫过生日了，他的好朋友小兔、小狗、小熊前來祝贺。猫妈妈要把两块蛋糕分给他们。其中1/2块分给小花猫，2/4块分给小兔，4/8块分给小狗，8/16块分给小熊。这时，小花猫不高兴了，说：“妈妈您不公平，为什么分给他们的多，给我少？”同学们，你们说，兔妈妈这样做公平吗？设计这样的问题，使学生马上进入主动探索学习中。学生纷纷跃跃欲试，积极思考：有的说公平，有的说不公平。这就为探究新知奠定了良好的基础。

在知识重点、理解疑惑、思维转折、规律探求时，精准、恰当、切中要害地提问，使他们处于最佳的心理状态，这样教师也能更好地驾驭课堂，有效地提高数学核心素养。

三、激发思考，提问要“活”

课堂提问是实现师生互动的重要手段，课堂上教师把问题抛给学生，引发学生多角度地横向互动，最大限度地尊重学生的学习潜能与智慧，为他们发散性思维提供平台，给数学课堂增添魅力。

例如，教学《梯形的面积》推导，因为有了之前学习的梯形概念，学生很轻松地操作，将事前准备好的两个全等梯形，一正一倒拼在一起，组成一个平行四边形，如图①。在学生操作后教师提问：你是怎样操作的，得到什么样的结论？学生描述：

①平行四边形的底是梯形的上、下底之和。

②平行四边形的面积=底×高。

③得出：梯形面积=（上底+下底）×高÷2。

这时教师继续引导，鼓励学生第二种操作方法，提问：谁还有不同想法、做法？课堂活跃起来了。也可以用一个梯形通过割、拼的方法，转化成平行四边形。教师问：你是怎样操作的，得到什么样的结论？

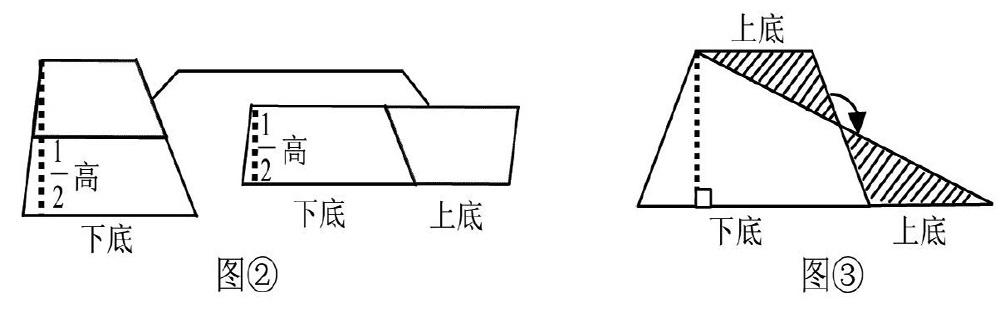
通过学生如图②操作可以清楚地推导出：梯形面积=（上底+下底）×高÷2。

师：这种方法合理吗？得到认可后，鼓励学生第三种推导方法，提问：还有更棒的推导方法吗？通过对一个梯形的割、补，转化为三角形，再问：你是怎样操作的，得到什么样的结论？

如图③，三角形的底为梯形上、下底的和，高相当于原梯形的高。得出梯形面积公式：梯形面积=（上底+下底）×高÷2。

师：大家在探究的推导三角形面积的办法还真多，那你感觉哪种办法最棒？最有创新？

上例中，学生学习方式转变关键在巧妙地提问。教师把握时机，不断提出激发求知欲的问题，充分挖掘孩子潜力，为他们创造展示聪明才智机会，不断提高学生的核心素养。

四、循序渐进，提问要“有序”

学生的思维是从问题中来又到问题中去，始终和问题紧紧相连。所以数学课堂提问应遵循合理的顺序，课堂提问要从易到难，形成梯度，面向不同层次的学生，形成一连串的问题链。这样让学生有顺序地思考，核心素养一步一个台阶走向新高度。

例如，教学《圆的周长》，为了明确周长和什么因素有关，教师循序渐进地提出以下几个问题。

问题一：用什么办法能得到圆的周长呢？学生回答以下两种情况：①滚动法;②绳绕法。

问题二：圆的周长和什么有关系？

教师请同学们用圆规在练习本上随便画一个圆，边画边想，用手指出圆的周长，再画一个圆，要求比第一个圆的周长长，你怎么画的？老师有意识引导学生观察与感受，学生有了亲身经历与体验，就会感受到圆周长和直径有关。

问题三：所有圆的周长都是直径的3.14倍吗？这个倍数是怎么知道的呢？

教师激发了学生探究的愿望，通过测量来计算圆周率。教师提示学生用“毫米”做单位，圆的周长和直径分别测量三次，把测量结果汇报出来，但不要求算出周长与直径的比值，把计算交给电脑。学生汇报：

生1：周长221毫米，直径71毫米。

生2：周长218毫米，直径70毫米。

生3：周长209毫米，直径64.7毫米。

生4：周长87.5毫米，直径24.6毫米

……

问题四：观察一下我们亲手得到的这些数据，你有什么想法？为什么同一个圆，每次测量的长度会不尽相同？

这样，教师通过一组从易到难，由浅入深，层层相扣的提问，不断地引导学生经历探索圆周率的过程，感受数学思想，达成教学目标。要实现有效教学目的，教师就应勤思考，多分析，努力优化课堂教学，“问”出学生的思维，“问”出学生的激情，“问”出学生的创造。

总之，课堂提问是一门艺术，是培养小学生数学核心素养的重要路径。教学中，教师要联系学生实际，不断挖掘教材，课堂上根据实际情况把握时机，精心设疑，巧妙发问，充分调动学生的积极主动性，有效地渗透数学核心素养，真正实现学生的全面发展。

[参 考 文 献]

[1]肖雪媛.掌握“提问”技巧，焕发“课堂”精彩[J].福建基础教育研究，2015（9）.

[2]黄献串.以适切性问题引导团队高效互动[J].福建教育，2015（6）.

（责任编辑：李雪虹）