引发数学分类讨论的线索刍议

李超 景敏

[摘 要] 在已有分类讨论思想方法研究的基础上，着重对分类讨论的题目进行分析，从中归纳出引发分类讨论的线索是题目中存在的不完整或不全面的数学信息。

[关键词]  初中数学;分类讨论;原因分析;思想方法

众所周知，数学思想方法是数学的灵魂。在很大程度上说，如果掌握数学思想方法，就能够在解决综合性问题时以不变应万变。在初中阶段，分类思想方法是常见的数学思想方法之一，不仅渗透在数学知识生成的过程中，也存在于数学问题解决的过程中。它能够把难于理解的数学知识变得明朗，复杂的数学问题变得简单。由此可见，在解决问题的过程中，运用分类思想方法进行分类讨论，既是一种重要的教学思想，也是一种重要的解题策略。

所谓分类讨论思想方法，是指从所研究的数学对象出发，按照其本质属性的相同点和不同点进行逻辑上的划分，一般将数学对象划分成若干个不同种类，然后分别对划分的这几类情况进行讨论研究，从而达到解决问题的一种思维方法。

在运用分类讨论思想方法解决数学问题的过程中，学生经常出现这样的问题：（1）对于某些应该运用分类讨论思想方法来解决的问题，由于学生知识水平有限，思考问题不全面，因此，想不到运用分类讨论思想方法来解决问题。（2）即便是想到运用分类讨论的方法，由于不知道怎样分类，即分类标准不清晰，从而导致解答不完整。究其原因，是学生在解读已知条件时没有注意到分类讨论的线索，即需要进行分类讨论的信息。

笔者查阅了近10年来相关文献，了解到多数学者针对分类讨论的概念、目的、分类标准、分类步骤等做了大量研究，但对于数学问题中引发分类讨论线索的研究相对较少，且尚不够系统。在此背景下，本文以分类讨论思想方法的概念界定为基础，结合分类讨论思想方法的研究成果，着重对数学问题中引发分类讨论的线索做进一步研究，并对在数学教学中如何渗透分类讨论思想方法提出建議，敬请同仁斧正。

一、代数问题中分类讨论的线索

（一）由概念或性质引发的分类讨论

例1 [x2+k-1x+9]是完全平方式，则k=__________。

分析：对“完全平方式”的概念掌握是解题关键。完全平方式应包含“和的平方”与“差的平方”两种情况，即一次项系数存在正、负两种情况。因此，需要对（k-1）的符号进行分类讨论。

例2 若[ab≠0]，求[aa+bb]的值。

分析：解决此问题的关键是要去掉绝对值符号。若去掉绝对值符号，则需要依据绝对值性质判断[a，b]是负数还是正数。但由于已知条件只有[ab≠0]，且无法从中推演出[a，b]是正数还是负数。为了去掉绝对值符号，需要对[a，b]的符号分别进行讨论。

（二）由待定系数的不确定性引发的分类讨论

例3 已知方程[m2x2+（2m+1）x+1=0]有实数根，求[m]的取值范围。

分析：根据所给方程可知，二次项系数和一次项系数均含有字母[m]，但题中并未说明[m]是否为0，因此，无法确定该方程是一元一次方程还是二元一次方程，由此引发分类讨论。

例4 解关于[x]的一元一次不等式k（x-2）>2k-4。

分析：按照解不等式的步骤可得kx>4k-4。根据不等式运算性质可知，不等式两边同时乘以或除以同一个正数，不等号的方向不变，反之，改变。然而，题目中并没有明确说明k是正数还是负数，因此，需要对k的取值范围进行分类讨论。

二、几何问题中分类讨论的线索

（一）由几何概念不明确引发的分类讨论

例5 若等腰三角形中有一个角等于50°，则这个等腰三角形的顶角度数为（  ）

A.50° B.80° C.65°或50° D.50°或80°

分析：虽然题目的已知条件指明了三角形是等腰三角形，且其一个角为50°，但并没有说明该已知角是顶角还是底角，因此，需要对已知角进行分类讨论。

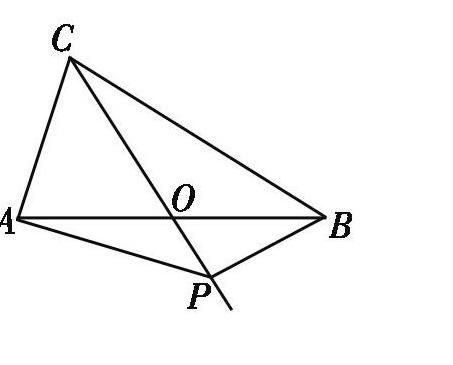
例6 如图，在[△ABC]中，[AB=BC=8，AO=BO]，点[P]是射线[CO]上的一个动点，[∠AOC=60°]，则当[△ABP]为直角三角形时，[AP]的长为多少？

分析：从题目的已知条件来看，没有说明[Rt△ABP]的哪一个角为直角，因此，所给出的已知条件不明确，需要根据图形运动的情况进一步分析。因为点P为射线CO上的一个动点，所以[∠BAP?]不可能为直角。因此，分为两种情况：（1）[∠APB=90°?]，该情况下又可以分为两种可能，点[P]在[AB]的上方或点[P]在[AB]的下方;（2）[∠ABP=90?°]。

（二）由几何图形之间的相对位置不明确引发的分类讨论

例7 已知☉O的直径是2cm，过点A有两条弦AC=[2]cm，AD=[3]cm，则∠CAD的度数是________。

分析：已知条件中没有明确指出前两条弦的位置，即圆心在两弦夹角内还是夹角外，因此，需要对两条线的位置进行分类讨论。

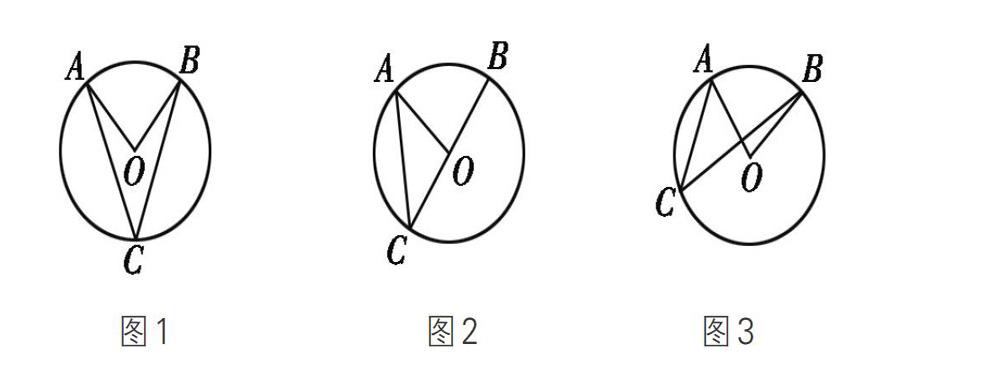
例8 已知[∠C]是弧[AB]所对的圆周角，[∠AOB]是弧[AB]所对的圆心角。求证：[∠C=12∠AOB]。

分析：本题是北师大版初中数学教材中圆周角定理证明题。教材中通过引导学生根据圆周角与圆心的位置关系进行分类讨论。为什么要进行分类，这是解决这道问题的关键。可以引导学生思考：弧[AB]所对的圆周角是不是仅有一个？还可以画出其他的吗？教师通过问题一步步引导学生，得出弧[AB]所对的圆周角有很多个。这样我们就需要对不同的情况进行分类，从而来解决这道题。探究出的三种情况，如下图：

因而，这道题也就迎刃而解了。

（三）由几何图形的形状不确定引发的分类讨论

例9 在?[ABCD]中，[AD=BD]，[BE]是[AD]边上的高，[∠EBD=20°]，则[∠A]的度数为____。

分析：该题目没有给出图形，需要学生自己画出图形。由于没有明确?[ABCD]中哪一组边长，哪一组边短，因此，就有两种可能性。根据题意分析可知，点[E]的位置不确定，导致平行四边形的形状不确定，因此，可以得到两种情况，如下图：

结论

在代数或几何问题解题中，运用分类讨论的主要线索如下。

（1）题目中关于某一概念的信息不全面或不完整时，需要分类讨论。比如，例6中没有指明[Rt△ABP]中哪个角为直角。因此，每个角都可能是直角。

（2）题目中的某一概念还存在多个下位概念时，需要运用分类讨论。比如，例1中完全平方公式包括两个下位概念，一个是完全平方和公式，另一个是完全平方差公式。所以，需要分类讨论。

（3）题目中某一概念呈现形式不唯一时，需要分类讨论。比如，例9中没有给出平行四边形[ABCD]的具体形状，即哪一组对边较长，哪一组对边较短，所以，图形基本形状不唯一。

（4）题目中图形之间的位置关系不唯一时，需要分类讨论。比如，例7、例8中图形之间的位置关系有多种可能，所以需要分类讨论。

[参 考 文 献]

[1]郭秀群.例谈分类讨论思想在初中数学解题中的应用[J].中学数学研究，2017（3）.

[2]侯清乐.初中分类讨论思想在解题中的应用探讨[J].中国校外教育，2016（16）.

[3]姬梁飞.论分类讨论思想方法[J].基础教育，2017（373）.

[4]纽曼曼.初中数学分类讨论思想在解题中的应用探讨[J].教育现代化，2016（8）.

[5]陈罗九.浅谈初中数学中的分类讨论思想[J].中国数学教育，2011（12）.

[6]杨其超.分类讨论思想方法在初中数学教学中的渗透[J].科学素养教学设计，2017（27）.

（责任编辑：赵晓梅）