仿生弯管的冲蚀磨损分析
朱鸿翔
(中石化四机石油机械有限公司,湖北荆州 434023)
0 引言
油气运输管道中含有许多的固体颗粒不断冲蚀着管道内壁,使得管道越来越薄,直至管道破裂穿孔,而对于弯管来说,冲蚀更加严重。因此为了增加弯管的使用寿命,国内外研究人员提出很多种解决方案。SONG等[1]通过研究证明在直管段内壁处建立一定数量肋条可有效的减小壁面的磨损率。FAN等[2]在弯管弯经处的内壁按照一定比例建立一定形状的肋条,并运用有限元仿真计算得到该方法能够有效降低弯管内壁的冲蚀速率。季楚凌等[3]通过建立不同仿生内壁加厚弯管模型,借助于数值模拟计算最终得出仿生表面可以减弱颗粒的冲击动能,其中横槽形内壁弯管较其他种弯管的耐磨性最好。孙鸿志[4]将贝壳耐冲蚀磨损机理应用到弯管内壁,通过仿真计算以及实验验证表面横槽形弯管中肋条可以有效降低颗粒冲击弯头壁面的速度,最后通过极差分析得到抗冲蚀性能最强的仿生弯管。上述方法都是在壁面布置各种形状的肋条来改变固体颗粒的运动轨迹从而降低冲蚀速率,但这些研究对于肋条的形状研究还较少。
本文以油气运输中常用的90°水平弯管为研究对象,重点分析采用仿生形态后弯管冲蚀磨损性能的改变情况。由于材料加工以及现场试验非常困难,仿生技术还没能应用于实际当中,但近些年,国内外很多相关领域专家学者们的研究表明,采用数值模拟技术可以有效预测各类弯管的冲蚀磨损情况。因此,本文将采用数值模拟方法,通过改变肋条的形状来进行对仿生内壁弯管的耐磨性研究。
1 仿生弯管三维模型
以油气运输管道中常用的90°弯管为研究对象,根据文献[4]中说明横槽形仿生弯管可以改善冲蚀。本文以仿生弯管的肋条形状为研究对象,通过改变圆心至流道壁面的距离x(下文称偏心)来改变肋条形状。仿生弯管肋条几何模型如图1所示,x取值 为 0 mm、0.125 mm、0.25 mm、0.375 mm、0.5 mm、0.625 mm、0.75 mm(正常弯管)。通过Solidworks建立相应的物理模型,图2所示为仿生弯管的结构模型,内径为26 mm,入口管段和出口管段均为78 mm,弯曲半径为38mm,肋条直径为1.5 mm,共10个肋条。
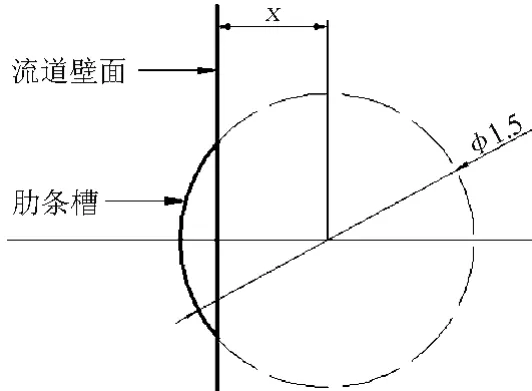
图1 仿生弯管肋条几何模型
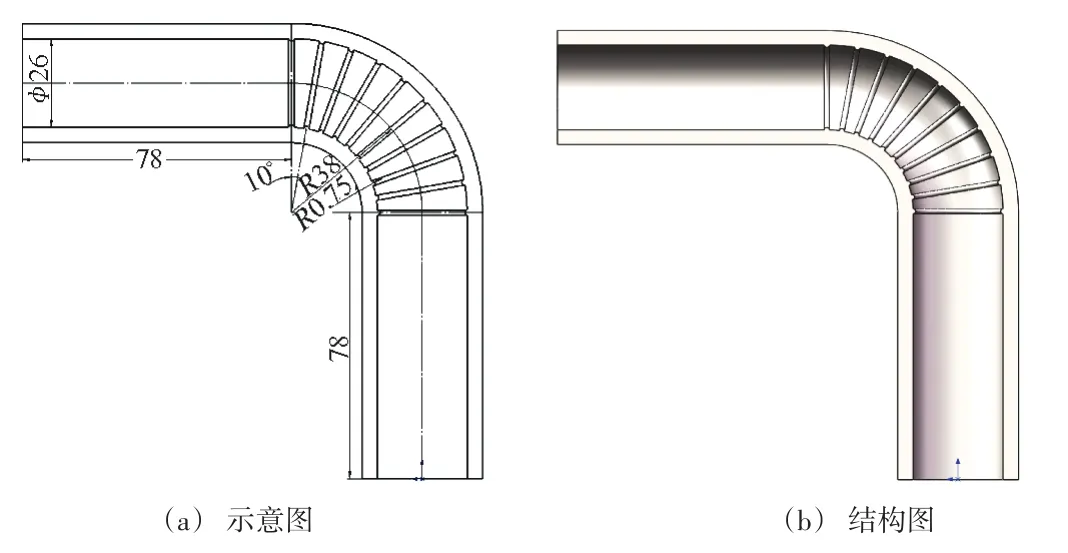
图2 仿生弯管的结构模型
2 数值模拟
2.1 连续相介质及固体颗粒
连续相介质为常温水,为不可压缩流体。离散相砂粒密度设置为2 650 kg/m3,颗粒直径为0.5 mm,砂粒为非球体,形状因子为0.75。
2.2 液固两相流场数学模型
2.2.1 离散相颗粒轨道计算模型
Fluent中的离散相模型(DPM)忽略颗粒之间的碰撞作用,只考虑流体与固体之间的相互作用。其颗粒的运动方程为[5]:

式中:up为颗粒速度,m/s;u为携砂液速度,m/s;FD为固体颗粒受到的力;gx为重力在该方向的分量,m/s2;ρ为携砂液的密度,kg/m3;ρp为粒子的密度,kg/m3;Fx为单位质量颗粒在x方向受的其他力。
2.2.2 冲蚀模型
Fluent将冲蚀分为3个阶段:(1)流体运动带动颗粒运动,计算出作用力;(2)对颗粒运动、碰撞进行分析,得到其轨迹;(3)由材料表面的冲蚀分布及损失质量,计算出冲蚀率的大小。Fluent液固两相流管道冲蚀的参数包括有颗粒直径、颗粒速度和颗粒质量流量,冲蚀率定义为单位时间和面积下金属材料损失的质量,其冲蚀速率的计算公式[6]为:

式中:R为内壁面冲蚀率,kg/(m2·s);N为撞击颗粒数;mp为颗粒质量流量,kg/s;C(dp)为颗粒直径系数,常取值为1.8×10-9;α为颗粒对壁面的碰撞角;f(α)为冲击角的函数;v为颗粒相对速度,m/s;b(v)为相对速度系数,取值为2.6;A为壁面单元面积,m2。
2.2.3 湍流模型
常见的湍流模型共有7类。其中,标准k-ε模型使用最为广泛,是用于计算充分发展的湍流(即雷诺数值范围较高),通过湍动能耗散率ε与湍动能k进行描述的双方程模型。由于湍流的各向异性,其黏性系数也是各向异性张量,而标准k-ε模型黏性系数为各向同性标量,因此,在计算旋转、弯曲流动等情况时,标准k-ε模型会产生误差。为此,在标准k-ε模型的基础上,Realizable k-ε模型应运而生,该模型适合的流动类型比较广泛,包括有旋均匀剪切流、自由流(射流和混合层)、腔道流动和边界层流动。对以上流动过程模拟结果都比标准k-ε模型的结果好。本文研究的仿生弯管中的冲蚀模拟中,管汇中存在多个迂回转折的特点,因此选用计算精度高的Realizable k-ε湍流模型。
2.3 壁面碰撞恢复系数
离散相颗粒与壁面发生碰撞时,碰撞前后速度分量的比值通常被定义为恢复系数,速度分量的变化体现了能量转移和能量损失的存在。2001年,Wallance[7]通过对比6种常见壁面碰撞恢复方程,最终发现,在冲蚀模拟过程中,由Forder[8]提出的恢复系数方程具有更突出的优势,后被广泛运用,其壁面碰撞方程为:
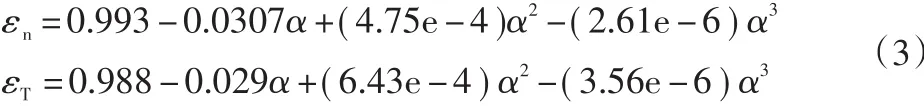
2.4 边界条件及网格划分
弯管入口边界条件采用速度入口,速度大小为4 m/s,出口采用自由出口,壁面边界条件类型设置为反弹,出口处的边界条件类型设置为逃逸,颗粒质量流量为0.212 kg/s,颗粒占液固混合物的质量分数为10%,忽略颗粒之间的相互碰撞。网格采用六面体网格划分,如图3所示。

图3 仿生弯管的有限元模型
3 计算结果
根据上述参数,将有限元模型导入Fluent仿真计算得到6种不同仿生模型和正常弯管的冲蚀速率云图,如图4所示。

由图可知,正常弯管冲蚀面积很大,主要发生在内壁外侧,仿生弯管冲蚀位置主要集中在肋条,且最大冲蚀位置均在最后一条肋条处;通过对比7种云图可知,正常弯管冲蚀情况最为严重,而仿生弯管随着偏心距离的增大,肋条冲蚀区域不断减小。
根据仿真计算结果提取出各种弯管的最大冲蚀速率,如图5所示。随着偏心距离的增大,冲蚀速率不断增大,其中偏心距离为0 mm的仿生弯管的最大冲蚀速率最小。

图5 不同类型弯管的冲蚀速率
4 结束语
通过改变仿生弯管的仿生肋条距内壁面的偏心距离,建立7种仿真模型,对比7种仿真结果可以清楚地看出正常弯管冲蚀位置主要发生在弯管内壁外侧,仿生弯管的冲蚀位置主要发生在仿生肋条上,而且正常弯管比仿生弯管冲蚀磨损要严重很多。
通过分析不同仿生弯管的仿真计算结果,可以发现:随着仿生肋条的偏心距离的增大,冲蚀速率不断增大,但冲蚀面积却不断减小,其冲蚀速率最小值为1.68×10-5kg/(m2·s),最大值为4.71×10-5kg/(m2·s),正常弯管的冲蚀速率为4.82×10-5kg/(m2·s)。

