基于多节点模型的液态熔盐堆堆芯功率控制

姜庆丰，曾文杰，谢金森，朱伟聪

(南华大学 核科学技术学院，湖南 衡阳 421001)

堆芯功率控制系统的设计技术是核反应堆控制、运行的重要课题。多节点堆芯建模方法是在反应堆点堆建模方法的基础上形成的。利用该方法所建立的多节点模型可用于堆芯功率控制系统的设计研究。多节点堆芯建模方法已受到研究者们的广泛关注，并被积极用于堆芯功率控制系统设计研究。例如，为研究模块式球床高温气冷堆堆芯控制系统特性，Dong等人[1]建立了十节点堆芯数学模型。为搭建AP1000机械补偿控制的Matlab/Simulink仿真平台，Wang等人[2]建立了堆芯多节点模型。为利用LQG/LTR(Linear Quadratic Gaussian with Loop Transfer Recovery)控制设计堆芯功率控制系统，Li[3]建立了堆芯双节点模型。

液态熔盐堆中，主泵驱动燃料熔盐在主回路系统中流动，采用控制棒控制堆芯功率。杜尚勉等人[4]基于堆芯线性化模型，采用LQG/LTR设计液态熔盐堆堆芯功率控制系统。本文基于熔盐实验堆MSRE(Molten salt reactor experiment)的实验测量数据[5,6]，采用多节点堆芯建模方法，建立MSRE的九节点堆芯模型。在此模型基础上，为实现MSRE堆芯功率控制，以PID(Proportional-Integral-Derivative)控制技术设计堆芯功率控制系统，开展堆芯反应性扰动等工况下的控制仿真，并将多节点模型下的仿真结果与点堆模型下的结果进行比较和分析。

1 堆芯多节点模型

熔盐实验堆堆芯活化区由正方形结构的石墨组件构成，两个石墨块之间的凹槽形成了熔盐燃料流动通道[7]。将熔盐实验堆MSRE堆芯划分为9个节点区域，如图1所示[6]。采用微分方程组描述所有区域内相应的状态变量，考虑到堆芯燃料的流动特性，引入时间延迟项，建立堆芯多节点模型。在建立堆芯多节点模型前，先做如下假设：

(1)在短时间内可以不考虑堆芯内碘氙等毒物的产生，因此，忽略碘氙等毒物效应。同时，假设燃料流动为不可压缩流动，不考虑燃料盐中的循环空隙率产生的反应性效应。将单个节点区域内的换热过程描述为单个节点区域内两个燃料节块与一个石墨节块的换热过程，如图2所示。最终堆芯系统被划分为18个燃料节块和9个石墨节块；

(2)考虑到熔盐实验堆中石墨中产生的热量较少，且石墨中径向和轴向的分布较为均匀，因此，不考虑堆芯石墨中径向和轴向的传热。假设堆芯节点区域中，每个燃料节块内燃料混合良好，流出燃料节块的液相温度与节块内液相温度相同；

(3)在堆芯多节点划分中，将堆芯燃料熔盐入口流量径向划分为4个不同的质量流量流入堆芯，使得燃料熔盐在堆芯中的平均停留时间与堆芯单节点模型相同。

1.1 堆芯物理模型

考虑燃料熔盐在堆芯中的流动效应，建立堆芯物理模型[5,6]。

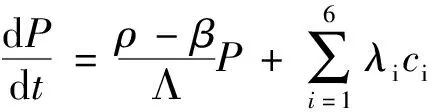
(1)

(2)

公式(2)中[5]，

(3)

(4)

公式(4)中，

公式(1)～公式(4)中：

P——反应堆功率；

ci——第i组缓发中子先驱核密度；

t——时间；

ρ——引入堆芯的总反应性；

β——有效缓发中子总份额；

βi——第i组缓发中子份额；

λi——第i组缓发中子先驱核衰减常数；

Λ——堆内中子代时间；

τc、τl——熔盐燃料在堆内的流动时间和堆外的流动时间。

对公式(1)、公式(4)两式进行归一化处理，

(5)

(6)

公式(5)、公式(6)中：

Pr(t)=P(t)/P0——堆芯相对功率；

cir(t)=ci(t)/ci0——第i组缓发中子先驱核相对密度；

P0、c0——堆芯初始稳态功率、堆芯初始稳态先驱核浓度。

1.2 堆芯传热模型

针对堆芯某一节点区域，依据图2所示划分节块。基于堆芯燃料熔盐和石墨的能量守恒，建立堆芯单个节点内的传热模型。假设燃料节块内燃料混合良好，流出燃料节块的液相温度与节块内液相温度相同，考虑单个节点区域功率值占堆芯总功率权重，通过建立每个节点中的传热模型并进行联立，建立堆芯多节点传热模型[5，6]。

(7)

(8)

(9)

式中:下标j——堆芯节点号:

Tjf1、Tjf2、Tjin——堆芯节点j中燃料节块1、节块2的平均温度及节点的燃料入口温度；

Tjg——堆芯节点j中石墨平均温度；

τjf1、τjf2——堆芯节点j中，熔盐燃料流过燃料节块1、节块2的流动时间；

mf1、mf2——堆芯单个节点中燃料节块1、节块2的质量；

mg——堆芯单个节点中的石墨质量；

K1、K2——单个节点中燃料节块1、节块2产生的堆芯功率份额；

Kg1、Kg2——堆芯单个节点中石墨节块传递给燃料节块1、燃料节块2的功率份额；

Cpf——燃料的定压比热容；

Cpg——石墨的定压比热容；

U——燃料和冷却剂间的换热系数。

堆芯燃料的平均温度Tjf为：

1.3 堆芯反应性模型

液态熔盐堆中，堆芯的总反应性可以表示为[5,6]:

ρ(t)=ρ0+ρfb(t)+ρrod(t)

(10)

公式(10)中，

(11)

堆芯温度反应性反馈主要来源于每个节点内的燃料温度反馈和石墨温度反馈。考虑到每个燃料节块或石墨节块对堆芯系统的温度反馈的贡献不同，引入权重值I。堆芯总的温度反馈反应性计算式如下:

(12)

式中:ρ0——堆芯稳态初始反应性；

ρfb——堆芯9个节点的温度反馈反应性；

ρrod——控制棒引入的反应性；

αf、αg——燃料熔盐温度反馈系数和石墨温度反馈系数；

Tjf,0、Tjg,0——表示稳态初始时刻燃料熔盐平均温度和石墨平均温度。

2 堆芯功率控制器设计

2.1 堆芯传递函数模型

选取控制棒反应性作为输入量，以堆芯相对功率作为输出量，定义堆芯模型的状态变量、输入变量和输出变量分别为：

xr=[δPr,δc1r,δc2r,δc3r,δc4r,δc5r,δc6r,δT1f1,δT1f2,δT1g,δT2f1,δT2f2,δT2g,δT3f1,δT3f2,δT3g,……,δT8f1,δT8f2,δT8g,δT9f1,δT9f2,δT9g]

ur=[δρrod]

yr=[δPr]

在某一稳态工作点，对堆芯多节点模型线性化后可得堆芯线性状态空间模型，并将其转换为单输入单输出的堆芯传递函数模型：

[δPr]=Gr(s)[δρrod]

2.2 堆芯功率控制器设计

在设计堆芯功率控制器之前，先做如下简化处理：(1)棒位变化量和其引入的反应性之间的关系用线性函数Kr表示，即控制棒每步引入的反应性为常量；(2)棒速程序单元是一个非线性单元，为了简化控制器的设计，暂不考虑死区、磁滞回环及最小和最大棒速值，仅将其作为一个增益为Kc的线性环节。设计的棒控系统如图3所示。

图3 基于核功率反馈控制的棒控系统

基于堆芯线性化模型，以MSRE堆芯为例，采用Matlab[8]软件编制程序进行堆芯功率PID控制计算。

3 堆芯功率控制仿真

3.1 研究对象

为了验证Th—U循环，熔盐实验堆MSRE利用233U做燃料开展了试验。本文以233U燃料堆芯为对象，其堆芯的主要设计参数如表1所示[4,5]。堆芯中包含4根控制棒，控制棒采用中空圆柱体，用于堆芯功率控制。MSRE堆芯9节点区域参数见表2所示[5]。233U的中子物理学参数如表3所示。

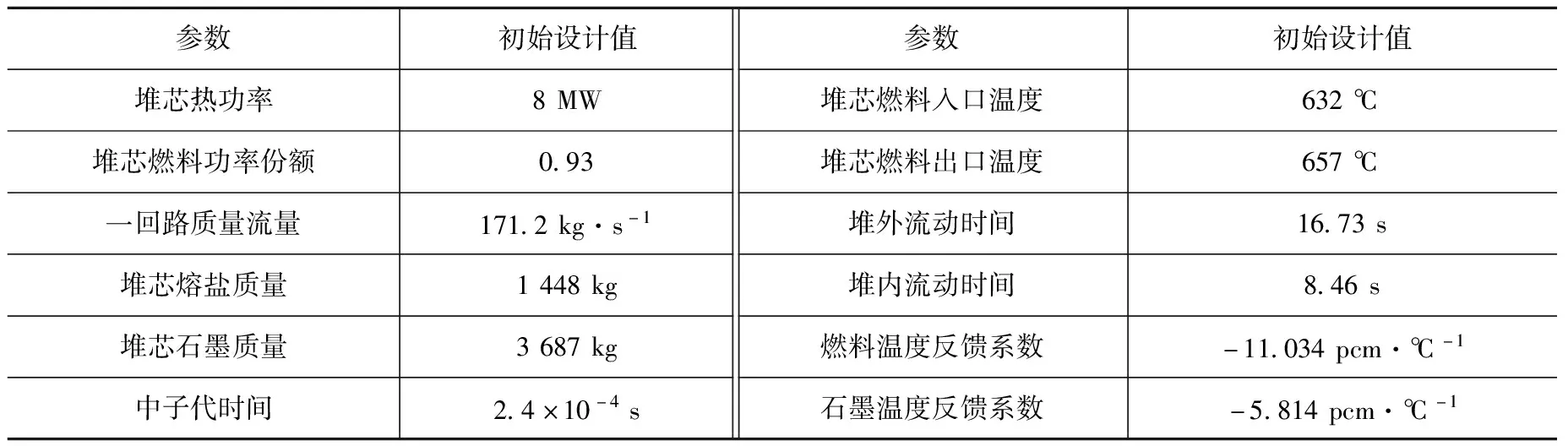
表1 MSRE堆芯的主要设计参数[4,5]

表2 MSRE堆芯9节点区域参数[5]

表3 233U燃料堆芯中子物理学参数[5]

3.2 堆芯功率控制仿真

对于装载233U燃料的MSRE系统在1 MW、5 MW、8 MW三种功率水平下阶跃引入10 pcm的反应性，仿真结果如图4所示。由图可知，在不加控制器的情况下，当系统引入反应性扰动时，系统功率超调量较大，调节时间较长。系统功率在经历上冲后，依靠燃料和石墨温度负反馈，相对功率(实际功率与相应堆芯功率的比值)偏差逐渐稳定在一个新的输出值上。在增加PID控制器的情况下，系统响应的上冲幅度减小，过渡时间较短。系统经历短暂上冲后最后稳定在一个比无控制器下的幅度小得多新的输出值。

图4 引入10 pcm反应性，堆芯功率PID控制响应曲线

在1 MW、5 MW、8 MW功率水平下阶跃引入50 pcm反应性，仿真结果如图5所示。图中可以看出，在反应性阶跃引入后功率立即有瞬间跃升，最后都稳定在一个稳定值，变化趋势同阶跃引入10 pcm反应性大致相似。由此可见，对于液态熔盐堆堆芯系统，基于堆芯多节点模型设计的PID功率控制器可以实现对反应性扰动的良好控制。

图5 引入50 pcm反应性，堆芯功率PID控制响应曲线

在1 MW、5 MW、8 MW功率水平下，模拟堆芯系统在初始100 s内按初始稳态功率运行，在100 s时堆芯功率水平阶跃至稳态初始功率的90%，然后稳定运行550 s后，在650 s时刻，堆芯功率水平阶跃至稳态初始功率水平，点堆模型与多节点模型在PID控制器下的仿真结果如图6所示。图中可以看出，在PID控制器下，基于点堆模型、多节点模型计算得到的相对功率变化均与参考功率变化要求保持一致。可见，采用PID进行点堆模型和多节点模型下的堆芯功率阶跃控制是可行的，且多节点模型比点堆模型控制效果更好。

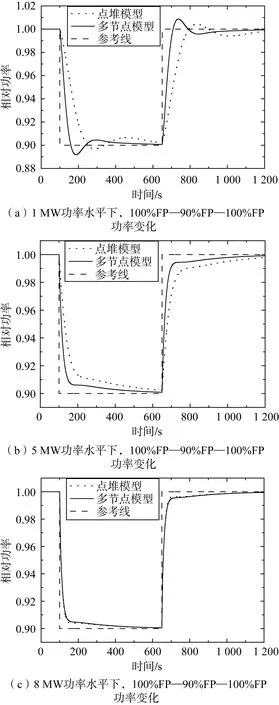
图6 装载233U燃料的堆芯功率PID控制响应曲线

4 结论

本文针对液态熔盐堆堆芯功率控制问题，基于堆芯多节点模型和PID控制技术建立了堆芯功率控制系统。通过对比阶跃反应性扰动下有、无控制器的仿真结果，证实基于堆芯多节点模型设计的堆芯功率控制系统可以实现堆芯功率调节与稳定。在堆芯负荷变化情况下，与基于堆芯点堆模型设计的功率控制器相比，基于堆芯多节点模型设计的功率控制器响应速度更快、超调量更小，实现堆芯功率稳定能力与功率调节能力更强。