点堆随机动力学微分方程的推导

刘建军,朱家彩，王瑞利，傅学东，任 键

(北京应用物理与计算数学研究所,北京100088)

核反应堆点堆动力学方程是一个描述与时间相关的中子数密度和缓发中子先驱核浓度的常微分方程组。点堆动力学常微分方程组存在单能中子假定、无空间效应等物理描述的局限性。并且该方程组对所有的微观过程(从核裂变放出中子、介质中的中子输运、次级核裂变)的每一个环节都是离散的随机过程，最终都要求进行统计处理。

这种处理，只是把本来是随机过程的中子密度时空分布作为连续函数的输运理论、或扩散近似的一种近似描写[1]。这种处理通常描述的是系统内中子数密度、缓发中子先驱核浓度、功率状态的平均值或期望值。所以，点堆模型核反应动力学方程实际上是确定论的常微分方程，其解也是确定论的平均或期望值。

然而，实际的反应堆动力学过程往往是随机的，自然，中子密度和缓发中子先驱核浓度随着时间变化往往是随机涨落的。在高功率状态，其随机行为是可以忽略的。但是，在近临界、低功率状态，例如，在弱源条件下的反应堆启动、临界安全分析、快中子脉冲堆爆发脉冲实验时[2,3]，初始阶段将会出现中子密度和缓发中子增殖过程中的随机性涨落、以及辐射剂量的不确定度问题，这就特别需要我们从理论和技术上进行把握和掌控，以求准确地评估其范围和风险。

显然，我们常用的传统反应堆动力学方程组并不具备处理上述物理现象的功能。这是因为，如果在系统中仅有少量的中子、或有随机因素时，则在系统内、各空间点上单位体积元内中子数的多少也许不是平均值，而是一个随机事件，系统中的中子数可能会非常迅速的增殖，也可能会全部死绝。

虽然，MC方法具有处理此类随机事件的独特优势，也最常见。但是，MC方法运算速度慢、人力物力成本相对较高是其主要缺点。

俄罗斯学者在这一问题研究中独具特色，尤其在反应堆无外源启动的理论研究和应用实践中成果显著，Ю.В.沃尔科夫1988年就提出来随机动力学的概念。

1992年在他的《弱源条件下的反应堆随机动力学与核安全研究》[4]一文中简单介绍了可将随机微积分应用于描述反应堆物理中的随机现象，并给出了一组点堆随机动力学微分方程组。他指出，可以用这一方程组来描述反应堆弱源启动过程中中子的随机性涨落物理现象、堆内多群中子持续时间内的随机轨迹过程、讨论中子数的随机行为和源强对核安全影响的重要性。

虽然他没有介绍推导过程，也没有介绍求解计算方法，我们也难以直观简单地判断其方程的正确性，但是作者创新地在点堆动力学方程中引入了随机项的建模思路引起了我们极大的关注和兴趣。

随机微积分方法是近年来国际多学科领域处理各种随机现象的一种热门的数学方法，日本数学家K.Ito(伊藤清)在这一数学领域的成果引起了国际学术界的极大关注与赞赏。即，求解随机微分方程最有实用意义的近似方法是伊藤清提出的Ito公式，有了Ito 公式之后，就可以计算一些基本常用的随机微积分方程。

事实上，这一建模及数学处理方法已经普遍在国际金融、特别是股票交易中涨落情况的预计分析、水利、工程可靠性及不确定性分析等具有随机事件的领域中都看到诸多成功的研究和应用范例[5-7]。但尚未见到有国内学者在反应堆物理中的应用实践。

我们借鉴俄罗斯学者Ю.В.沃尔科夫的思想，仔细推导了点堆随机动力学微分方程组、在点堆动力学方程中引入随机项的理论研究工作。其目的是，探索快速计算和准确评估反应堆弱源启动过程中的中子增殖随机性涨落物理现象及不确定度，并希望引起国内学者的兴趣与关注。

本文第一节，介绍了我们拟研究的物理问题，简介了Ю.В.沃尔科夫的方程组。第二节介绍了我们从中子随机事件的基本假定出发，推导点堆随机动力学微分方程组的过程和结果，并指出了Ю.В.沃尔科夫方程组的错误。

1 物理问题与沃尔科夫方程组

一般情况下，对于强中子源的核反应堆启动、运行、或失控时，应用我们熟知的点堆核反应动力学常微分方程组来描述中子的增殖过程是可信的，也不存在随机问题，只需正确地描述并且考虑最初的无限裂变链出现的概率即可。

然而，常用的点堆反应动力学方程在处理和描述含有弱中子源的反应堆启动、临界安全分析、脉冲堆爆发脉冲实验等物理过程时，就容易出现中子增殖过程中因各种随机事件发生随机性涨落。例如田湾核电站无源(实为燃料棒的自发裂变源)启动的反应性测量曲线则直观地展现了弱源启动阶段反应性与中子增殖过程中的随机涨落现象[8-10]，如图1所示。

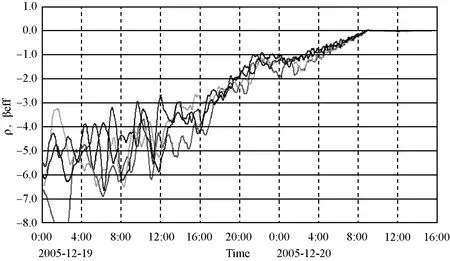
图1 田湾核电厂无源启动反应性测量曲线

此时，对于这种增殖过程存在随机性涨落，如果采用统计平均的处理方法是存在问题的。

再如，1960年美国学者T.F.Wimett等人公开发表了在Godiva-Ⅱ脉冲堆进行的弱源爆发脉冲实验[3]，也揭示了快堆启动中的随机行为和复杂的物理现象。其主要特征是每次爆发脉冲堆时间呈随机性，总的爆发脉冲等待时间概率分布具有规律性，还会出现提前爆发脉冲现象，(在脉冲棒未达到预定反应性时就已经提前爆发脉冲)。

中国工程物理研究院物理与化学研究所也重现了这一现象[11]。

所以，在弱源条件下的核反应堆启动与安全运行控制时，就要特别关注反应性、或中子数和缓发中子先驱核的随机涨落及不确定度，因为，在弱源条件、当k=k(t)时，这种随机涨落现象及不确定度将影响反应堆的启动时间，也关系到反应堆的安全风险分析的准确性。

传统的点堆模型动力学方程实际上是一个数量相互作用的模型系统，特别是中子的数量和缓发中子先驱核的数量，当物理的动力学系统被标示为数量过程后，在技术上可以把确定论的点堆动力学方程发展为随机微分方程系统，即，成为实际的随机行为过程模型，该随机微分方程也概括了确定论的点堆动力学方程。

如序言所述，俄罗斯学者Ю.В.沃尔科夫提出了随机动力学的概念，介绍了可用随机动力学微积分方程组来描述反应堆物理中的随机现象。沃尔科夫方程组形式如下：

(a)

(b)

i=2,m+1；

(c)

(d)

n=2,m+1；

(e)

(f)

n=2,m+1；

但是，由于沃尔科夫既没有介绍推导过程，所以，需要我们通过推导和求证去判断公式是否正确。

2 点堆随机动力学微分方程理论推导

本节我们将推导和建立引入了随机项的点堆随机动力学微分方程组。

考虑一个十分小的时间间隔Δt，Δt时间内有2+Q种不同事件单独发生。因为Δt足够小，可以假定任何两种事件不同时发生，y1(t)表示系统内中子数随时间的变化，考虑存在两组缓发中子β2、β3，则Δt内有6种不同事件单独发生，

第一种可能的贡献，俘获：

(1)

Δt内俘获中子的事件的概率为:

(2)

第二种可能的贡献，定常中子源S在Δt内发源射中子:

(3)

定常中子源S在Δt内发射的概率为:

P2=SΔt

(4)

第三种可能的贡献，Δt内裂变释放ν1个中子:

(5)

Δt内裂变释放ν1个中子的概率为：

P3=ΣfυΔty1P(ν1)

(6)

第四种可能的贡献，Δt内裂变释放ν2个中子:

(7)

Δt内裂变释放ν2个中子的概率：

P4=ΣfυΔty1P(ν2)

(8)

第五种可能的贡献，Δt内先驱核y2衰变：

(9)

Δt内先驱核y2衰变的概率为：

P5=λ2y2Δt

(10)

第六种可能的贡献，Δt内先驱核y3衰变：

(11)

Δt内先驱核y3衰变的概率为：

P6=λ3y3Δt

(12)

上述式中，y1(t)表示系统内中子数随时间的变化；先驱核的份额分别为β2、β3；裂变产生次级中子的数目ν1和ν2的分布为P(ν1)和P(ν2)。y2、y3分别为缓发中子先驱核的数目；L是中子寿命；Pi为产生事件i的概率；υ为中子速度；Σa为中子的宏观吸收截面；Σf为中子的宏观裂变截面；Σγ为中子的宏观俘获截面。

则有Δy1、Δy2、Δy3的数学期望值为

(13)

则有：

(14)

平均协方差

(15)

λ2y2Δt+λ3y3Δt+ΣfvΔty1P(ν2)[-1+(1-β)ν2]2

λ2y2Δt+λ3y3Δt

(16)

B12Δt=P1[Δy1Δy2]1+P2[Δy1Δy2]2+…+P6[Δy1Δy2]6

=0+0+ΣfvΔty1P(ν1)[-1+(1-β)ν1]β2ν1

+ΣfvΔty1P(ν2)[-1+(1-β)ν2]β3ν2-λ2y2Δt

(17)

(18)

(19)

比较可知，

B21=B12

(20)

B31=B13

(21)

(22)

(23)

B23Δt=P1[Δy2Δy3]1+P2[Δy2Δy3]2+…+P6[Δy2Δy3]6

(24)

同样有：

B32=B23

(25)

以此类推，我们就不难得到与沃尔科夫方程相似的方程组及其元素Bij，表达式如下：

(26)

式中，y(t)=[y1(t),y2(t),…ym+1(t)]是矢量；y1是反应堆内中子数；

[y2(t),…ym+1(t)]是相应的缓发中子组队先驱核数目；

矢量ξ(t)=[ξ1(t),ξ2(t),…ξm+1(t)]由多个标准的高斯白噪声组成；

式(26)中右侧部分白噪声的存在表示中子出生和死亡等基本过程的特征，其特征时间≪L。

gij是解矩阵方程GGT=B的元素，维数为(m+1)(m+1)的矩阵，Bij的元素为：

(27)

(28)

(29)

(30)

到此，我们得到了完整的随机中子微分方程组式(26)～方程组式(30)。

该方程组被称为随机点堆动力学微分方程，其调节部分与点堆动力学方程完全相同。不同的是，式中引入了随机项∑gij(y)ξi(t)，或称为伊藤随机项。如果矩阵方程GGT=B=0，则方程组可退化为标准的点堆动力学方程。

方程组可以描述反应堆内有少量的源中子和存在多群缓发中子先驱核的连续时间内的随机过程的轨迹。为了评估反应堆的安全性，或发生事故时的辐射剂量，则必须弄清y(t)=[y1(t),y2(t),…ym+1(t)]的时间过程，

还必须解决中间概率下的多为扩散过程y(t)的边界问题，该问题都可通过上述点堆随机动力学微分方程组来描述。在引进了随机项后，就可以来描述中子增殖过程中的随机涨落现象，而不仅仅是期望值。

我们把本文得到的方程组与沃尔科夫的方程组和元素Bij进行了仔细的对比。我们发现不知是沃尔科夫笔误还是印刷错误，在他的方程组与脚标存在以下多处错误：

(c)式中有bii、yi、i=1三处脚标错误，正确应分别为b11、y1、i=2。

通过上述工作，我们发现了沃尔科夫点堆随机动力学方程组的某些错误，得到了正确的方程组，这将为我们后续对方程组的求解方法研究和实验的模拟奠定了可靠的基础。我们研究认为，虽然沃尔科夫所给的方程组存在一些笔误或错误，但他的物理思想是科学创新的。而且，随机反应堆动力学方程也将是今后反应堆物理中值得研究和发展的方向之一。

本文介绍这一物理问题和方程组的推导过程，目的也是想引起业内同行的兴趣和关注，今后，我们将陆续给出这一方程组的求解方法研究和实验模拟的结果。

3 结论

针对反应堆物理中的随机问题的研究，通过调研和借鉴国外学者的理念，我们尝试着将随机微积分理论引入于反应堆物理，在点堆模型假定下，仔细推导了可描述随机现象的点堆随机动力学微分方程组，发现并纠正了沃尔科夫方程组的错误。这将为我们进行方程组的求解方法研究和实验的模拟奠定了可靠的基础。