乏燃料公路运输事故条件下放射性核素弥散模型研究

陈黎伟，陶龙龙，周百昌，汪 进，龙鹏程，王 芳

(1.中国科学院核能安全技术研究所 中子输运理论与辐射安全重点实验室，安徽 合肥230031；2.中国科学技术大学，安徽 合肥 230027；3.安徽省核应急专业技术支持中心，安徽 合肥 230031；4.中国人民解放军96901部队23分队，北京 100095)

截至2018年9月，我国有44个核反应堆在运行，容量为40.6 kMW，13个在建，容量为14 kMW，并计划增建36 kMW瓦的核反应堆，到2020年，中国将拥有58 kMW的容量，乏燃料累积量将达到近9 000 tHM[1, 2]。2017年，我国出台的《核安全与放射性污染防治“十三五”规划及2025远景目标》文件强调要推进乏燃料贮存和处理能力建设，建立保障机制，优化运行管理。可见，乏燃料管理已成为我国核燃料循环技术发展的重点问题[2, 3]。

乏燃料管理有三种主要方式：直接处理、后处理和乏燃料出口。无论是哪种方式，乏燃料运输在乏燃料的管理中都起着关键作用[4]。然而，乏燃料在运输过程中可能会受到不可抗力因素的影响，如：灾害天气、车祸、人为误操作等，导致乏燃料组件及运输容器受损，从而发生放射性核素泄漏[5]。泄漏的放射性核素会从燃料组件到运输容器内腔再释放到外部环境，对环境造成放射性污染[6]。有统计显示，美国在1974年至1993年间与放射性运输容器表面污染相关事故共53起[7]；2013年，欧盟一辆装载乏燃料容器的火车因脱轨而导致有放射性污染源泄漏，且有25万人居住在距离事故发生地仅2.5公里的范围内[7]；我国在1988年至1998年有13起与放射性材料运输相关的事故，且造成了57人受照[8]。李越等人系统分析了国内外乏燃料运输现状及存在的问题，指出目前我国主要的运输方式为公路运输，并提出现阶段应加强乏燃料运输事故情景及后果评价方面研究[2]。相对于乏燃料存贮泄漏事故[9]，由于事故地点的不确定性，乏燃料运输事故具有更大的辐射风险[10]，因此，事故条件下乏燃料公路运输核素弥散后果评价技术对于当前我国核事故早期应急是必不可少的。

乏燃料运输事故后果评价关键技术中，大气弥散模型是计算个人剂量与集体剂量的基础，美国基于高斯模型开发的RADTRAN软件实现了放射性材料运输辐射影响的计算和评价[11]；我国王任泽等人基于高斯模型开发了放射性物质运输后果评价软件CRAMTRA1.0，并进行了对比测试[10]，马文娟等人利用CRAMTRA1.0软件分析了在三种运输方案下乏燃料从中国广东某核电站到西北地区后处理厂的辐射影响[12]。然而，运输事故过程中的放射性物质扩散与迁移具有室外复杂环境的特点，如沉降、植被效应、复杂地形与建筑等，尤其当泄漏源高度位于植被或建筑物高度以下时，其泄漏的核素受植被效应与建筑物壁面效应影响较大，而高斯模型对于此类情况下并不能很好的模拟[13]。

计算流体力学(CFD)方法是解决复杂条件下大气污染物弥散分布的有效工具[14]。谢清芳等人利用CFD方法，分析了不同来流方向条件下植被对铀尾矿库下风向氡的扩散分布及规律的影响[15]。Ghasemian等人利用CFD方法模拟了植被屏障下的流场和交通排放污染物浓度，为城市规划者提供了一些有效建议[16]。Wang CH等人基于CFD方法系统分析了树木与道路两边建筑物高度差异及道路两边建筑间隔距离差异对交通排放大气污染物扩散规律影响机制[17]。相比于交通污染源近地面排放，乏燃料公路运输泄漏事故还具有泄漏源位置不确定性的特点，从而为放射性污染物扩散与迁移带来了不确定性。

凤麟核能团队围绕反应堆事故诊断、放射性核素环境影响、核应急与公共安全等迫切需求，依托中子输运设计与安全评价软件系统SuperMC[18]、可靠性与概率安全分析软件系统RiskA[19]、核安全云NCloud等核心基础，建成了数字社会环境下的虚拟核电站Virtual4DS[20]。本文通过修正放射性核素衰变项及动量源损失项，提出一种基于CFD方法的乏燃料运输事故条件下的放射性核素弥散模型，并在Virtual4DS框架下，基于OpenFOAM 4.1软件引擎进行求解器开发以实现事故场景模型的数值模拟，且在模拟中结合不同泄漏源高度及有无树木影响的条件，实现了乏燃料公路运输事故下放射性核素分布，同时对比分析了不同条件下的核素弥散分布规律。

1 模型描述

1.1 乏燃料运输事故场景描述

根据2003年国家核安全局发布的《关于颁发大亚湾核电站乏燃料公路运输装运批准书的通知》文件内容[21]，从大亚湾核电站运往甘肃四○四厂乏燃料后处理厂，途经广州、长沙、武汉、信阳、漯河、郑州、洛阳、西安、咸阳时为高速路段，从咸阳、兰州、武威、甘肃乏燃料后处理厂时为国道路段。图1为谷歌卫星地图中的信阳至漯河高速路段的乏燃料运输路线场景图，图1(a)表示有树条件下的运输场景；图1(b)表示无树条件下运输场景。此类场景中道路两旁均有建筑民房、服务区，为居民密集区，一旦发生核泄漏事故，将对周边环境和人身造成放射性危害。因此，本文基于类似场景作为研究样地进行场景建模。

图1 乏燃料公路运输路线场景

假设一辆乏燃料运输卡车从临时储存库行驶到后处理厂，车上装有用于储存压水堆(PWR)燃料组件的NAC-STC型乏燃料容器。由于运输乏燃料金属容器中使用的金属垫圈受到长期的高温影响，金属垫片的残余线性载荷和总回弹距离因软金属外层护套的蠕变变形而松弛，在受到撞击或其他机械振动后，乏燃料容器密封条发生松动。因此，放射性核素从储罐泄漏到环境中[22]，以气载的形式在环境中扩散和迁移，并在植被和土壤上沉积，对周边环境造成了辐射危害[23]。

当树木高于建筑物时，其对峡谷气流和污染物浓度影响最大[17]，本工作主要考虑树木高于建筑物的情况。乏燃料运输场景的几何模型如图2所示，假定计算域为64H(x方向)×70H(y方向)×8H(z方向)(其中H=18 m)，建筑物、树木和道路位于计算域的中部，其长度为10H(180 m)。道路的宽度是2H(36 m)，从建筑物到车辆行驶道路的距离是2/3H(12 m)，树木位于建筑物和车辆行驶道路之间，宽度是1/3H(6 m)，高度是3/2H(18 m)，从建筑物到树木的距离是1/3H(6 m)。大气气流沿x正向垂直于道路方向经过。

为准确评估放射性核素对两边建筑的辐射危害，假设靠近来流处的建筑物且离释放源最近的壁面为壁面一；靠近去流方向处的建筑物且离释放源最近的壁面为壁面二。

图2 乏燃料公路运输事故几何模型

1.2 数学模型

近地面气流在地面、植被、建筑等复杂条件的影响下，较易形成湍流[24]。为准确预测乏燃料公路运输事故中泄漏核素的分布状态，本文引入标准k-ε湍流模型，综合考虑核素衰变及动量源的损失，建立了基于CFD方法的修正模型，用于模拟事故条件下的放射性核素弥散过程。模型中主要包括两个部分，即流场模拟和放射性核素浓度模拟。

1.2.1 流场模拟

本文假设计算区域内空气流动为不可压缩流动，且考虑重力损失，由于在处理植被影响下的大气污染物扩散时，可将树木区域视为多孔介质[16, 25]，以压力损失系数近似气流在通过植被时产生的压力损失，可以通过增加动量源损失项来修正动量守恒方程，以模拟树木作用下的流场分布。简化后的质量守恒方程与动量守恒方程如下：

质量守恒方程：

(1)

式中：ui(m·s-1)为速度分量，i=1,2,3分别对应x,y,z三个方向。

动量守恒方程：

(2)

式中：t——时间，s；

ρ——流体的密度；

P——压力，N·m-2；

μ,μi——分别为动力粘度和湍流粘度；

g——重力加速度，m·s-2；

Sui——动量源损失项;

λ——压力损失系数,m-1。

1.2.2 放射性核素浓度模拟

在大气环境中，放射性核素浓度方程可表示为：

(3)

式中：C——坐标点(x，y，z)处的每个时间步的浓度值，kBq·m-3;

ΓC(m2·s-1)——湍流扩散系数,m2/s;

SC——源项kBq·m-3·s-1。

在乏燃料公路运输事故场景中，泄漏的放射性核素会因大气流场的驱动，受树冠效应、壁面效应、放射性衰变和沉积[26,27]的影响，逐渐向周围环境扩散和迁移。因此，我们需要对浓度方程作沉积、核素衰变等修正，然而，碘在乏燃料公路运输事故中主要以气相形式迁移，且只有极小的粒子(平均粒径在2 μm以内)从容器中释放出来[28]。因此，对于事故早期应急(0.5 h～1 d)，放射性核素沉积量可以忽略不计。

其浓度修正方程可以表示为：

(4)

式中：λd——核素衰变因子;

T1/2——核素半衰期。

1.3 模型验证

由于辐射危害，用实验方法较难验证乏燃料公路运输过程中的核素弥散过程。本工作将采用Jeanjean APR等人工作[25]中模拟的数据作为验证案例，该验证模型由一个街道峡谷组成，树木宽度与高度比例为1∶1，在树木两边分别有一排10H(长)×H(宽)×H(高)的建筑物(H=18 m)，气流从垂直于建筑物x轴正方向经过，在两排建筑中间和模型树的底部有四条线源发射器，用于释放出气体示踪剂SF6，其释放率为Qi。其他边界条件及参数设置参见文献[25]，最后将浓度值使用归一化浓度公式进行表示：

(5)

图3为Jeanjean APR等人在靠来流方向较近的建筑壁面的浓度模拟结果与本工作模拟结果的比较，其中图3(a)表示为有树条件下的空街峡谷墙壁归一化浓度模拟，图3(b)表示为无树条件下的空街峡谷墙壁归一化浓度模拟。从模拟的结果可以看出，连续释放源在风场及建筑壁面的作用下，在建筑壁面中间产生蓄积，且由于树木的作用，造成了示踪气体浓度的升高，可见两项工作在模拟的浓度分布情况是一致的。虽然部分区域等值线存在一些较小差异，这主要是因为本文在网格处理上与Jeanjean APR等人可能有所不同，但总体浓度扩散趋势与分布是一致的。

图3 靠来流方向较近的建筑壁面的浓度模拟

2 数值模拟

2.1 计算方法

在OpenFOAM 4.1多孔介质求解器的基础上添加了修正后的浓度方程，对求解器进行重新开发，以适合本工作的需求。

具体开发步骤如下：

(1)创建输入变量场：在多孔介质求解器中创建三个标量场(浓度场C、压力场p，湍流扩散系数alphat)和一个矢量场(速度场U)；

(2)添加浓度方程头文件CEqn.H：头文件中写入本文中的浓度输运方程；

(3)添加传输参数头文件：readTransportProperties.H：添加求解过程中所需要的参数，如：层流Prandtl数，湍流Prandtl数，衰变因子，沉积因子等；

(4)与速度、压力联立求解。在执行文件中(.C文件)添加 #include “CEqn.H”，使其基于pimple算法进行压力速度耦合求解；

(5)最后进行求解器编译；

(6)在算例求解过程中，给定速度、压力、湍流扩散参数，湍动能、湍流耗散率、源项等初始条件和边界条件，利用topoSet命令对树木多孔介质区域进行指定，先对大气风场进行稳态求解，最后将求解后的稳态风场作为初始条件，使用自定义求解器进行迭代求解。

另外，输运方程均采用有限体积法离散[14]，所有方程采用中心差分格式和迎风格式进行求解。

2.2 边界条件

在乏燃料运输中，假设天气晴朗，环境温度为20 ℃，且为等温状态。空气密度应为1.2 kg·m-3。事故发生在场景模型正中心位置，泄漏引起了放射性核素131I的连续释放，泄漏率为3.3 kBq·m-3·s-1，大约为0.72 μg·m-3·s-1质量流量，碘在空气中的扩散系数约为0.8×10-5m2s-1[29]，来流沿x正方向的初始风速为2 m·s-1，壁面边界采用Neumann边界条件，且为固体壁面无滑移条件，流体通过树木的压力损失系数为200，湍流长度尺度(Λ)通过选择来流直径确定。根据公式(6)至公式(8)对雷诺数(Re)、初始湍流动能(k)和湍流耗散率(ε)进行初始值设定。

(6)

(7)

(8)

本工作主要计算泄漏事故后发生的1 h以内的放射性131I连续释放，分别考虑泄漏源在2 m(位于建筑物高度以下)和22.5 m(位于建筑物高度与树高度之间)的高度，以表示运输车辆经过普通路面、桥或边坡等不同路面高度的情形。由于空气中的碘摩尔分数是约为4.36×10-11，因而不影响空气混合物流动性能，为了向核应急决策者提供更多的实际信息，在结果讨论中考虑工作场所的131I最大允许浓度为0.33 kBq m-3[9]。

2.3 网格无关性测试

图4 在t=720 s时刻y=630 m平面在z=2 m高度131I从x=558 m至x=594 m区间浓度

2.4 分析与讨论

为了获取不同乏燃料公路运输场景下的核素弥散分布规律，下面结合有无树木影响及不同源高两个部分，从大气流场的分布、浓度空间分布与建筑壁面浓度时间变化等方面对乏燃料运输事故条件下放射性核素131I弥散规律进行了对比分析。

图5 y=630 m平面释放源附近稳态风场分布

图5表示y=630 m平面释放源附近稳态风场分布，其中图5(a)表示无树条件下的风场分布；图5(b)表示有树条件下的风场分布(虚线区域内表示树木)。从图中可以看出，树木对建筑物之间的湍流漩涡有明显的减弱作用，在无树条件下，建筑物之间产生了较大涡旋，相比之下，有树环境下的建筑物之间则没有大的涡旋作用。

图6给出了z=2 m高的释放源131I在y=630 m平面第3 600 s时的浓度分布情况，其中图6(a)表示无树条件下的浓度分布；图6(b)表示有树条件下的浓度分布。无树条件下的放射性核素131I受湍流回流作用向来流方向逐渐扩散，对靠近来流方向的建筑物污染较大。然而在有树条件下，因两建筑物之间涡旋效应被减弱，131I向泄漏源四周扩散较为明显，且在风场的作用下，扩散逐渐向去流方向偏移，对去流方向建筑物逐渐造成污染。可以看出，树木对放射性核素扩散范围起到了一定的抑制作用。

图6 z=2 m高的释放源131I 在y=630 m平面t=3 600ths的浓度分布

从图7中可以看出，无树条件下的壁面一的131I最大浓度和平均浓度都明显比壁面二要高。但是有树条件下的情况恰恰相反，壁面二的131I最大浓度和平均浓度都明显比壁面一要高，这是因为在无树条件下131I受到回旋涡流的影响，释放的核素不断向来流方向建筑壁面蓄积，从而导致壁面一的放射性核素浓度较高现象。通过模拟，我们可以得到第3 600 s在无树条件下，壁面二的131I平均浓度为0.005 kBq·m-3，比壁面一的平均浓度(0.025 kBq·m-3)低5倍；有树条件下，壁面二的131I平均浓度为0.008 9 kBq·m-3，比壁面一的平均浓度(0.003 2 kBq·m-3)高2.8倍。而且，在相同边界条件下，壁面一在无树木条件的131I平均浓度比有树条件下高7.8倍。由此可见，建筑物之间的树木对建筑物的放射性污染起到了一定的抑制作用，且要加强无树条件下来流方向附近的建筑物壁面去污工作。

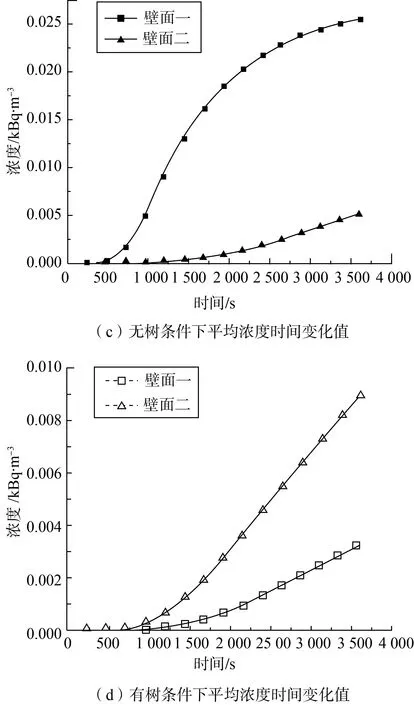
图7z=2 m高的释放源131I在建筑物壁面的浓度

Fig.7131I concentration of the walls of the building at thez=2 m leakage height

图8给出了z=22.5 m高的释放源131I在y=630 m平面第3 600 s时的浓度分布情况，其中图8(a)表示无树条件下的浓度分布；图8(b)表示有树条件下的浓度分布。在无树条件下泄漏的放射性核素首先向去流方向扩散，对去流方向较近的建筑物造成了污染，然后部分核素被涡旋捕捉后逐渐向来流方向建筑物扩散。在有树条件下，释放源逐渐在两树之间较为均匀的向四周扩散。相比源高z=2 m时131I浓度分布情况，无树条件下131I扩散趋势呈明显不同，这主要是因为建筑物之间的涡流对扩散造成的影响。

图8 z=22.5 m高的释放源131I 在y=630 m平面t=3 600th s的浓度分布

图9 z=22.5 m高的释放源131I在建筑物壁面的浓度

从图7和图9中可以看出，无论释放源在何处，有树条件下的核素浓度增长变化曲线相对平缓。与源高z=2m情况不同的是，当释放源高位于z=22.5 m时，无树条件下的壁面一的131I最大浓度和平均浓度都明显比壁面二要低。而在有树条件下的情况相对复杂，从第0 s到1 680 s，壁面二的131I最大浓度均比壁面一要高；从1 680 s后，壁面一的131I最大浓度均比壁面二要高；但是对于两旁建筑物的壁面平均131I浓度变化值非常接近，呈线性增长趋势。这是因为在无树条件下131I主要直接受到去流风的影响，释放的核素不断向去流方向扩散，对壁面二建筑壁面直接造成了放射性污染；有树条件下泄漏源周围去流方向风得到了减弱，131I不断向四周均匀扩散。通过模拟，我们可以得到第3 600 s时刻在无树条件下，壁面二平均131I浓度为0.006 6 kBq·m-3，比壁面一平均131I浓度(0.001 5 kBq·m-3)高4.4倍；比有树条件下的壁面二平均131I浓度(0.002 1 kBq·m-3)要高3倍。由此可见，当源高位于建筑物以上，树以下时，无树条件下去流方向附近建筑放射性污染较为严重。

3 结论

本文基于CFD的方法研究了乏燃料公路运输事故条件下放射性核素弥散过程，而且我们可以通过此方法得到乏燃料运输事故后不同泄漏源位置放射性核素的具体分布情况以及对周边建筑的辐射危害，从而可以为核应急工作者提供参考依据。此外，根据模拟，我们主要得出了以下结论：

(1)湍流漩涡的减弱效应对泄漏源扩散范围起到了一定的抑制作用，从而影响了核素分布规律。

(2)当源高位于建筑物以下，有树条件下，去流方向附近的建筑放射性污染较来流方向附近的建筑严重。相反，在无树条件下来流方向附近的建筑放射性污染较去流方向附近的建筑严重。

(3)源高位于建筑物以上树以下，有树条件下，泄漏源均匀向四周扩散，对道路两边建筑造成的放射性污染相当。而在无树条件下，去流方向附近的建筑物的放射性污染比来流方向附近的建筑物污染要严重。

因此，当泄漏源发生在不同高度时，泄漏源对道路两边的建筑所造成的放射性污染程度都是明显不同的。在此基础上，我们对核应急工作者提出了两点建议。对于发生乏燃料运输事故后处理，应首先判断泄漏源、树木、建筑物的相对高度，然后通过放射性核素弥散模拟的方法估计放射性危害区域，从而为核事故后的放射性处置提供更加真实的信息。

致谢

本论文得到中国科学院信息化专项项目(XXH13 506-104)，中国科学院青年创新促进会专项项目资助。同时衷心感谢凤麟团队全体成员的帮助和指导。