基于GARCH族模型的创业板市场波动性问题研究
宋永辉 许倩
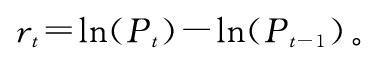

摘要:创业板的建立对我国实体经济起到了重要作用,但是创业板市场存在着较大的波动性,所以本文以创业板指数收益率为研究对象,构建GARCH族模型对其收益率序列的波动性进行研究。研究结果表明:创业板指数收益率序列的波动具有集聚性、持续性和非对称性,上述分析结果可以为创业板收益率波动的预测提供指导作用。
关键词:创业板;ARCH效应;GARCH模型;波动性
中图分类号:F831文献识别码:A文章编号:2096-3157(2020)06-0098-02
一、引言
创业板设立的主要目的是为中小高新技术企业提供融资渠道,自首批28家企业上市以来,创业板市场为大量的中小高新技术企业提供了资金支持,推动了中小企业的发展,但是与发达国家成熟的创业板市场相比,我国创业板市场仍然存在很多不足,例如“三高现象”、新股炒作、业绩变脸等问题,这使得我国创业板市场具有较大的波动性,易造成风险的积聚,阻碍创业板市场的健康运行,所以对创业板市场波动性特征进行研究具有重要的意义。
本文运用GARCH族模型对创业板指数收益率序列的波动性进行研究,从而发现其波动性规律和特征,为创业板收益率波动的预测提供指导作用,对投资者进行投资决策也具有参考价值。
二、文献综述
高金莎(2017)通过GARCH及其拓展模型对上证综合指数进行建模,发现上证综指的波动存在丛聚性、持续性和非对称性。丁扬恺(2012)运用GARCH-M模型和EGARCH模型对深证成指20年的数据进行实证研究发现,深证成指收益率的波动性具有持久性和不对称性,而且EGARCH模型比GARCH-M模型具有更好的适用性。黄灿(2014)以我国创业板指数为研究对象,对创业板指数收益率进行统计检验和ARCH效应检验,发现其收益率序列存在着条件异方差,通过建立GARCH模型和GARCH-M 进行分析,发现创业板收益率序列的波动存在丛聚性和杠杆效应。赵鹏举等(2019)利用GARCH-VAR模型比较创业板和主板的波动性特征和市场风险,得出在不同的分布下,GARCH 模型都能有效地反映股票收益率序列的尖峰厚尾的特征,且创业板市场相对于主板市场有更高的风险,同时也具有较高的回报率。
三、数据选取和描述性统计分析
1.数据选取
本文选取创业板指数2010年6月1日至2019年12月26日的日收盘价为样本区间,样本容量为2328个,数据从同花顺软件获得,收益率采用对数收益率,即:rt=ln(Pt)-ln(Pt-1)。
2.描述性统计分析
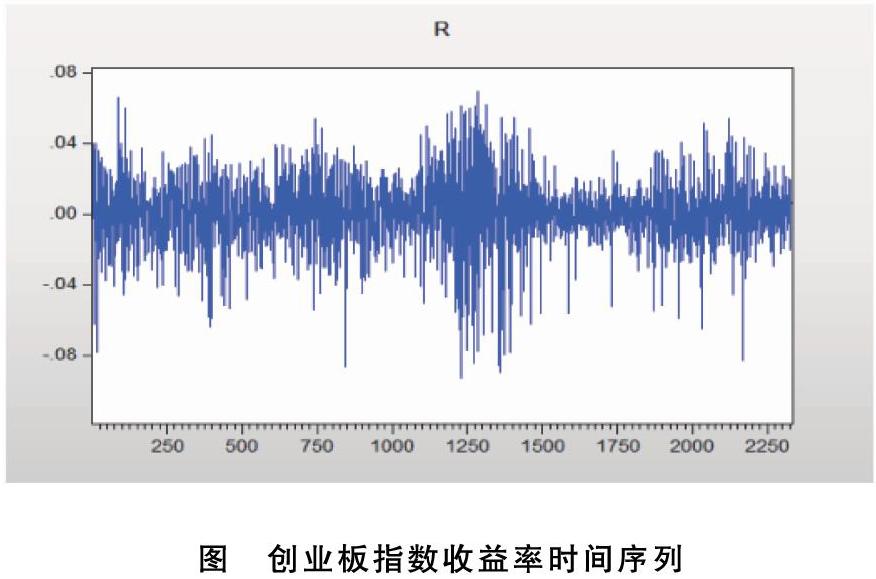
本文运用Eviews软件做出创业板指数收益率序列的线性图,结果如图1所示。
由图可知,创业板指数收益率表现出波动集聚性和波动持续性,即大的波动后面伴随着较大的波动,小的波动后面伴随着较小的波动。
进一步对创业板指数收益率进行统计分析得到,该收益率序列的均值为0.000263,标准差为0.019852,表明方差较小,偏度为-0.5067640,小于0,峰度为5.195279,大于3,表明该收益率序列具有“尖峰厚尾”的特点,根据JB值可知,创业板指数收益率序列不服从正态分布。
3.平稳性检验
在上述统计分析的基础上,需要对创业板指数收益率的平稳性进行检验,本文采用单位根(ADF)检验,结果如表1所示。
由表1可知,T值为-27.24295,较大,且P值为0.0000,拒绝原假设,所以创业板指数收益率序列是平稳的。
4.ARCH效应检验
对创业板指数收益率进行平稳性检验后,需要对其进行ARCH效应检验,首先根据AIC准则确定利用AR(1)模型对创业板指数收益率进行自回归,其次运用ARCH-LM对其残差序列进行检验,结果如表2所示。
由表2可知,统计量的伴随概率均为0.0000,所以拒绝原假设,即创业板指数收益率序列存在条件异方差性。
四、实证分析
GARCH族模型能够用来分析波动集群现象和解决时间序列中的条件异方差性,所以本文运用GARCH族模型进行研究。
1.建立GARCH(1,1)模型
本文采用GARCH(1,1)模型对样本进行估计,得到的均值方程和方差方程如下所示:
通过上述方程可知,GARCH项的Z值和ARCH项的Z值均较大,所以拒绝原假设,说明GARCH项和ARCH项的系数均具有显著性,且两系数之和即α+β=0.9930,小于且接近于1,满足模型的参数约束条件,说明创业板指数收益率的波动存在集聚性和持续性。
2.建立EGARCH(1,1)模型
由于GARCH模型中的GARCH项是平方的形式,无法研究正负冲击对创业板指数收益率序列波动性的不同影响,所以本文运用EGARCH(1,1)模型对创业板指数收益率的波动性进行研究,得到的均值方程和方差方程如下:
在EGARCH模型中,μt-1σt-1项的Z统计量较为显著,拒绝系数为零的原假设,说明好消息和坏消息对創业板指数收益率的波动产生不同的影响,即收益率序列的波动具有非对称性,因为
项的系数为负,所以坏消息对创业板指数收益率波动性的影响大于坏消息对其波动性的影响。
五、结论
通过对创业板指数收益率序列进行统计分析和实证分析,我们可以得到以下结论:
第一,创业板指数收益率序列波动存在条件异方差。通过统计检验,发现收益率序列具有“尖峰厚尾”的特征,而通过ARCH效应检验,发现其波动存在条件异方差。
第二,创业板指数收益率序列波动具有持续性,通过 GARCH(1,1)模型发现波动冲击会持续一段时间才逐渐衰减,说明当我国创业板指数受到冲击出现波动时,短时间内无法恢复稳定,自我调节能力比较差。
第三,创业板指数收益率序列波动具有非对称性的特点。通过EGARCH(1,1)模型发现,坏消息对创业板收益率序列波动性的影响大于好消息的影响,也就是说当出现坏消息时,投资者会卖出手中的股票,所以指数收益率会出现波动。
参考文献:
[1]高金莎.基于GARCH模型的中国股票市场波动性研究[J].时代金融(下旬),2017,(07):139~140.
[2]丁扬恺.ARCH模型族在深圳成指中的应用[J].中南大学学报(社会科学版),2012,18(1):131~135.
[3]赵鹏举,海洋,殷燕.基于GARCH-VAR模型的创业板指数收益率波动特征比较研究[J].价值工程,2019,(25):5~9.
作者简介:
1.宋永辉,沈阳工业大学经济学院教授;研究方向:风险投资,国际投融资。
2.许倩,沈阳工业大学经济学院硕士研究生;研究方向:风险投资,国际投融资。

