数学核心素养视域下TIMSS、PISA测试题的比较分析

景菲 高瑞

摘 要 国际数学与科学趋势研究（TIMSS）和国际学生评估项目（PISA）是目前较为成熟的两项国际学生学业成就测试，在教育测评领域有十分广泛的影响。本文从数学核心素养角度对TIMSS、PISA测试题中涉及的数学观念的获得、数学思想的形成以及问题解决的能力三方面素养进行研究比较分析。

关键词 核心素养 TIMSS PISA

中图分类号：G424.74文献标识码：A

1 TIMSS、PISA基本情况介绍

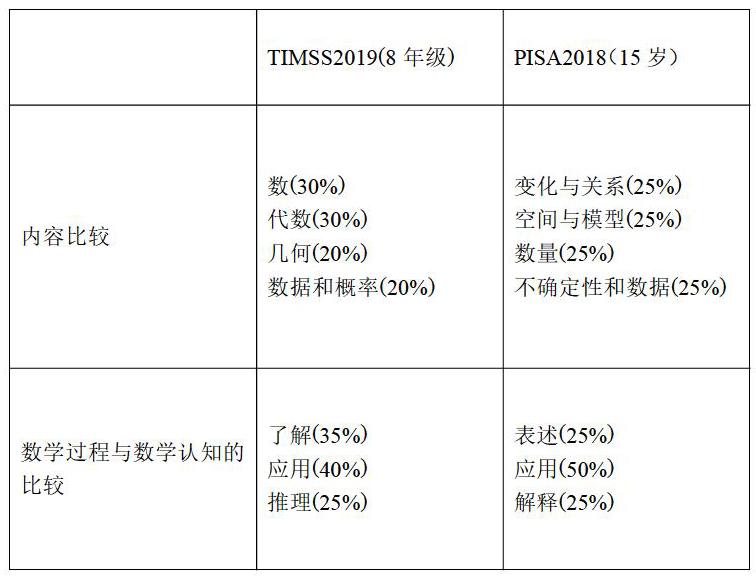
TIMSS、PISA的测试方式相同都采取笔试加问卷的形式，题型都为选择题和问答题。但两者的评价目的不同，TIMSS主要测试学生对课程的掌握程度，PISA则注重对学生实际解决问题能力的测试。因此两者的测评内容有所差异，TIMSS试题与课程具体内容相关，而PISA试题更贴近生活实际问题。换句话说，TIMSS的试题是纯数学的题目，PISA的试题是应用型的数学题目。TIMSS2019与 PISA2018测试评价框架比较如下表：

2 TIMSS、PISA与课程标准数学素养交叉分析

PISA对数学素养的界定为：“数学素养是一种个人需力，学生能够确定并理解数学在社会所起的作用，得出有充分根据的数学判断和能够有效地运用数学。”在PISA中，对于数学素养限定了两个主要方面：数学能力和数学思想;还有两个次要方面：数学课程线和数学情境。（如图1）

TIMSS从三个维度来界定数学素养，分别是：数学内容，数学认知和数学教学目标。（如图2）

TIMSS认为数学教育对学生的发展极为重要，所有的孩子都能从学习与形成坚实的数学技能中获益。因为学习数学可以提高他们解决问题的技能，并培养他们的恒心与毅力。

《标准》提出“在双基教学的基础上，同时也需要关注学生对数学思想、数学活动经验的积累与掌握，培养学生发现问题，提出问题，分析问题，解决问题的能力，让学生养成较好的数学思维品质，不断提高数学素养。”

由此可见，TIMSS、PISA和标准在对数学素养的界定上都涉及了数学观念的获得、数学思想的形成以及问题解决的能力这三方面。

3测试题比较

基于以上对TIMSS、PISA与课程标准数学素养的交叉分析，本文将从数学观念的获得、数学思想的形成以及问题解决的能力三方面，对TIMSS、PISA测试题进行比较分析。

3.1數学观念的获得

数学观念是指用数学的眼光去观察问题，用数学的思维去思考问题的数学意识和习惯。比如，推理意识、抽象意识、化归意识、整体意识、符号意识等。TIMSS2015中涉及“用符号语言表征整数”“日常单位的换算”“运用图表分析数据”等。PISA试题也同样涵盖这些内容，但试题对学生的考查要求更高。下面对具体试题作举例分析。

例1：下列哪个算式的答案更接近的得数？

A、 520    B、525     C、1020      D、1025

该题为TIMSS2015测试题，属于“数”的领域，考查了学生的估算能力，以及学生对数字的敏感程度，要求学生具备一定的数感。在难度上并不大，比较基础。

例2：摇滚音乐会：

摇滚音乐会预留了长100公尺宽50公尺大小的长方形场地作为观众席。音乐会的票全部卖光，而且场地挤满了歌迷。下列哪一个数最有可能是出席音乐会的人数？

A 2 000      B 5 000    C 20 000   D 50 000   E 100 000

该题为PISA2006测试题，主要考查学生的估算能力，同时也要求学生注重日常经验的积累，需要学生大胆猜想每个观众席位所占的面积，并且涉及到面积公式以及“公尺”单位，该单位对于中国学生来说比较陌生，加大了题目的难度。

3.2数学思想的形成

数学思想是指现实世界的空间形式和数量关系反映到人们的意识之中，经过思维活动而产生的结果。比如，函数方程思想、数形结合思想、分类讨论思想、整体思想、化归思想、建模思想等。TIMSS、PISA试题对数学思想的考查有很好的呈现。下面做具体的举例分析。

例1：▲表示佩特原来有的铅笔数量，金姆给了佩特3支多铅笔。佩特现在有几支铅笔？

A、3▲    B、▲ +3    C、 ▲3    D、3▲

该题为TIMSS2015测试题，题目中用“▲”表示了佩特的铅笔数量，是关于用符号表征未知数的思想。“▲+3”则表示两人的铅笔数量。这相较于字母表示数更加的直观，为之后代数、方程的学习奠定了基础。

例2：书架。

问题：木匠制作一个书架需要以下材料：

4个长木板，

6个短木板，

12个短夹，

2个长夹和

14个螺丝。

现在木匠有26个长木板，33个短木板，200个短夹，20个长夹和510个螺丝，请问木匠可以做几个书架？

该题为PISA2006测试题，涉及了对学生“建模思想”“方程思想”的考查，并且问题是开放式的提问，并没有问你木匠最多可以做几个，留给学生更广泛的答题空间。

3.3问题解决的能力

《课程标准》将课程目标分为四个方面：“知识技能”、“数学思考”、“问题解决”、“情感态度”。而“问题解决”相对于其它三个方面，更具有综合性。本文涉及到的数学问题解决能力，是指学生灵活运用自身数学知识和方法解决数学问题的能力，是学生综合性的数学能力。TIMSS、PISA对学生问题解决能力的测评有很好的体现，下面做具体的举例分析。

例1

如果将图中的绳子拉直，哪个选项最接近它的长度？

A、5cm     B、7cm     C、 8cm     D、9cm

该题是TIMSS2015测评题，是属于“几何”领域中的“测量”内容。该题主要的创新点在于曲线的测量，突出了化曲为直的思想。考查了学生的观察能力，估测能力。

例2：形状。

问题1：上面哪个图形的面积最大？请写出你的理由。

问题2：写出一个估算图C面积的方法。

问题3：写出一个估算图C周長的方法。

該题是PISA2006测试题，是关于周长、面积的计算，与教科书练习中的题目相比，不再是已知物体的长、宽，求周长或面积，而是对弯曲图形周长、面积的估算，考查了学生“估算能力”“观察能力”“数学表达能力”等。

4研究启示

4.1以数学素养为核心，正视测评目的

数学测评的目的是检测学生的学习情况，查漏补缺，完善教学。对学生的评价，应该更加注重学习的过程而不是学习结果，教师在关注基础知识、基本技能的基础上，更需要关注学生的问题解决能力、数学表达能力。同时在教学中渗透数学思想、数学思维也显得由为重要。授人以鱼，不如授人以渔。

4.2生活问题“数学化”

PISA测试题多以生活化的数学问题出现，考查了学生解决实际问题的能力，对学生的要求从解答用数学语言表征的数学问题提高到先将生活问题数学化再进行解答的高度。要求学生具备数学抽象、逻辑推理、数学建模、直观想象等数学核心素养。在教学中，需要加强学生对不同问题表征形式的解决能力的培养。

4.3借鉴国际数学测评方法，将数学素养具体化

国际数学测评更多的关注了学生的数学素养，不管是在测评内容上、测评方法上、测评框架上都是基于学生的数学素养维度，从学生的数学素养出发，设计测评框架、测评内容，让培养学生的数学素养具体化。而且，国际数学测评在关注学生知识掌握程度的同时，还对影响学生学业成就的其它因素进行了深度研究。值得我国在数学测评方面好好学习借鉴。

参考文献

[1] 苏洪雨.PISA和TIMSS视野下的学生数学素养探究[J].数学通讯，2007（09）：1-2.

[2] TIMSS2015MathematicsFramework[EB/OL].http：//timssandpirls.bc.edu/timss2015/frameworks.html.

[3] 冷少华.小学数学问题解决能力培养的研究[D].扬州：扬州大学，2013.