可穿戴式外骨骼康复机械手机构设计与分析

陈建军,王 勇,杨岩江

(合肥工业大学 机械工程学院,安徽 合肥 230009)

0 引 言

目前,国内外针对偏瘫患者手部的传统治疗方法主要是依据神经代偿的可塑性原理对手部进行持续运动训练[1-4],其思想是当脑神经系统损伤后,通过科学合理的康复训练来实现神经功能的代偿,进而促进偏瘫患者手部的康复[5-6]。但是传统的手部康复治疗方法费时、费力,借助机器人辅助进行康复训练已成为发展的必然趋势。康复机器人是机器人技术与康复医学的完美结合[7],也是机器人领域中的研究热点[8-9]。

国内外康复机器人辅助训练多以穿戴式外骨骼康复辅具的形式实现。加拿大西蒙弗雷泽大学研制的一款可穿戴外骨骼[10]和韩国东义大学研制的手功能康复外骨骼[11]整体结构简单、操作方便,但这2种外骨骼均不能进行精确的指节康复训练;德国柏林工业大学机器人研究中心设计开发了一款外骨骼式手部康复装置[12],其外骨骼关节处采用四杆机构,并通过绳索完成驱动转动,满足人手适应性要求,但指节运动规律受使用者指长和佩戴情况影响,不能保持稳定的运动规律,存在对患者手部造成二次损伤的风险；哈尔滨工业大学科研团队根据手指的生理特征和运动学特性研制了2款机械手[13-14],该机械手把齿轮机构和空间杆机构组合在一起,有效处理了指面正压力和人手适应性等问题,但是当调节机械手手指尺寸来适应不同患者时会导致机械手运动规律发生变化;青岛大学科研团队研制了一款指节二自由度外骨骼康复机械手[15],但未考虑拇指的康复训练和人手关节运动瞬心偏离问题。

针对上述问题,尤其针对关节运动瞬心重合和指节长度调节问题,本文设计了一种无滑移现象且尺寸可调的可穿戴式外骨骼康复机械手。

1 康复机械手机构设计

手部在进行握拳和伸展动作时,除拇指外其余4指的远端指间关节(distal interphalangeal joint, DIP)和近端指间关节(proximal interphalangeal joint, PIP)各拥有1个自由度,掌指关节(metacarpophalangeal joint, MP)各拥有2个自由度；拇指指间关节(IP of thumb)和拇指掌指关节(MP of thumb)各拥有1个自由度,拇指腕掌关节(carpometacarpal joint of thumb)拥有3个自由度,因此手部共有21个自由度,手部关节如图1所示。

图1 手部关节

1.1 手指运动规律探究

在对正常人手指运动规律进行探究时,采用P3015系列霍尔角度传感器采集数据,通过试验数据得出不同人手指在自由屈伸运动时的统一耦合运动规律。角度信息采集装置模型和试验如图2所示。

图2 角度信息采集装置模型和试验

试验时,选择6位健康成年人进行采样,采样频率为2 000 Hz,对同一个被测者测量4～6次,每次测量时间为10 s,被测者指节屈伸周期限制为2～3 s。数据采集完成后,将所有被测者的参考运动周期调节成2 400个采样点为1个周期,得出原始综合曲线,汇总后进行曲线拟合。根据采集的数据分析,规定手指3个关节弯曲的最大角度为max{θMP,θPIP,θDIP}={50°,90°,30°}。

在Matlab曲线拟合工具箱里,对MP关节角度随采样点的变化情况采用高斯函数进行拟合,对MP-PIP和PIP-DIP关节角度采用二次多项式函数拟合。相关系数依次为0.923 5、0.942 8、0.956 5,将MP关节角度随采样点的变化情况转化为随时间的变化情况,拟合函数为:

(1)

其中,a1=50;b1=T/2;c1=T/3.488;p1=0.036;p2=0.004;p3=-0.026 6;t为在指节摆动周期T内的任意时刻。MP、PIP、DIP关节角度的拟合运动曲线与原始综合曲线的对比如图3所示,其中蓝色、绿色、红色曲线分别对应PIP、MP、DIP关节角度的变化。

图3 PIP、MP、DIP关节角度的综合曲线与拟合曲线的对比

1.2 手指部分机构设计

外骨骼机械手采用手背覆盖式设计,关节转动处采用瞬心投影机构,指节处采用平行四杆机构。机械手手指背面设计成2类连杆机构驱动的形式,并通过电机实现五指统一驱动。

为解决运动时人手与外骨骼的相对滑移现象,在关节转动处采用瞬心投影机构。瞬心投影机构原理及模型如图4所示。

图4 瞬心投影机构原理及模型

杆件ABCD为平行四杆机构,E为AC延长线上一点,在平行四杆机构ABCD运动时,E点会绕BD延长线上某点F做圆周运动,其中虚拟杆件EF与AB、CD平行且相等,设计时将F点投影到手指运动关节上,即可解决外骨骼带动手指运动时瞬心无法重合的问题,从而消除滑移现象。当手指通过绑带固定到瞬心投影机构上,手指便可以和机构上的杆件l5成为一个整体,杆件l4通过推动与l5连接的铰接点E绕瞬心点F圆周转动,使运动过程中手指关节转动中心和机构转动中心始终重合。为满足改变杆长而不改变机械手运动规律的要求,在指节处采用平行四杆机构,使外骨骼和人手对应指节相适应,从而投影瞬心。平行四杆机构原理及模型如图5所示。

初始指节长度对应的平行四杆机构为O-A-B-C-D,按照指节长度调整后增加距离h,对应将平行四杆机构调整为O-A-B′-C′-D,连接驱动杆件l1的长度和初始角度不发生变化,并且下级耦合运动连杆l2同样移动到l2′处,整个过程等幅改变杆件AB、CD杆长而不改变杆件AD、BC杆长,结合平行四杆机构对边等速变化的特点,改变后平行四杆机构的运动规律并不发生改变,从而整个机构的运动规律不发生改变。

将机械手手指背面设计成2类连杆机构驱动的形式,使每根手指在空间中拥有2个自由度,当患者进行手部训练时,2类连杆机构互不产生影响。为了保证使用者手指在正常训练中不会和机构杆件产生干涉,手指部分设计为四连杆机构耦合运动的形式,驱动杆件均设置在外侧。

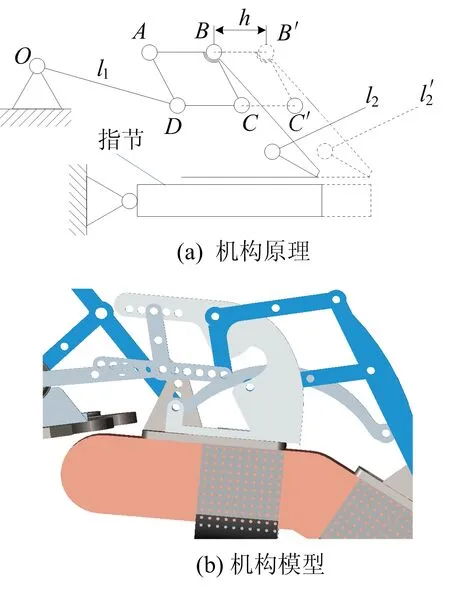
图5 平行四杆机构原理及模型

指节二自由度运动简图及模型如图6所示。

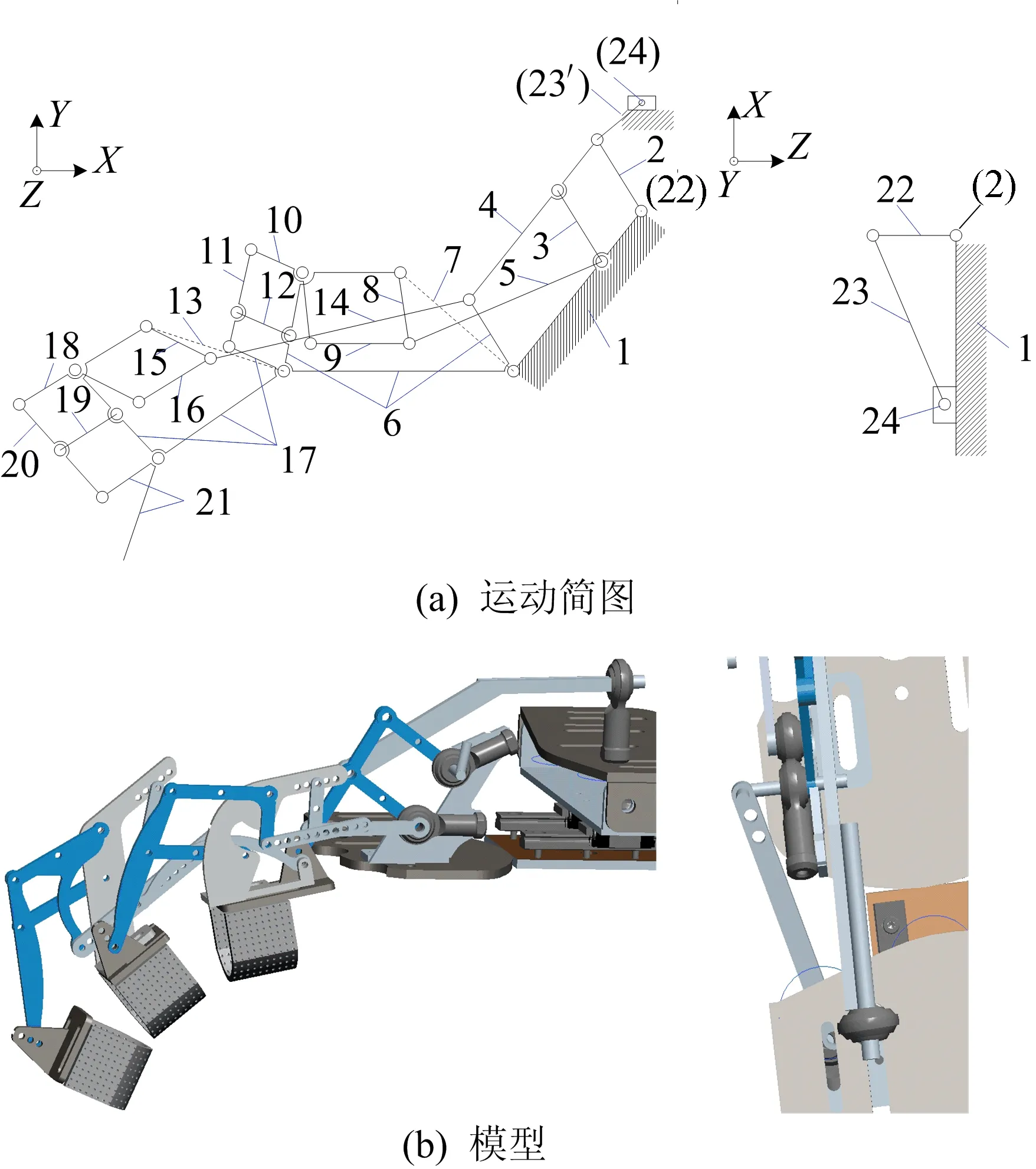
图6 指节二自由度运动简图及模型

图6中,左侧为五指屈伸自由度的运动简图及模型;右侧为四指掌指关节或大拇指腕掌关节摆动自由度的运动简图及模型。

在第一类连杆机构中,四连杆机构依次耦合,图6中，虚线为等效的虚拟杆件7、杆件13,连杆6、连杆17、连杆21作为四指分别代表近节指骨、中节指骨、远节指骨,作为拇指分别代表掌骨、中节指骨、远节指骨,在样机中覆盖在对应指骨外侧。杆件5、杆件14作为第一类连杆机构中的传力连杆,将运动从上一级指骨传递到下一级指骨,从而完成指节之间的耦合运动；杆件6、杆件9、杆件16、杆件17作为第一类连杆机构中的长度调节连杆,可以根据每个人的手指情况进行长度调节；杆件4和杆件6、杆件11和杆件17、杆件20和杆件21为第一类连杆机构中的瞬心投影杆件。

因为可动杆件数为11,低副数为16,高副数为0,所以机构在X-Y面的屈伸自由度为:

F=3n-2pL-pH=1

(2)

同理机构的X-Z面为曲柄滑块机构,摆动自由度为1。因此,对于一根机械手指,在运动空间中通过滑块的驱动就可以拥有2个自由度。

2 康复机械手机构优化

将人手和外骨骼康复机械手的各个指节进行对比分析,通过数学建模和Matlab软件对中间闭链机构和曲柄滑块机构进行杆件尺寸和初始位置优化,根据四杆机构和摆杆机构之间的角度变化比例关系确定远、中、近节指骨的运动关系。

2.1 近节指骨中间闭链机构优化

近节指骨通过中间闭链机构将运动传递到中节指骨,其原理如图7所示。其中,l1为机架;l2为从动件;l3为中间连杆;l4为主动件。4个杆件的长度和相互组成的初始角度决定其传递的效果。

图7 近节指骨机构原理

整个优化过程将β1限制在0°～90°之间,在运动过程中,主动角α1与从动角β1的转向一致。在设计过程中受结构尺寸限制,首先要确定机架l1的杆长。在Matlab软件中联合使用循环函数和优化函数fmincon优化曲柄l2的杆长,再优化主动初始角α1、从动初始角β1和摇杆l4的杆长，即可确定近节指骨传力四连杆的初始位置和转动关系。其中连杆l3的长度通过初始角确定,即

(3)

在此四杆机构中,优化的参数是曲柄、连杆、摇杆的长度。在实际运动过程中主动角α1和从动角β1的角度变化量应保持为(1)式中的函数变化关系,输出对应函数的传动比,通过一定范围内的初始角迭代,对比每对初始角情况下实际角度变化的方差,最终确定最优初始角,继而确定四杆机构的初始位置。其中主动角α1、从动角β1的计算公式为:

(4)

联立(3)式、(4)式得到β1关于α1变化的方程,简写为:

β1=f(α1)

(5)

通过建模分析,取机架长度l1=43.50 mm。再通过Matlab软件编程,最终确定出最优主动初始角α10=46.2°,最优从动初始角β10=90°,最优曲柄长度l2=14.00 mm,最优摇杆长度l4=26.27 mm,最优中间连杆长度l3=41.55 mm。通过数学建模得到的MP-PIP关节角度仿真拟合对比曲线如图8所示。

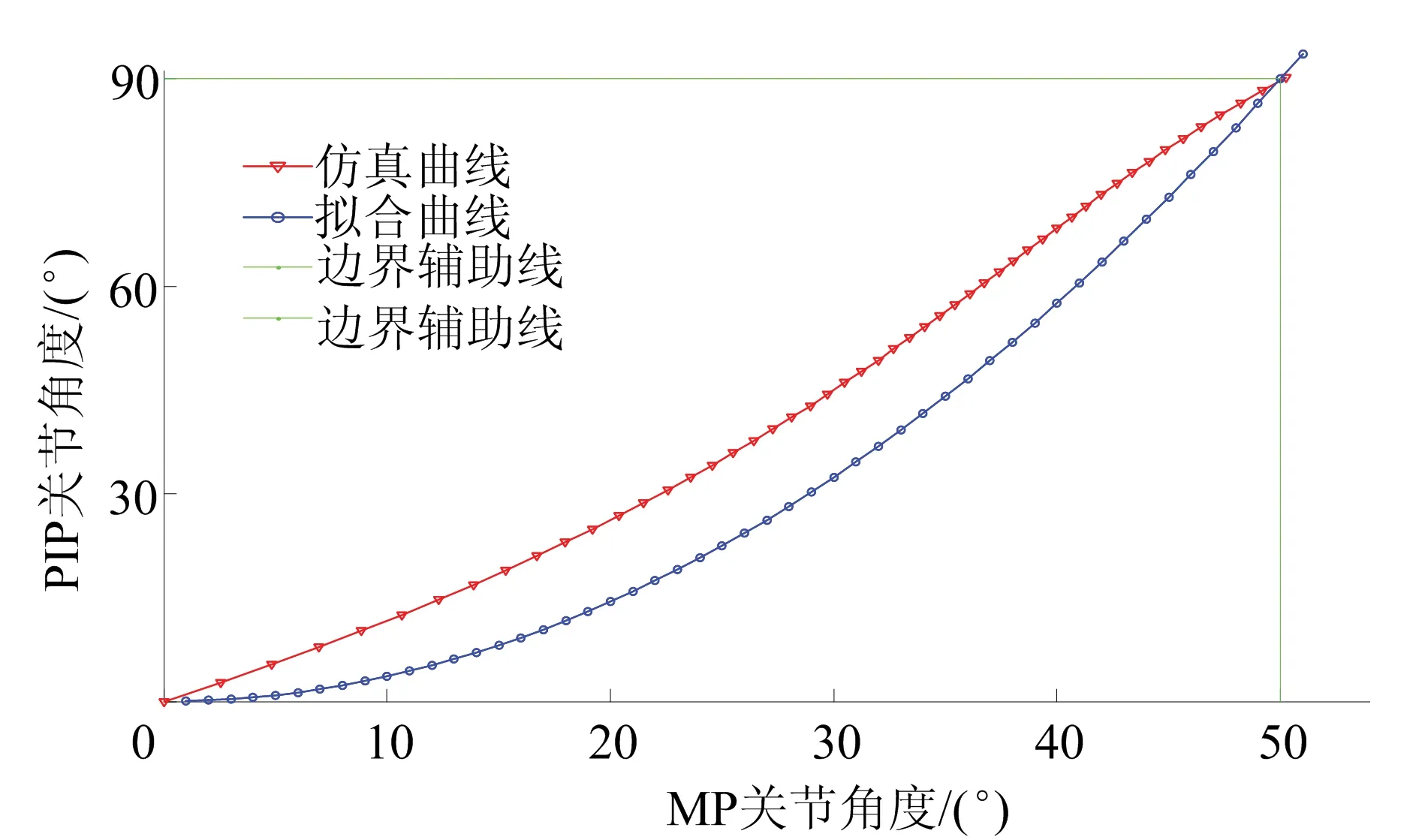
图8 MP-PIP关节角度仿真拟合对比曲线

优化出的从动角β1的角度变化标准差SD=7.561 8。

2.2 中节指骨中间闭链机构优化

中节指骨尺寸优化重复近节指骨的优化操作即可,可得β2关于α2变化的方程,简写为:

β2=f(α2)

(6)

其中，前后运动传递的桥梁是Δα2=Δβ1。通过PIP-DIP拟合函数确定角度耦合关系,并基于角度耦合关系进行建模分析,取机架长度l1′=50.155 mm。再通过Matlab软件编程,最终确定最优主动初始角α20=56.15°,最优从动初始角β20=30°,最优曲柄长度l2′=36.00 mm,最优摇杆长度l4′=34.62 mm,最优中间连杆长度l3′=46.78 mm。通过数学建模得到的PIP-DIP关节角度仿真拟合对比曲线如图9所示。优化出的从动角β1的角度变化标准差SD=8.761 2。

图9 PIP-DIP关节角度仿真拟合对比曲线

2.3 MP双自由度曲柄滑块机构优化

MP关节杆件尺寸的选择要结合摆动部分的滑块移动量来确定,选取导程为14 mm的丝杠。

MP关节摆动机构原理如图10所示。根据图10中2个三角形的尺寸关系可得:

(7)

由(7)式得出r、l关于h、Δh的关系式为:

(8)

联立得θ关于Δh的方程,简写为:

θ=f(Δh)

(9)

由于受结构上的限制,取机架长度h=55 mm,曲柄r的长度在10～25 mm范围之间,基于人手摆动角度,取摆角θ=20°,考虑到滑块前进距离和误差补偿,滑块位移Δh取在10～15 mm范围之间,试验时根据实际情况选定位移Δh后再判断所得曲柄r的长度是否在允许范围内,最后确定连杆l长度即可。

图10 MP关节摆动机构原理

MP关节屈伸机构原理如图11所示。

图11 MP关节屈伸机构原理

由图11可得:

(10)

其中，γ1、γ2分别为前、后2个位置的曲柄滑块机构传动角。由(10)式可以确定唯一一组解(γ1,γ2,r′,l′),为使机构拥有较好的传动性,最小传动角γmin≥45°,最大传动角γmax≤135°,受结构影响,高度差取m=44.5 mm,水平初始位置h′=63 mm,滑块位移量Δh和摆动部分相同,初始角取α=105°,MP关节最大转动角度θ′=50°。若取Δh=10 mm,通过数值解计算可得曲柄r′=24.6 mm,连杆l′=87.1 mm,传动角γ1=88.77°,γ2=48.05°。

3 建模与仿真分析

通过Pro/E软件建模分析,可以得出瞬心投影机构能将机构的转动中心投影到人手转动关节上。当不同人手指节长度不同时,通过改变对应平行四杆机构的杆长,能够达到改变杆长而机构屈伸角度变化规律不变的要求。康复机械手单根手指弯曲运动模型如图12所示,摆动运动模型如图13所示。

图12 单根手指的弯曲运动模型

图13 单根手指的摆动运动模型

将模型导入ADAMS软件中进行运动学仿真分析。把手指部分定义为刚体,参考人体密度将密度设置为1.06 g/cm3,机械手外骨骼部分材料设置为铝合金,机械手杆件和手掌部分材料设置为不锈钢。在ADAMS软件中三指节质量、体积、惯性张量信息见表1所列。

表1 三指节模型信息

各参量设置好之后导入到ADAMS软件中,得到的单根手指模型如图14所示。

图14 单根手指ADAMS模型

通过运动学分析,得到的手部康复外骨骼三指节运动轨迹如图15所示,其中设置坐标点(0,0)为MP关节坐标点。从图15的仿真轨迹曲线可知，手指在摆动时具有一定的耦合关系。

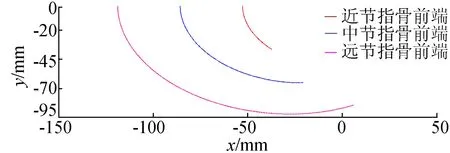
图15 康复外骨骼三指节运动轨迹

通过整周期屈伸分析,得到的三关节弯曲角度曲线如图16所示。手指在伸展状态下开始弯曲,即从180°开始变化。从图16可以看出,ΔθMP=50°,ΔθPIP=90°,ΔθDIP=30°,变化趋势也与图3中三关节角度变化的拟合曲线相符,保证了患者使用时指节的训练精确性,增加了患者使用时的安全系数。

图16 三关节弯曲角度曲线

4 物理样机试验与分析

物理样机的适应性主要通过2个试验进行验证,即瞬心投影适应性试验和外骨骼指节长度调整适应性试验。

瞬心投影适应性试验主要包括单根手指整个屈伸运动周期的转动中心位置比较。选取食指进行屈伸运动周期分析,通过在计算机上分析辅助线的形式,在试验图片上进行模拟瞬心辅助线标记。食指屈伸运动过程中任意2个位置的瞬心标记如图17所示。

图17 屈伸运动任意2个位置的瞬心标记

图中蓝色、橘色、黑色标记分别为MP关节、PIP关节、DIP关节瞬心投影点,白色为手部指骨主运动链。通过物理样机带动手部转动,验证了手部在屈伸运动中能够保持优良的瞬心重合性,使得外骨骼和人手在整个屈伸运动周期中基本不产生相对滑移。

外骨骼指节长度调整适应性试验主要包括根据不同人手指节长度调节外骨骼指节指长,并在调节后还能够保持瞬心重合性和运动幅值。选取食指进行不同指长使用者的屈伸运动试验,并借助计算机分析由霍尔角度传感器测量出的手指三关节转动角度。

不同受试者使用机械手时的适应性情况如图18所示,通过霍尔角度传感器收集的对应受试者关节角度变化情况如图19所示。其中受试者A身高1.71 m,食指指节长度从MP关节开始分别为46、29、25 mm;受试者B身高1.83 m,食指指节长度从MP关节开始分别为48、30、27 mm。

图18 受试者A和受试者B使用机械手时的适应性情况

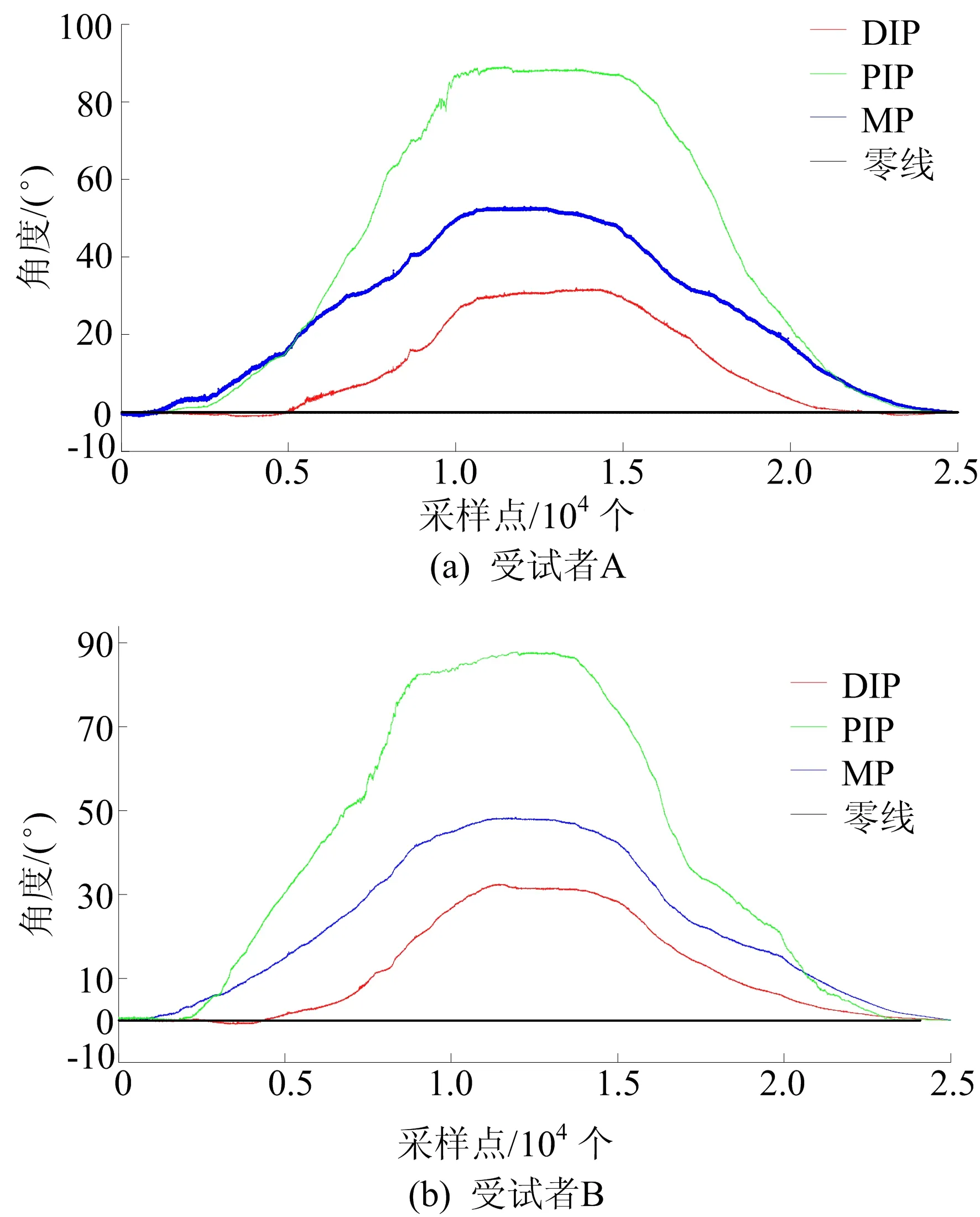
图19 受试者A和受试者B的关节角度变化曲线

由图19可知,受试者A的MP关节、PIP关节、DIP关节实际转动角度分别为52.93°、89.07°、31.82°,受试者B的MP关节、PIP关节、DIP关节实际转动角度分别为48.25°、88.31°、33.29°,与手指运动规律探究中设定的3个关节最大转动角度相差较小,在合理的偏差范围内,并且转动过程中角度的变化基本符合图3中关节角度所拟合的曲线。因此，改变物理样机平行四杆机构的杆长,在适应2位受试者指节长度的同时,外骨骼手指关节瞬心依然能够投影到受试者手指对应关节上,证明了改变外骨骼指节相应杆件长度能够适应不同人手指节长度。

5 结 论

(1) 本文通过分析国内外研究现状,在对人手运动规律进行探究的基础上,设计了一种可穿戴式外骨骼康复机械手。

(2) 对机械手进行总体结构设计,采用瞬心投影机构和平行四杆机构形式,并通过优化外骨骼关节闭链机构,解决了转动部分瞬心投影和指节长度可调节两大难点。依据建模仿真分析,从理论上验证了康复机械手在使用时不会与人手产生滑移现象,调整机械手指节尺寸不会导致机械手运动规律发生改变。

(3) 在物理样机试验中采集试验数据并与手指运动规律探究中得到的拟合曲线相比较,验证了机械手对康复训练的有效性。