考虑历史解的多软件系统动态可靠性分配

张世金,岳 峰,张国富,2,3,蒋建国,2,3

(1.合肥工业大学 计算机与信息学院,安徽 合肥 230601; 2.工业安全与应急技术安徽省重点实验室,安徽 合肥 230601; 3.安全关键工业测控技术教育部工程研究中心,安徽 合肥 230601)

0 引 言

软件是一系列按照特定顺序组织的计算机数据和指令的集合,自20世纪40年代诞生以来,它的快速发展极大地推动了社会的进步。如今,软件的影响力辐射到了整个社会的方方面面,给人们的生活带来巨大便利,同时不可靠软件带来的危害也越来越严重,关于软件可靠性的研究逐渐成为人们的研究重点,软件可靠性优化更是其中的一个重要分支。

软件可靠性优化问题,亦可称为软件可靠性分配问题(reliability allocation problem, RAP),它是指在软件开发的设计阶段,设计人员提前对软件内部的组成元素作出分析,根据相应规则把软件分为更小的组成模块,并据此对软件的基本模块进行可靠性分配,以实现软件开发成本有限的情况下,用户得到的软件可靠性尽可能大的目的[1-2]。

对于RAP的研究已有一些成果。文献[3-4]就软件操作剖面以及历史信息对软件可靠性优化的影响进行了研究;文献[5]认为软件的复杂度应该被考虑进软件RAP中;文献[6]建立基于软件系统层次结构的软件可靠性分配模型,综合用户、项目经理以及软件工程师的观点,利用模糊层次分析法[7]获得各模块的全局权重;文献[8]基于多软件系统层次结构,构建成本约束的系统可靠性最大化模型,并利用Dempster-Shafer(D-S)证据理论[9-10]获得各模块的参数值;文献[11]对软件可靠性增长模型的不确定性进行了量化研究;文献[12]综合分布估计算法与差分进化算法的优点,提出一种混合智能优化算法求解复杂软件RAP。

综合分析已有相关研究成果可以发现,对于软件可靠性分配模型的建立、模型的求解算法等领域,已有较深入的研究,但对于软件动态可靠性分配模型以及其保留历史解信息的核心思想,相关研究成果很少。本文在多软件系统动态可靠性分配模型的基础上讨论模型求解过程中对于历史信息的处理。

1 多软件系统动态可靠性分配模型

多软件系统的层次结构如图1所示。

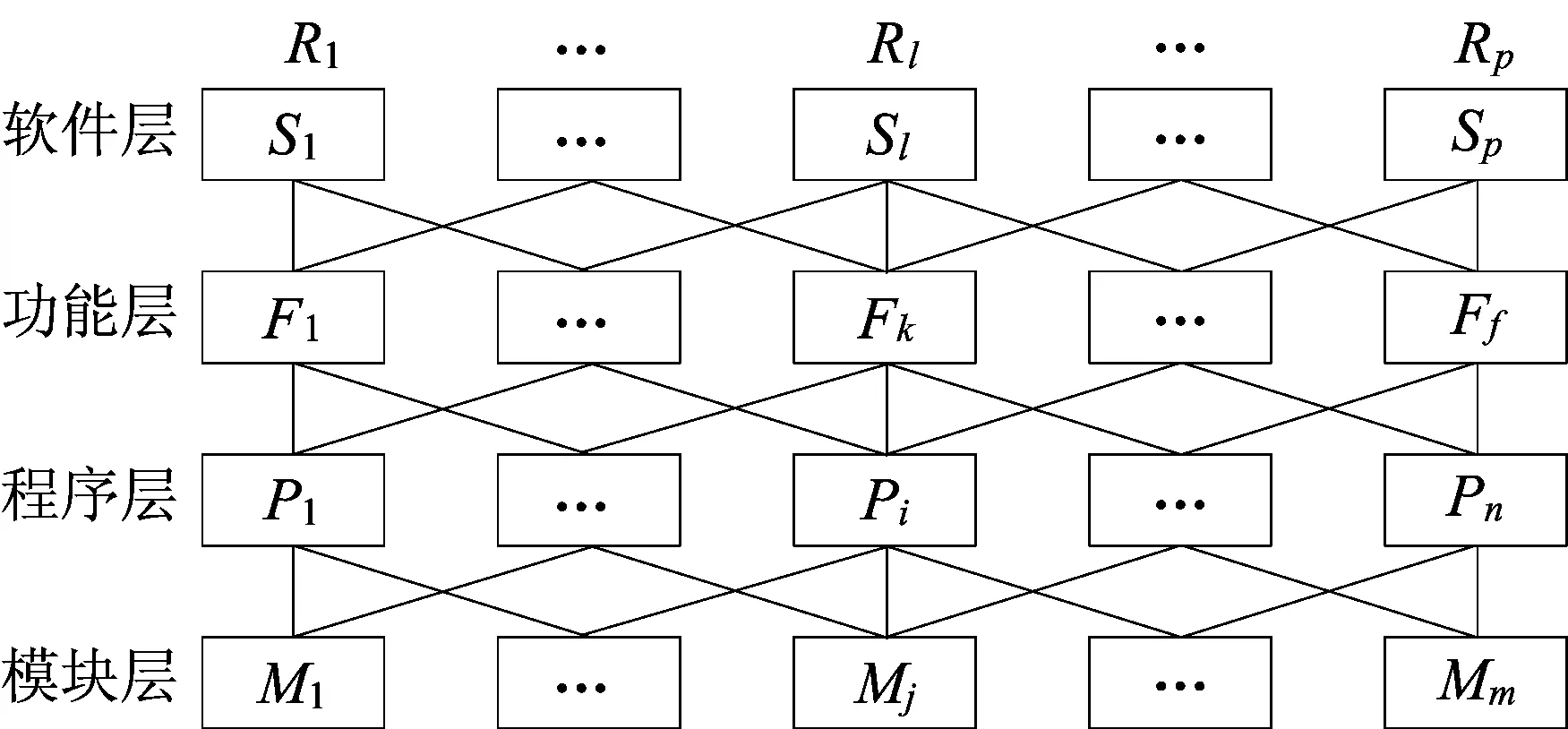
图1 多软件系统层次结构

第1层为软件层,是用户对每个软件Sl可靠性Rl(l=1,…,p)的总体评估。第2层为功能层,Fk(k=1,…,f)表示软件存在若干功能。第3层为程序层,Pi(i=1,…,n)表示功能都由若干程序实现。第4层为模块层,Mj(j=1,…,m)表示每个程序都包含若干模块,这里每个模块是独立的,且只将可靠性指标分配到模块层为止。

软件可靠性程度通过“软件实用性”来衡量。在上述层次结构中,程序层既反映了用户对软件可靠性的观点,又反映了程序员的建议,因此,通常从程序层的视角去研究多软件系统的实用性U,计算公式为：

(1)

其中,wPi为程序Pi的全局权重;rPi为程序Pi的可靠性。由于模块是独立的单元,rPi计算公式为:

(2)

其中,rMj为模块Mj分配到的可靠性。此外,每个模块Mj有一个全局权重wMj。

综合软件系统的层次结构以及“软件实用性”的定义，多软件系统动态可靠性分配模型可表示为:

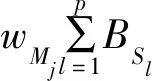
在上述模型中,m的值是动态变化的,即模块数是变化的;目标函数U为整个多软件系统的整体实用性,是各模块可靠性rMj的函数,其中rMj是唯一的未知变量。因为m的值是动态变化的,所以变量集{rM1,…,rMj,…,rMm}也是动态变化的。约束条件(4)式是对模块Mj可靠性的约束;约束条件(5) 式是对模块Mj成本的预算约束;约束条件(6) 式是对软件Sl的成本约束。

2 差分进化算法

差分进化(differential evolution,DE)算法是一种基于群体的启发式搜索算法[13]。主要的进化流程包括种群初始化、变异、交叉及选择。

(1) 初始化种群。在解空间中随机均匀产生初始种群:

i=1,2,…,N;j=1,2,…,D}。

其中,Xi,j(0)表示初始种群第i个个体的第j维;N为种群的大小;D为个体的维数。

(2) 变异。DE算法通过差分策略实现个体变异,常见的差分策略是随机选取种群中2个不同的个体,将其向量差缩放后与原始个体X进行向量合成,生成1个新的变异个体V，即

Vi,j(g)=Xr1(g)+F(Xr2(g)-Xr3(g)),

其中,r1、r2、r3为3个互不相同随机整数;F为缩放因子,是一个确定的常数;g表示该种群处于第g代。

(3) 交叉。交叉操作的目的是随机选择个体,因为DE算法是一种随机算法,所以交叉操作的方法为:

其中,R为交叉概率。通过随机的方式生成新的个体，随机的概率为交叉概率R。

(4) 选择。DE在个体的选择上采用贪婪选择策略,即通过计算原始种群和交叉后的种群相应位置个体的目标函数值来判断个体的优劣。具体操作为:

其中,f(Ui,j(g))、f(Xi,j(g))的大小取决于问题的目标函数。

3 D-S证据理论

D-S证据理论[14]通过合并多重证据从而作出决策,对推理进行合理的解释而达到一定程度的信念。

设UH为变量H可能值的样本空间,则称UH为H的识别框架。H的基本概率分布函数μ满足:

μ:2UH→[0,1];

其中,2UH为UH的所有非空子集的集合;μ(A)表示对A的精确信任度,为集合A的基本概率数。

当来自不同数据源的数据对相同的识别框架提供不同的评估信息时,用于信息融合的合成规则如下。

设μ1(B)、μ2(C)为同一识别框架的2个不同的证据,则有:

其中,A=B∩C;K为归一化常数,用来计算所有非空集合的基本概率之和,可以避免在组合时将非0的概率赋给空集。通过K可以把空集所丢弃的信度按比例分配到非空集上,有效地表示了证据间的冲突程度,其值越大说明证据之间的冲突越大。

4 考虑历史解的动态可靠性分配算法

记多软件系统改变前、后的状态分别为I、Y。多软件系统动态可靠性分配模型的求解步骤如下。

(1) 利用D-S证据理论求出各程序、模块的全局权重。

(2) 利用DE算法对I状态的模型进行求解,直到达到DE的终止条件,记I状态的末代种群为Ii,j(gend)。

(3) 通过相应保留历史解的策略,在Ii,j(gend)基础上产生Y状态求解的初始种群。

(4) 利用DE算法对Y状态的模型进行求解,与步骤(3)的区别在于Y状态的初始种群由Ii,j(gend)产生,而I状态的初始种群随机产生。

(5) 根据目标函数,在Y状态末代种群中选择最优个体作为模型的解。

多软件系统动态可靠性分配问题的核心在于对于历史解信息的保留,体现在该模型求解的步骤(2)与步骤(3)。在该模型中,利用DE算法对当前状态进行求解时,DE算法的初始种群产生于历史状态。相比于随机产生的初始种群,包含历史解信息的初始种群显然距离理想种群更近,这有助于模型的求解。

本文以缩短DE算法初始种群与理想种群的距离为目标,提出3种保留历史解的策略。

策略1 提升DE算法历史种群的进化水平。历史种群的进化水平直接决定了历史解所包含信息的质量,从主观来看历史种群进化的水平越高越具有被保留的价值,但历史种群的进化水平与保留历史解策略之间的具体关系需要实验的验证。

策略2 选择合适的保留历史解的比例。考虑到DE算法的性质,在种群进化至相当水平后,种群中个体间的差异逐渐减小,这可能会对新的初始种群的产生带来负面的影响。

策略3 根据目标函数对DE算法历史种群的个体执行排序操作。DE算法种群的个体存在好坏之别,选择更优的个体作为历史信息保留下来会让保留历史解的策略效率更高。

5 仿真实验设计与求解

设计仿真实验验证本文提出的3种保留历史解的策略。

5.1 实验设计

本次仿真实验中,多软件系统改变前、后的状态分别记作T1与T2。状态T1、状态T2多软件系统的层次结构如图2所示。

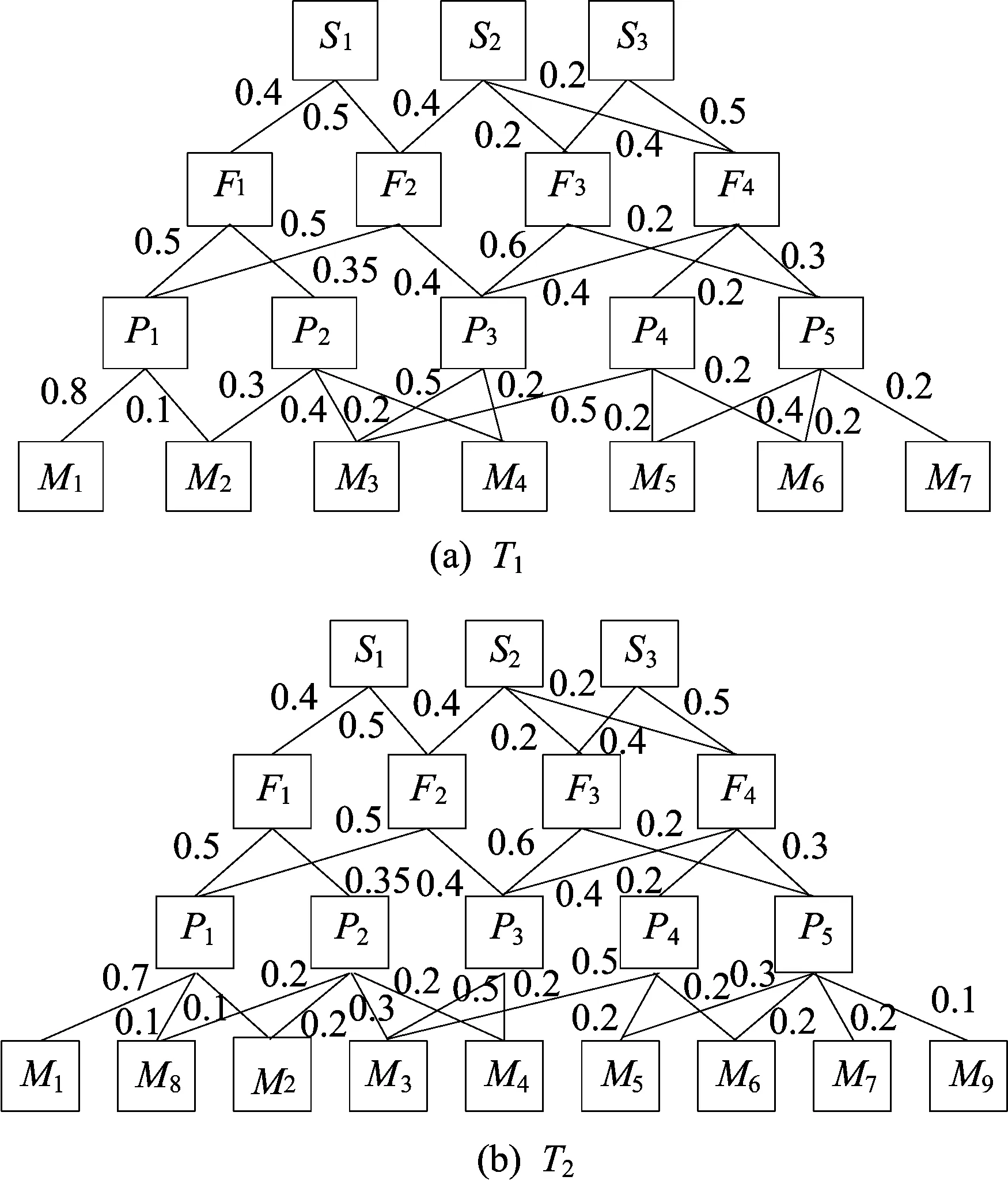
图2 状态T1、状态T2层次结构

与状态T1相比,状态T2的程序P1、P2新增了模块M8,程序P5新增了模块M9,相应的P1、P2及P5关联模块的权重也发生了改变,而P3、P4关联模块的局部权重没有变化。

5.2 实验结果

实验中S1、S2及S3的预算分别为250、450、300,DE算法的R=0.5,F=0.94,种群规模为60。

(1) 策略1仿真。控制DE算法历史种群进化水平的模型求解结果如图3所示。

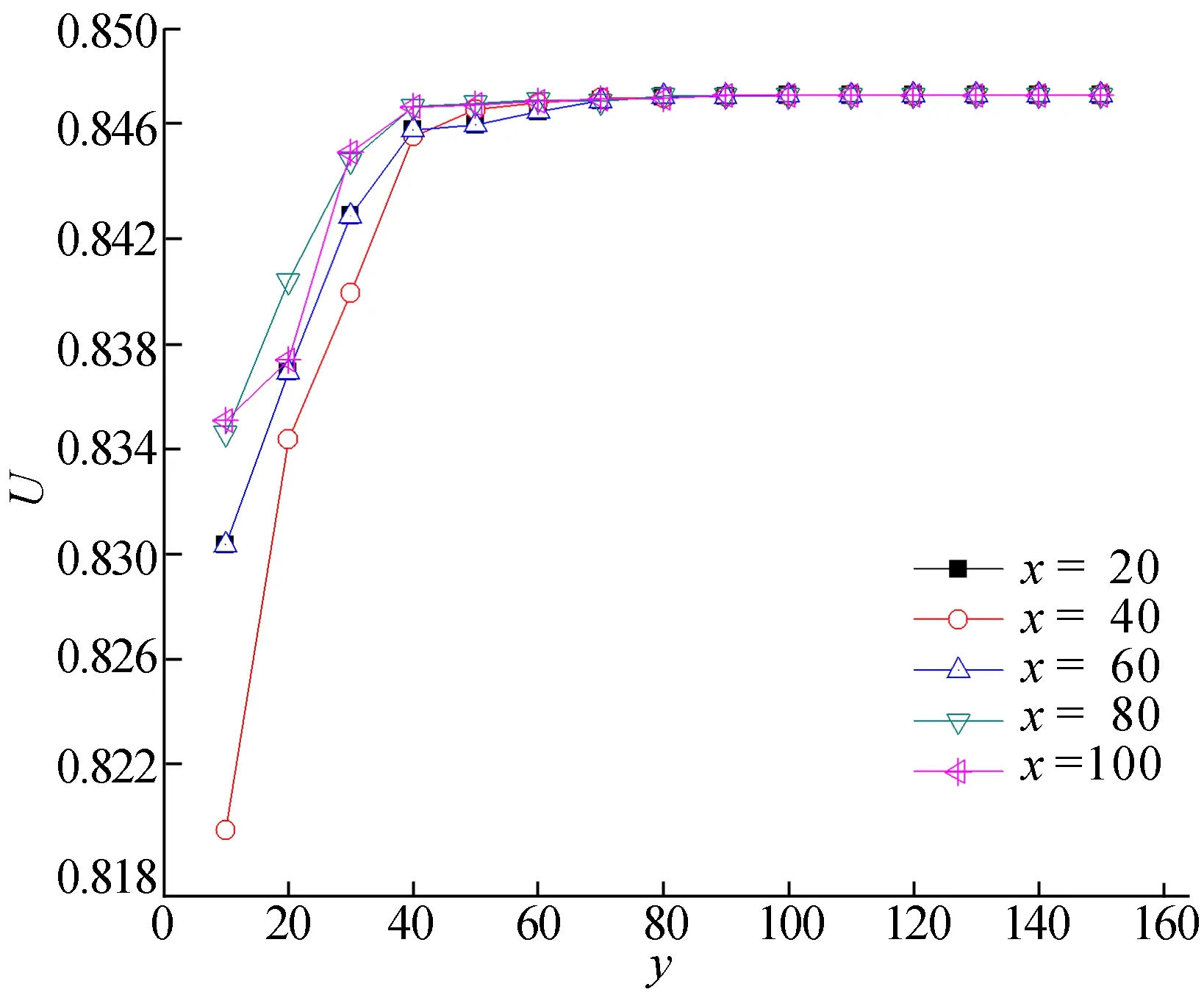
图3 控制DE算法历史种群进化水平的结果曲线

图3中,横坐标y为状态T2DE算法进化的代数;纵坐标U为对应条件下多软件系统的可靠性;x为状态T1的进化代数。

从图3可以看出,状态T1进化代数越高则最终的结果曲线越好,在y值较小时更加明显,此现象表明历史种群的进化水平对于保留历史解的策略确实有影响,历史种群进化水平越高，保留历史解的效果越好。

(2) 策略2仿真。控制保留历史解比例的模型求解结果如图4所示。

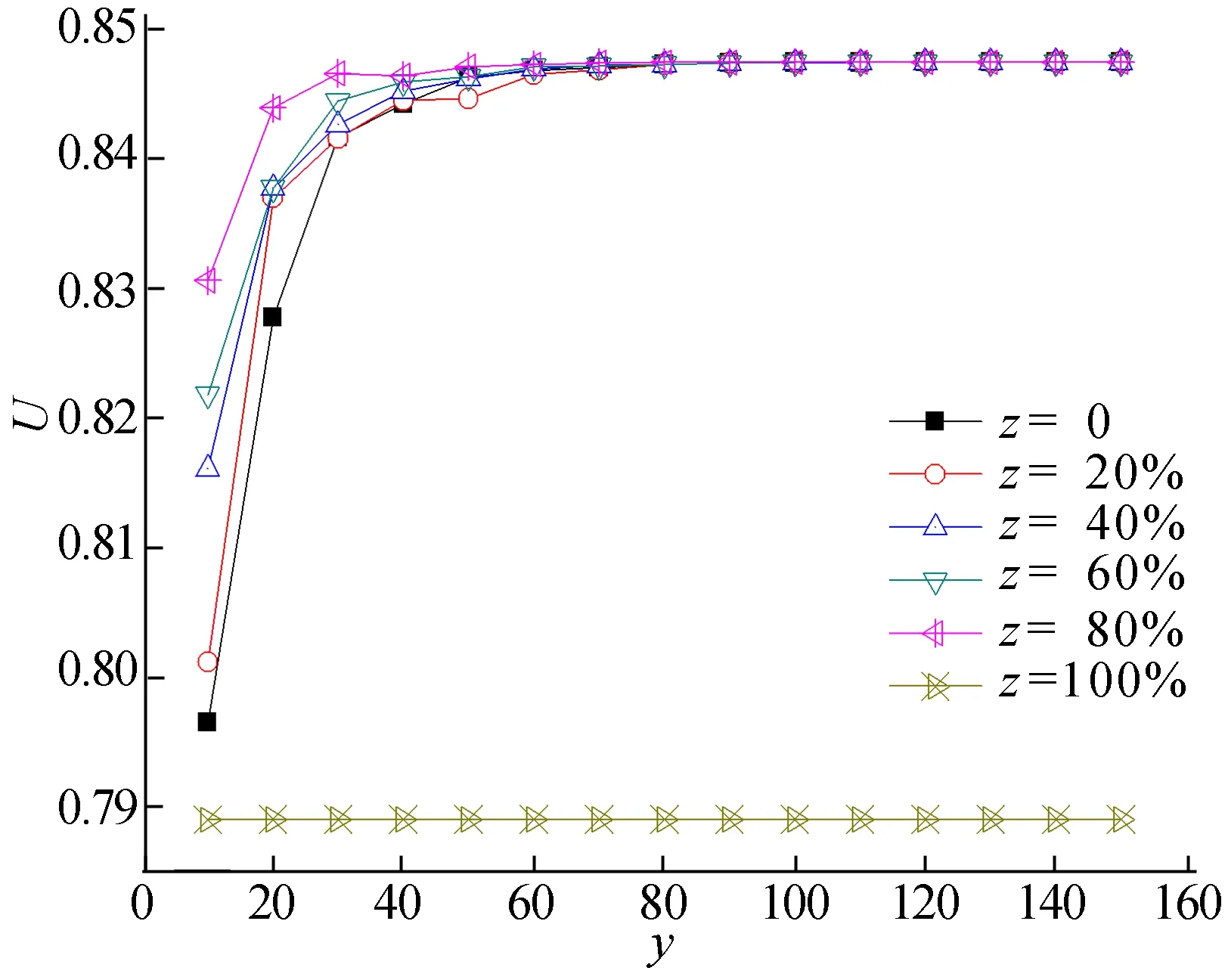
图4 控制保留历史解比例的结果曲线

图4中,z为历史解保留的比例。从图4可以看出,z分别取0、20%、40%、60%、80%时,结果曲线大致呈z越大曲线越靠上的趋势,尤其是在y值偏小的情况,虽然相邻曲线比较接近,但是z从0增至80%,曲线结果慢慢变好的趋势十分明显;z=100%的曲线并不遵从z越大结果曲线越靠上的规律,而是一条几乎平行于横轴的直线，这是由于当保留历史种群的全部个体去产生新的初始种群时,初始种群从一开始就陷入了局部最优,于是就有了z=100%时结果曲线为一条接近平行于横轴的直线的现象。

通过以上仿真实验可知,通过提高保留历史解的比例可以提升模型求解的效果,但提高保留解的比例并不是毫无节制的,本次仿真实验中保留解的比例上限在80%左右,当比例超过80%时模型的求解效果会急剧变差,甚至会让DE算法失效。

(3) 策略3仿真。对DE算法历史种群中的个体执行排序操作后的模型求解结果如图5所示。

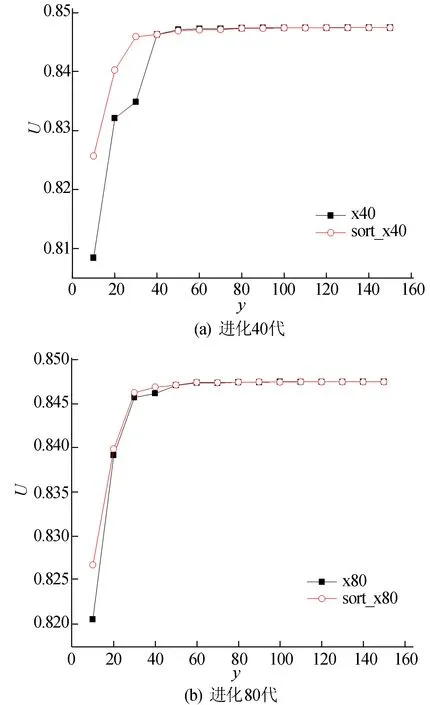
图5 排序操作后的结果曲线

图5a中,x40、sort-x40的曲线分别为对DE算法的历史种群不执行和执行排序操作条件下的结果曲线,状态T1进化了40代。

图5b中,x80、sort-x80的曲线分别为对DE算法的历史种群不执行和执行排序操作条件下的结果曲线,状态T1进化了80代。

从图5a可以看出,sort-x40的结果要好于x40的结果,这表明对DE算法历史种群的个体执行排序操作对于提升模型的求解效果有所帮助。从图5b可以看出,x80与sort-x80的曲线结果十分接近,这是由于当状态T1进化至80代时,DE算法的种群接近收敛,此时种群中的个体差异不大,因此排序操作对其影响不大。

通过以上仿真实验可知,对历史种群的个体进行排序操作对保留历史解的策略有正面的影响,历史种群进化水平越低，此影响越明显,当历史种群进化至几乎收敛时，此影响几乎可以忽略不记,因此可以视历史种群的具体进化情况选择是否执行排序操作。

6 结 论

本文针对多软件系统动态可靠性分配模型求解过程中的保留历史解策略进行了研究,提出3种有效的保留历史解策略:① 提升进化算法历史种群的进化水平;② 合理选择保留历史解的比例;③ 根据目标函数对进化算法历史种群的个体执行排序操作。仿真实验结果证明了本文策略的有效性。虽然仿真实验得到了预期的效果,但本文关于保留历史解策略的研究还很有限,后续研究方向是找到关于保留历史解策略更加系统的方法。