飞机结构强度试验安装顺序的遗传算法优化

张洋洋， 于哲峰

（上海交通大学航空航天学院，上海200240）

0 引 言

飞机研制过程中，地面结构强度试验是重要的一环，包含部件级试验和全机试验，种类非常多。常见的有起落架静力试验，机翼、平尾和垂尾静力试验，机身或某段机身静力试验等等。由于试验件不同，每项试验都有各自的特性。即使是同一项试验，如起落架试验，不同新机型其起落架也千差万别，需要为各自起落架设计专用加载、支持夹具，专用试验方案和安装顺序，且每项试验通常只会做一次。大型结构或全机静力试验［1］通常需要大量的不同安装、换装工作，涉及试验件、支撑框架、加载夹具、作动器、传感器等。因此想要建立一个相对通用的安装顺序优化算法难度较大。

结构强度试验安装顺序优化本质上属于装配顺序优化问题［2-4］，随着装配零件个数的增多，装配顺序会出现组合爆炸问题［5］。对于此问题，文献［6-10］中利用遗传算法优化装配顺序；文献［12-14］中利用蚁群算法优化装配顺序，文献［15-17］中利用粒子群算法优化装配顺序。以上3 种智能算法均可解决组合爆炸问题。

多个领域的装配顺序优化问题已被较好地解决。苏强等［18］提出装配角度、装配方向、装配稳定性和重定位次数4 个指标构建的装配顺序优化模型，用疫苗自动获取的免疫遗传算法求解，并提出4 种免疫疫苗用于提升算法运行效率，快速有效地找出了船舶工段的装配顺序。张丹等［19］针对航天产品装配顺序优化问题，提出了基于粒子群遗传算法。黄洁等［20］提出了带约束的多目标遗传算法来实现阀门装配序列规划，对不满足约束的顺序通过增加惩罚来减小适应度函数值，但仍在交叉、变异后进行了约束条件判断手动排除。李原等［21］基于遗传算法对飞机机翼产品进行了装配序列优化。Lu 等［13］提出了一种利用蚁群算法来解决面向装配线平衡的装配顺序问题。但鲜有人将上述优化算法应用于飞机结构强度试验的安装顺序中。

本文结合飞机结构静力试验的安装特性，提出了相应的适应度函数和量化评价安装顺序的方法，最终构建了一种多目标、多约束的遗传算法，实现了实验安装顺序的优化。

1 结构试验安装顺序优化模型简化

飞机结构静力试验通常需要安装支持夹具、加载夹具、试验件、作动筒、立柱、横梁、地脚螺栓、位移传感器、杠杆以及连接液压控制阀、应变计等传感器的线缆等工作。

为适当简化模型，初步按以下4 方面约定进行建模。①作动筒有时需安装在立柱上，有时需要安装在基座上，可将后者的作动筒与基座视为一个安装部件；②支持夹具本身通常也有许多零件组成，在出厂时通常未必按安装好的状态交付，但由于支持夹具通常为一个整体，可将支持夹具的众多零件简化为一个安装部件；③位移传感器通常在试验全部安装结束后再安装，对此项可不进行安装排序；④应变计通常在整个安装过程之前已在试验件上粘贴完毕，对此项也可不必参与排序。

由于试验件不同，每个静力试验方案、安装都可能存在很大差别，需要针对每个试验各自的特性提炼出可简化的安装部件来进行排序。

需要排序的安装部件确定后，给出各零部件编号、名称、重心坐标、安装各零部件所需工人数量及安装各零部件所需工具。

2 适应度函数的设计

2.1 适应度函数的影响因素

结合飞机结构试验通用的特性，对于不同的装配顺序的适应度值可以从以下5 个因素的适应度得出：

（1）装配操作的连续性。该因素与安装工人位置变动有关，可用安装完全部零部件后工人在水平面所走的路程来表示，即在某种排序下各零部件重心之间的距离和，该和越小，则适应度值越小。该因素的适应度值用F1表示。

（2）试验件安全性。即为了避免安装过程中对试验件的碰撞、工具高空坠落砸到试验件等因素，试验件越靠后安装，则认为试验件的安装安全性越好，通过试验件在安装顺序中的排位，排得越靠前适应度值越高，越靠后适应度值越低。该因素的适应度值用F2表示。

（3）装配工人的变动次数。即安装每个零部件需要的装配工人数量变动量越大，适应度值越大。该因素的适应度值用F3表示。

（4）高空作业量。即工人爬上爬下的次数越少，则适应度函数值越小。分别计算相邻两个零部件重心坐标（高度）的差值，累计叠加后的值越大，则适应度函数值越大。该因素的适应度值用F4表示。

（5）使用装配工具的连续性。即安装完一个零部件后，装下一个零部件时不需要更换安装工具，可省去重复找工具的时间。令更换工具次数越少，适应度函数值越小。该因素的适应度值用F5表示。

对以上5 个因素分别定义各自权重，最终某一安装顺序的总适应度值为以上5 个因素的适应度值相加。飞机结构强度试验安装顺序优化问题可简化为求适应度值最小值的问题。总适应度值（装配难度）计算式为：

式中：ωi为权重系数，根据工程经验确定。

由于每个试验都有其特殊性，可在单独总结试验特殊性因素加入到适应度函数中。

2.2 约束条件与处理

实际安装过程中，某些零部件存在必须的先后安装顺序，因此为了使得出的解更具有实际意义，还需对模型增加安装顺序的约束条件，本文提出了以下4 个约束条件：①立柱要在高空横梁安装之前安装；②试验件需要在支持夹具之后安装好；③试验件需要在高空横梁之前安装；④杠杆系统需要在试验件之后安装。当某一代种群中的一组排序出现不满足安装顺序需要满足的条件时，即不满足约束条件时，可通过增加惩罚函数的方法，即在该序列的适应度函数值的基础上加上一个较大的常数惩罚值，使该序列最终的适应度函数值较大，从而在迭代过程中进行选择操作时大概率淘汰该序列，而不需要在每一步的交叉、变异之后再次进行有效性检验。当所有不满足约束条件的序列在种群中都淘汰后，剩下的就是都满足约束条件的解。该方法结合遗传算法“物竞天择，适者生存”的特点，巧妙地回避了对每一种顺序序列的每一步计算前都需要判断是否符合约束条件的步骤，极大地提高了程序计算效率，简化了程序代码。

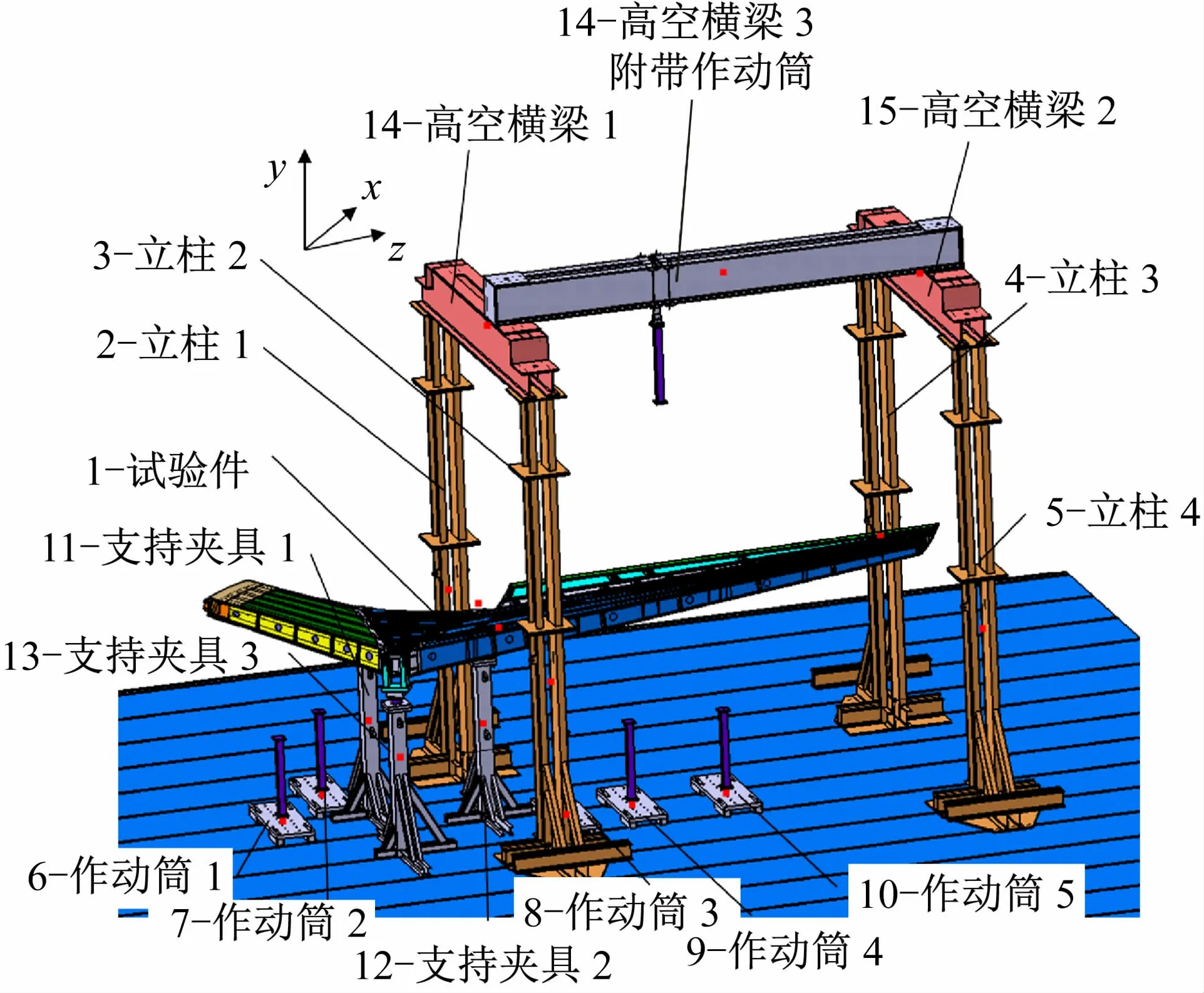
图1 平尾试验安装布置示意图

3 应用算例

以一个平尾结构的静力试验为例，为了使本算例更具代表性，只选取了部分安装组件进行安装顺序的优化。平尾试验安装图如图1 所示。试验件由3 个支持夹具固定，下部有5 个作动器及安装夹具（图中未显示杠杆系统），上部有1 个作动器，施加向上的载荷；而为了实现向上加载，使用4 个立柱和3 个高空横梁固定上部的作动器。

3.1 编码与解码方法

取本实验中的17 个零部件分别进行编号，统计各零部件重心坐标，将重心点代表各零部件。各件编号、名称、重心坐标、安装所需工人数量及安装所需工具见表1。杠杆系统的x、z 坐标取底下5 个作动筒x、z 坐标的平均值，杠杆系统的y 坐标值（高度值）等于试验件的z坐标值减300。本例中杠杆的安装也需要占用部分工作量，故将杠杆系统也视为需要安装的零部件之一。本程序采用十进制编码，优化程序输出的编码即为1 ～17 的17 个数的排列顺序，1 ～17 分别代表着表1 中17 个需要安装的零部件。

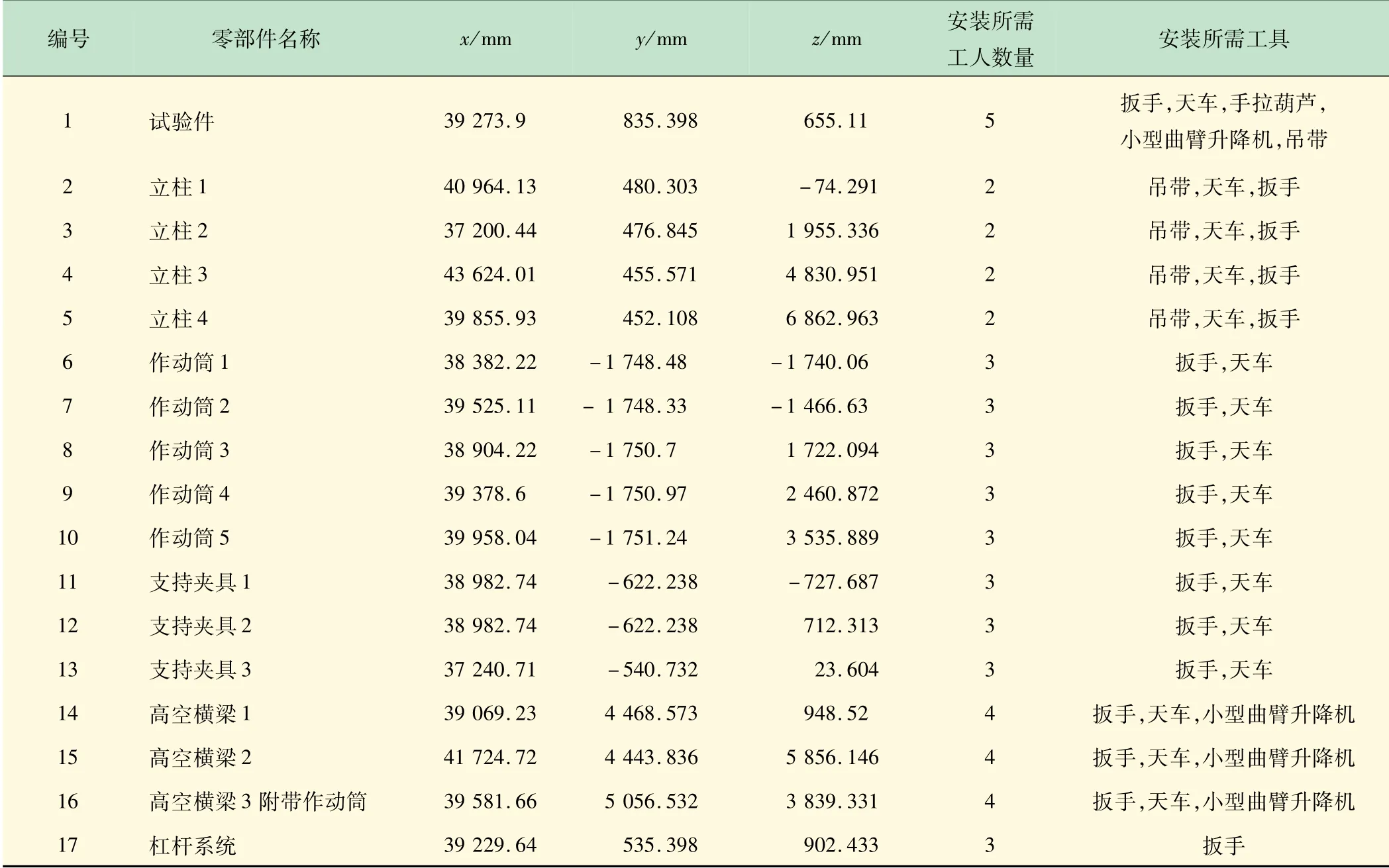
表1 零部件编号、名称、重心坐标、安装所需工人数量及安装所需工具

3.2 适应度函数

本实施例共考虑5 个适应度函数组成因素，即：

（1）装配操作的连续性。分别计算相邻2 个零部件重心在xz平面投影的距离值和，表示安装完全部零部件后工人在xz平面所走的路程。权重值w1为1。

（2）高空作业量。通过分别计算相邻2 个零部件重心y坐标（高度）的差值，表示工人爬上爬下的距离。权重值w2为2。

（3）试验件安全性。具体规则为：若试验件安装排在第i 位，则该项适应度值为（17 000 -i）×1 000，权重值为w3＝1。

（4）装配工人的变动次数。具体规则为将安装每个零部件所需工人数量输入至数组，在某一序列中将每个前后相邻的两个零部件所需工人数相减，再求和得出总的装配工人变动量。权重值w4为1 000。

（5）使用装配工具的连续性。本算例假设安装所有零部件共需要使用5 种工具（扳手、天车、手拉葫芦、小型曲臂升降机、吊带），分别计算安装前后两个零部件所需安装工具不同的数量，求出不同数量的总和，设权重值w5为1 000。

权重选取原则：

适应度函数的5 个组成因素中，第1、第2 个因素为各部件重心坐标的距离和。由于试验3 维模型通常在catia 中建立，采用mm 为单位，工人来回走过的距离和通常在几十m到几百m之间，故F1、F2的数量级通常在104～105之间。工人上下爬动通常比在地面平动费劲，简单假设为上下爬动1 m等同于在平面走2 m，故第1 个因素（平动）权重为1，第2 个因素（上下爬动）设为2。第4、第5 个因素都是变动次数，F4、F5的数量级通常在几到十几，故需要放大数量级，本文取了1 000，使其在总适应度值中达到合适的比重。第3个因素选取权重思想类似。因素4 中安装每个部件所需要的工人数量和因素5 中安装各部件所需工具可由工程经验指定。

约束条件考虑以下5 条：

（1）立柱要在高空横梁安装之前安装，即2 ～5 排在14 ～16 之前，根据图1，该条可具体简化等效为2、3排在14 之前，4、5 排在15 之前。

（2）试验件需要在支持夹具之后安装好，即11 ～13 排在1 之前。

（3）试验件需要在高空横梁之前安装，即1 排在14 ～16 之前。

（4）高空横梁3 附带作动筒需在高空横梁1、高空横梁2 之后安装，即14、15 排在16 之前。

（5）杠杆系统17 需要在试验件1 之后安装，即1排在17 之前。

对于不满足约束条件的顺序序列，在该序列的适应度函数值的基础上加上一个较大的常数惩罚值，本算法中取200 000。

程序中对适应度函数第5 条安装所需工具的处理：为了方便程序编程，将5 种工具分别与1 ～5 这5个数对应，将这17 个零部件与其自身安装所需工具种类建立17 ×5 的二维矩阵数组，见表2，矩阵（i，j）中1表示安装该零部件i需要工具j，0 则表示不需要。通过相邻两个零部件的五列元素相减就可得出安装前后两个零部件所需的不同安装工具的数量。

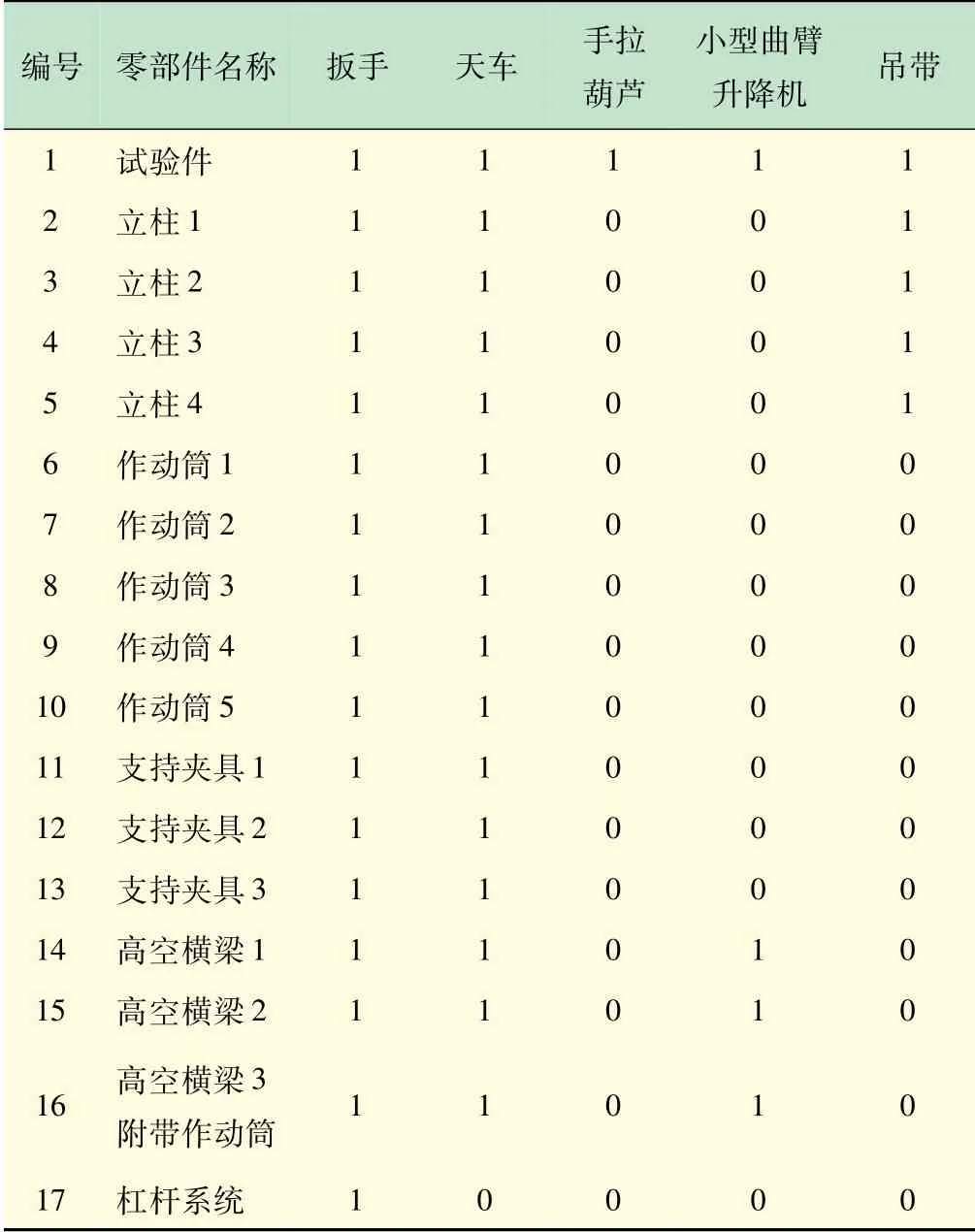
表2 各零部件安装所需工具对应关系

3.3 选择、交叉和变异方法

本算例采用常规的轮盘赌选择法作为选择方法。交叉方法分两步完成。

第1 步选择出需要交叉的2 个个体后，随机产生2 个数i和j（在1 ～17 之间），交换从第i位开始至第j位之间的顺序段，具体过程如图2 所示。图2 中的两行17 位的数字序列分别代表需要交叉的2 个个体，假设随机产生出来的i 和j 分别为12 和15，则交换第12 ～15 位之间的顺序片段。

图2 交叉过程示意图

第2 步对交换后的2 个个体中出现两次同一数字进行排除，保留上述交换的顺序段，替换顺序段之外的相同数。以图2 中交换后第1 个个体为例，数字“2”和“14”出现了两次，同时也意味着该个体有两个数字缺失。保留第1 步中交换顺序片段中的“2”和“14”，缺失的数字包含在第2 个个体中的交换顺序片段中，本例为“17”和“3”，分别以“17”和“3”替换第1个个体中交换顺序片段外的“2”和“14”。第2 个个体操作同上。替换完成后个体不会出现重复数字，且数字遍历了1 ～17，符合个体要求。

变异方法为随机产生2 个数i 和j（在1 ～17 之间），交换从第i位和第j位的数。

3.4 遗传算法运行参数

本算例的部分参数设置为：初始种群数量100，最大迭代步数为300，交叉概率为0.8，变异概率为0.2。由于遗传算法求出的是局部最优解，为了尽可能将得出的解接近最优解，可多次运行该程序，或者增大种群数量，增加迭代次数，从每次的结果中挑选出一种最优解。

3.5 优化结果

本算例共运行了5 次，适应度值集中在75 000 ～83 000 之间，在第2 次运行中得出了最优解。最优解的最小适应度函数值为75 394。遗传算法得到的最优安装顺序为：9-10-8-6-7-11-12-13-3-5-4-2-1-17-14-15-16，解码后安装顺序为作动筒4-作动筒5-作动筒3-作动筒1-作动筒2-支持夹具1-支持夹具2-支持夹具3-立柱2-立柱4-立柱3-立柱1-试验件-杠杆系统-高空横梁1-高空横梁2-高空横梁3 附带作动筒。其中：xz 平面距离和F1＝40 380. 3，权重系数w1＝1，F1w1＝40 380。高度差之和F2＝7 507.0，权重系数w2＝2，F2w2＝15 014。试验件安装过程安全性F3＝4 000，权重系数w3＝1，F3w3＝4 000。装配工人变动次数F4＝7，权重系数w4＝1 000，F4w4＝7 000。安装所需工具变动次数F5＝9，权重系数w5＝1 000，F5w5＝9 000。

最优解的空间示意图如图3 所示，收敛过程如图4 所示。

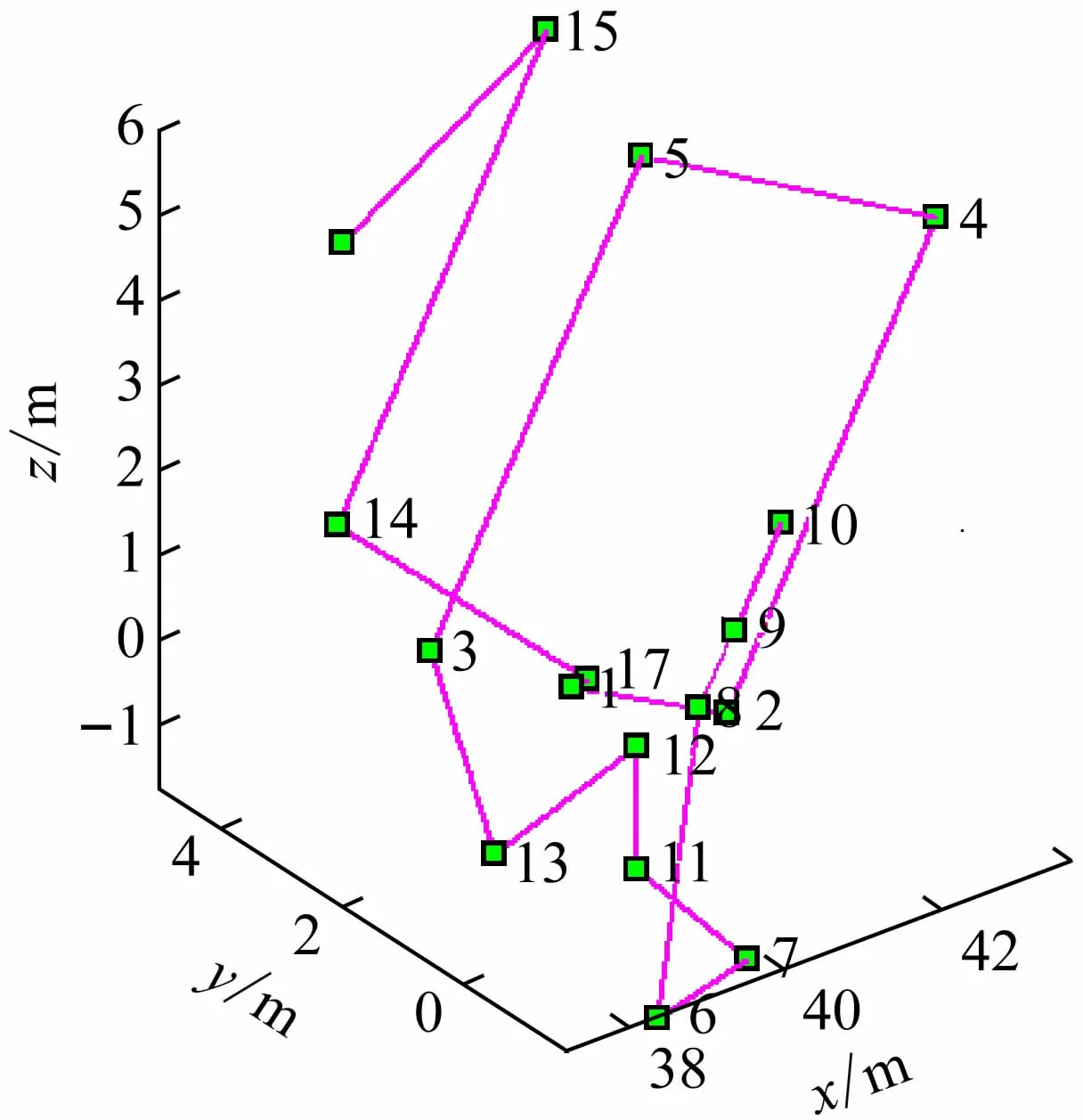
图3 安装顺序空间示意图

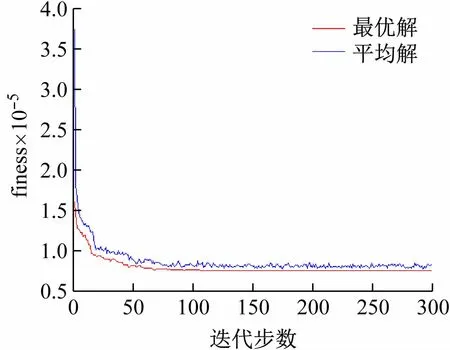
图4 遗传算法迭代步数迭代收敛过程示意图

4 结 语

本文提出的算法可实现结构强度试验安装顺序规划，找出接近或等于最优解的安装顺序。但仍有一些工作可以进一步完善。①约束条件增加得越多，算法出现不满足约束条件的解得概率越大，因此可以考虑基于工程经验，多预设一些安装规则，减少约束条件，节约方案搜索的计算量；②考虑到试验前有大量的加载方案调试工作，也会与安装工作有所耦合，可以把作动筒调试也当作一个安装环节参与排序；③权重系数直接影响适应度函数，本文取的是假定值，实际上应结合真实的试验情况根据工程经验确定权重系数。

本文所提出的模型可进一步完善，读者可以参照本文提出方法更改的适应度函数，针对具体试验特性增加新的影响装配顺序的因素。例如考虑工人的劳动强度问题，合理制定休息时机和时间。安装某些夹具的过程中需要使用叉车，但某些夹具先安装后可能会挡住叉车的行驶路径等。

除了本文提出的方法，也可从另一个思路解决结构试验装配顺序优化，即通过机器学习的方法，不断地对已有大量不同试验的安装顺序进行学习，从而对一种新的试验，能直接给出最优安装顺序。