考虑温度影响的硅钢片磁致伸缩测试实验

刘行谋， 吴佳馨， 王 伟， 张晨阳， 江 帆， 会 燕

（1.重庆邮电大学重庆市复杂系统与仿生控制重点实验室，重庆400065；2.国家电网重庆市綦南供电局，重庆401420；3.国家电网重庆市北碚供电局，重庆400700；4.国家电网重庆市检修分公司，重庆400000）

0 引 言

电力设备的电磁振动主要原因是内部材料的磁致伸缩效应，研究铁磁材料的磁致伸缩特性对分析电力设备运行状况有着重要作用［1-3］。正常运行时电力设备中内部铁磁材料工作在线性区域；然而当电力设备发生故障时，铁磁材料可能工作在非线性饱和区［4-5］，进而导致设备振动异常增大和噪声加剧［6-10］，同时设备运行时必然产生不同的工作温度，磁致伸缩随温度的变化情况直接影响了设备的振动情况。因此应考虑在不同温度下的磁致伸缩现象情况［11］。

本文提出了一种可测量不同温度对硅钢片磁致伸缩影响的实验系统。该系统以螺线管产生恒定磁场，主导内部硅钢片发生磁致伸缩。运用陶瓷发热片和温度调节器对硅钢片加热，通过温度传感器采集了硅钢片温度。以高精度应变电阻片测量硅钢片微小应变特性且拟合磁致伸缩变化曲线。结果发现，硅钢片中磁感应强度为1.68 T时达到饱和状态，此时磁致伸缩率高达10.73 ×10-6。而后随磁场继续增加，磁致伸缩率会因为运动磁畴的数量减少而有所减小。为研究温度对饱和磁致伸缩的影响，对硅钢片进行加温，测量从20 ～80 ℃间磁致伸缩率的变化情况，得出先增加后降低的非线性特性。实验证明了基于磁场、温度和应变传感器的磁致伸缩测量装置的有效性，为电磁设备的设计提供了准确依据。

1 基于螺线管的磁场发生器

1.1 螺线管磁场计算

为得到简易的小范围恒定磁场，本系统采用直流螺线管的方式实现。该方法对磁场大小易于调节，磁场分布波动较小，其结构剖面图如图1 所示。

图1 螺线管设计剖面图

如图1（a）表示单层结构的螺线管，z 轴向为磁场方向，其磁感应强度B0可表示为

当l≫r时，式（1）简化为

式中：I为励磁电流；l为螺线管长度；n1为螺线管单位长度上的匝数；r 为螺线管的半径；z 为螺线管中心O至轴线上某点的距离。

要达到较强磁场，单层螺线管则需要更大电流，因此为节约实验室资源，采用多层螺线管。图1（b）所示的多层螺线管外半径为r1，内半径r0，线圈的厚度为r1-r0。每层单位长度的上匝数为n1，单位厚度上的匝数为n2，可得到轴向磁场强度为

当z ＝0，即螺线管中心点处极小范围内磁场强度为

1.2 螺线管磁场仿真与测试

通过有限元软件模拟并制作计算多层螺线管，其具体参数为：300 mm长的耐温PVC管构成线圈基底，线圈为3 层共330 匝。内径44 mm，外径70 mm，线圈长260 mm。经计算得出螺线管磁场分布仿真如图2所示，可知螺线管内磁通密度分布均匀，场强大小可达到实验要求。

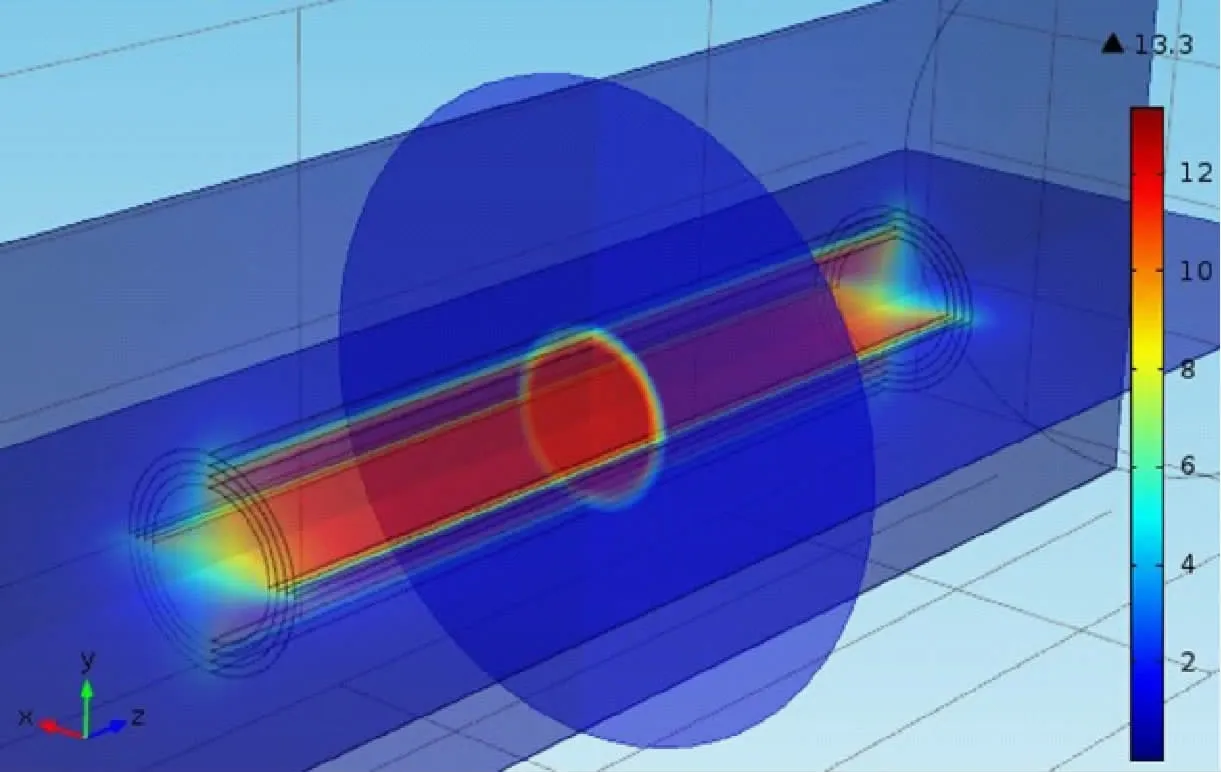
图2 螺线管磁通密度分布仿真

为进一步测试螺线管性能。采用CH-3600 高精度三维磁场测试系统对螺线管内磁场进行测量和标定，其测试实物图如图3 所示。通过霍尔传感器对螺线管内3 个方向的磁场强度测量，将数据采集到DAS系统并由工控机IPC并进行存储。得到的结果拟合后与有限元仿真结果对比，如图4（a）所示。

如图4（a）所示，螺线管中磁场强度实际测量结果与仿真结果在轴线中段高度吻合，仅在管口两端衰减速度不同，这是因为实际螺线管绕制中两端的紧密度难以保证的原因，但不影响硅钢片局部区域内的测量［12］。图4（b）表示了螺线管内中心处磁感应强度随输入直流电流变化的线性变化情况，该结果表现了非常好的线性度。当直流电流为10 A时，管内磁感应强度达到12. 91 mT，该强度已达到对硅钢片测量的要求。

图3 螺线管磁场测定系统

图4 螺线管磁场分布仿真与测试结果比较

2 磁致伸缩测量系统设计

考虑温度的影响设计硅钢片应变测试系统。以30Q120 型取向电工硅钢片为例，其测量系统如图5 所示。选择XH-RJ404020 陶瓷发热片为硅钢片加热，采用PT100 型温敏电阻对温度进行反馈。采用BF120型高精度电阻应变片分别贴于硅钢片中心处。由温控器（TC）调节发发热片功率，以保持特定温度。

图5 硅钢片磁致伸缩测量设计

2.1 硅钢片磁场及温度分布计算

由于硅钢片磁导率相对空气较高，因此实验中可不考虑漏磁的影响。计算本构关系：

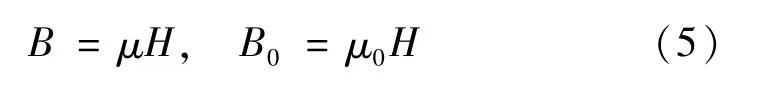
式中：μ为硅钢片磁导率，其曲线如图6 所示；μ0为空气磁导率0.4πμH/m；B0为空气中磁感应强度，则可计算得硅钢片中的磁场分布。

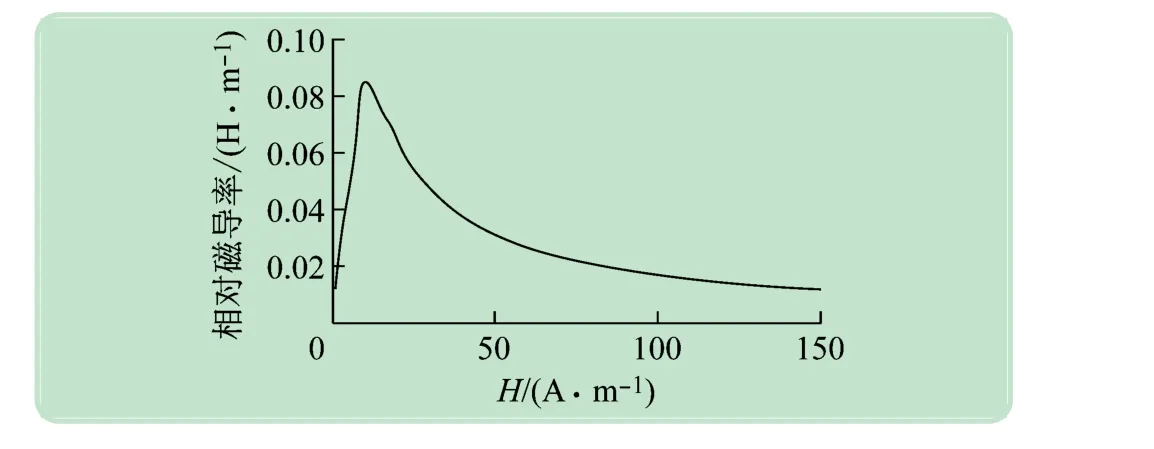
图6 硅钢片磁导率曲线

为保证准确测量在温度影响下的硅钢片特性，要求对测量区域内磁场和温度分布均匀。运用有限元软件对硅钢片在螺线管中的磁场进行模拟。图7 显示了硅钢片在螺线管中沿轧制方向的磁场分布，在硅钢片两端磁场衰减明显，在中间区内磁场分布均匀稳定。

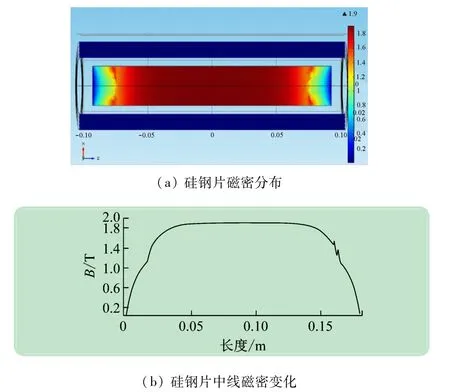
图7 硅钢片磁场仿真分析

用COMSOL软件对陶瓷发热片和硅钢片温度场进行仿真。图8 显示了硅钢片温度分布情况，在硅钢片两端温度下降明显，相对于磁场，均匀温度分布的区域明显减小。但在中心处测试区的小范围内磁场和温度均完全满足试验要求，可用于对硅钢片测试。

2.2 硅钢片应变测量

本文采用一种非电量的电测方法，以BF120 型应变电阻作传感器的非平衡电桥法来测量磁致伸缩系数

式中：C 为恒定值，由测量电路和应变传感器参数确定。故只需测出流过电桥的电流Ig即可得出磁致伸缩系数λ。建立不同的外磁场H，可计算出各种外磁场强度下的λ，然后以H作为横坐标，λ作为纵坐标，画出一条磁致伸缩系数随外磁场强度变化的曲线，根据曲线求得λ ＝f（H）的经验公式［13-15］。

图8 硅钢片温度仿真分析

3 实验测量及结果分析

实验传感器安置如图9 所示。将Hightemperature Co-fired Ceramics（MCH）作为热源用高导热硅胶粘于硅钢片底部中心位置。实验中需设置同样布置的硅钢片作为对照组安置在室温环境下，以平衡测量电桥的参数和消除误差。实验过程中调节直流电流大小和发热片功率，测量并记录硅钢片应变值。

图9 实验装置及测量过程

保持室温20 ℃，调节螺线管的直流电流，使其螺线管内磁感应强度从0 变化到2 T。在该过程中对硅钢片二维方向上的应变量进行读取和记录。将测量结果通过三次样条插值拟合为单值曲线，其结果如图10所示。从图中可知，硅钢片在轧制方向上的最大值达到10.73 ×10-6，此时磁感应强度为1.68 T。当磁感应强度大于1.68 T时，硅钢片在该方向上的磁感应强度规律与前者一致，但最大应变量约4.29 ×10-6。这现象表明了取向性硅钢在磁化过程中具有方向性，轧制方向是磁化效率最高的方向。

图10 磁致伸缩测量拟合曲线

通过对硅钢片温度的采集和发热片功率的调节，可实现不同硅钢片温度下的最大应变测量。将温度设置在20 ～80 ℃时，测量得到硅钢片磁致伸缩如表1 所示。同样从结果中可发现，在不同温度下轧制方向上的应变量始终是最大的。将数据结果拟合为曲线，如图11 所示。

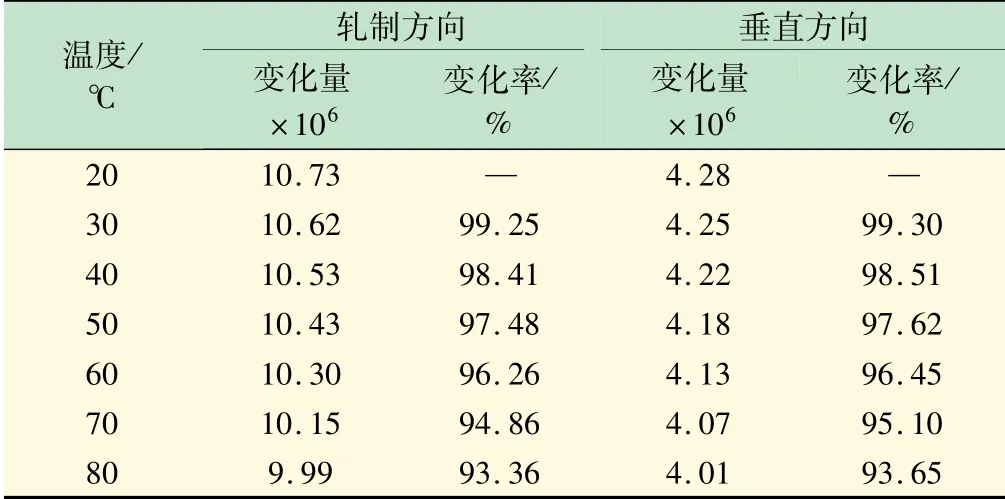
表1 磁致伸缩随温度变化率

图11 硅钢片磁致伸缩随温度变化测量结果

结果表明，磁致伸缩峰值具有十分明显的非线性特性。当温度升高越快，磁致伸缩变化率却越小。温度为80 ℃时，硅钢片轧制方向上的磁致伸缩率下降到室温的93.36%，其垂直方向上的磁致伸缩率下降到室温的93.65%。虽然磁致伸缩随温度的变化并不明显，但在大型电磁设备中微小的应变量仍然不能忽视。

4 结 语

本文基于应变传感器和温度传感器设计了一种考虑温度影响的硅钢片磁致伸缩测量的装置。从理论和仿真上分析了该设计的可行性。搭建该实验平台对硅钢片进行了实测，测量结果表明硅钢片的磁致伸缩变化与磁化过程具有同样的规律特性，它们都随着外磁场的增加，逐渐达到饱和，而饱和后磁致伸缩率后适应降低。此时，硅钢片磁致伸缩率还随温度增大而呈现非线性增大关系。结果表明，随温度的增加磁致伸缩呈现降低趋势，并温度越高降低越快。证明了该测量系统可对铁磁材料磁致伸缩进行准确测量。