基于均值漂移聚类的端元束提取

陈立伟，邱艳芳，朱海峰，王立国

哈尔滨工程大学 信息与通信工程学院，黑龙江 哈尔滨 150001

由于空间分辨率的限制以及地物分布的复杂多样性，混合像元普遍存在于高光谱遥感图像中。因此，实际应用中必须解决光谱解混的问题。光谱解混主要分为端元提取和丰度反演2个步骤。近年来，有多种端元提取方法相继提出，最具有代表性的为像元纯度指数算法(pixel purity index，PPI)[1]，内部最大体积算法 (N-FINDR)[2]，单形体增长算法(the simplex growing algorithm，SGA)[3]，和顶点成分分析(vertex component analysis，VCA）[4]等。这些端元提取方法只能从高光谱数据中提取单一端元代表一类地物。由于光照辐射条件的变化、时空等自然因素变化的不可测影响，高光谱遥感图像中地物普遍存在光谱变异性[5]。此时，单一端元对地物类别的代表性有限，影响对真实地物丰度反演的精度。因此，从高光谱遥感图像中为每一种地物类别提取多个代表端元，并形成端元束（endmember bundle，EB）[6-7]，是处理光谱变异性的一种简单有效方法。

端元束提取分为2个步骤：获取候选端元，对候选端元进行聚类。聚类的目的是形成每种地物的代表性端元光谱集合。在聚类阶段，目前常用的算法就是K 均值（K-means）聚类[8]，K-means算法对于大型的数据计算简单高效，且时间和空间复杂度都较低，在高光谱图像分类中也有应用[9-10]。但是K均值聚类算法需要预先知道类簇的数目，在光谱聚类中表现为需要预先知道高光谱遥感图像中地物的类别数目。但是地物类别数目的估计通常是很困难的[11]。地物类别数目的估计误差会对聚类结果产生直接的影响，从而增加多端元光谱混合分析的计算量[12]。

1 候选端元提取

端元提取的方法有很多，大致可以分为基于几何学和基于统计学的算法。这些算法中大多数都是利用光谱的信息进行端元提取，而目前已有研究者对空间信息加以利用，与光谱信息结合提取图像中的端元，将此类方法运用于端元束提取的潜力已经被证明[13]，因此文中候选端元的提取采取空间信息和光谱信息相结合的方法[13]，主要分为3个步骤。

1）PPI（pixel purity index）预处理。运用 PPI算法对候选端元进行粗略的筛选，此处阈值T设置为0，生成随机向量的数目设置为K（地物种类数目为10～15时，K设置为10 000）。经过PPI算法的计算会提取出大量的候选端元，此步骤也是为了减少下一步骤的计算量和复杂程度。

2）同质性指数（homogeneity index，HI）的计算。文献[14-15]中指出，端元一般位于空间同质区域内，混合像元一般位于过渡区域或者不均匀的区域。在此基础上，文献[16]将相邻像素的相似度定义为HI，通过对像素点与邻域内其他像素的光谱信息散度（spectral information divergence，SID）来定量测量HI。HI值越小，像素点为纯像元的概率越大。

3）基于区域的端元选择。在该步骤中，根据HI的阈值来选择端元。在不同的环境，对于不同的材料，端元的光谱变异程度不同。为此，对整个图像进行分块，自适应地为不同的块选择不同的阈值，从不同块中获得端元集合，其中初始阈值由HI值的统计直方图确定。根据选候端元的比例自适应地调整该阈值，图像块的大小是依据图像的复杂程度来划分的。如果地物分布广泛且均匀，则块的尺寸可以稍大[17]，反之亦然。

2 基于均值漂移聚类的端元束提取

2.1 均值漂移聚类

均值漂移（mean shift）算法是一种无参密度估计算法或称核密度估计算法[18]，在聚类、图像分割、跟踪等方面有着广泛的应用。Mean shift是一个向量，它的方向指向当前点上概率密度梯度的方向。在聚类中，该算法完全依靠特征空间中的样本点进行分析，不需要任何先验知识，数据集中的每一点都可以作为初始点，它能对任何维度、任何分布的采样点进行快速聚类，迭代效率高。

均值漂移指的就是聚类中心根据偏移向量的均值进行移动，偏移均值为式中：Sh指的是以数据x为中心，半径为h的圆形区域；k是指区域Sh内所包含数据点的个数；xi是指圆形区域范围内的第i个数据点。的方向就是聚类中心移动的方向，聚类中心的移动距离就是的模。

某一时刻聚类中心的计算为

式中：Mt是指在t状态下的偏移均值；xt、xt+1分别指的是状态t和t+1时的聚类中心。

2.2 基于光谱角距离准则的均值漂移聚类

传统的均值漂移聚类算法通常使用欧氏距离作为聚类的判决准则，同一地物的变异光谱在空间中的位置比较靠近，但是当变异较大时，变异端元的位置也可能距离较远，传统的均值漂移算法就不再适用。同一物质的变异光谱之间在多维空间中的光谱角较小，故本文在均值漂移算法采用光谱角距离（spectral angle distance，SAD）作为聚类的判决准则。2条光谱 xa和 xb之间的SAD计算为

2）标记以该中心光谱为中心，光谱角距离为半径，半径为h的圆形范围内所有的光谱数据，记做集合，将这些点划分为一个簇。同时，记这些光谱的标记次数为1。

6）重复步骤1）～5）直到所有的样本都被标记访问。根据每个类，对每个样本的访问频率，取访问频率最大的那个类，作为当前点集的所属类。

均值漂移聚类方法不需要预先知道地物的种类数目，完全依靠现有的光谱数据进行分析，尽可能避免由预估地物类别数目算法带来的误差，更准确地形成端元束。下面通过实验对改进前后的均值漂移聚类方法以及K均值聚类算法在端元束聚类方面进行了比较。

3 实验结果与讨论

3.1 模拟数据实验

3.1.1 变异光谱的合成

要合成混合高光谱图像，首先需要合成变异光谱。本文从USGS光谱库中选取4种地物光谱作为原始光谱，如表1所示。考虑光照引起的变化，本文基于端元扰动理论去合成光谱[19]。文中将各地物光谱的变异系数分别为设置为：0.1、0.35、0.25和0.25；使用的USGS光谱库中光谱波长在380～2 500 nm，共224个波段，合成后光谱如图1所示。

表1 选择的地物名称

图1 合成的变异光谱

3.1.2 混合高光谱图像的合成

实验中使用的是大小为1 2 8×128×224，由上述变异光谱线性混合而成的图像，并在图像中加入40 dB的高斯白噪声。合成的混合高光谱图像中存在纯像元，将变异光谱和原始光谱均视为端元，序号为1～3的端元丰度大小均以各自圆心向外发散，圆心在高光谱图像中的位置分别为[50,30]、[100,64]以及[50,100]，在距离圆心越远位置的混合像元中，该端元所占的比例越小。序号为4的端元则与之相反，丰度分布情况如图2。

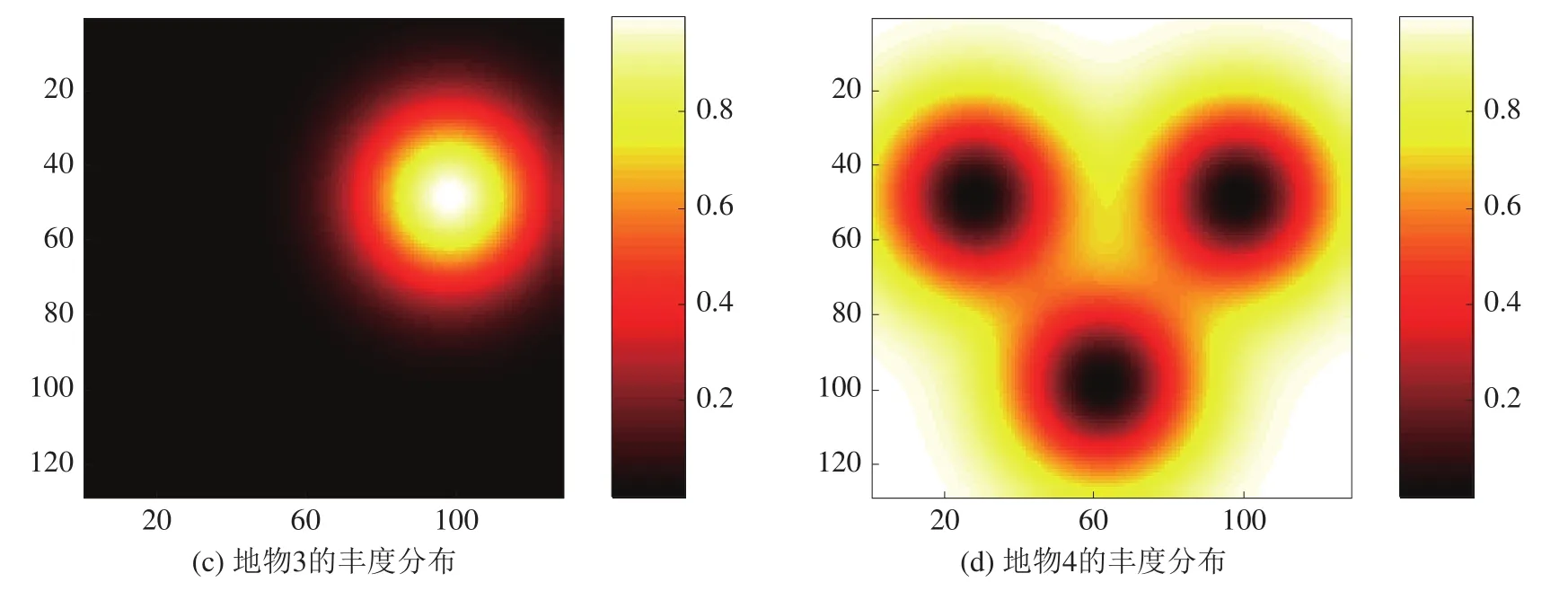
图2 丰度分布

3.1.3 实验结果及分析

在端元集提取部分，有几点需要指出：1）PPI预处理算法中的阈值设置为T=0，可以确保提取到的光谱中包含了所有的4类地物；2）PPI预处理只是做一个粗略的筛选，其中随机向量的数量远远小于传统PPI算法中随机向量的数量，本次实验中将K设置为50 000；3）在实验中，根据HI直方图将数据块的大小设置为20×20，并将阈值设置为0.013（如图3所示）。

在光谱聚类部分，1）由于混合图像中选取了4类地物，故K-means聚类算法中聚类中心的个数设置为4；2）均值漂移聚类算法中的半径设置为0.9，中心点移动距离误差设置为0.14，与聚类中心之间的欧氏距离误差设置为0.2；3）改进后均值漂移聚类算法中的半径设置为2.26，中心点移动距离误差设置为0.14，与聚类中心之间的欧氏距离误差设置为0.16；4）聚类后的光谱束与USGS光谱库中的光谱进行对比，选择光谱角距离最小的地物作为光谱束所代表的地物类别。

图3 合成数据的HI直方图

按照改进后的均值漂移算法进行聚类，其结果如图4所示，图中依次为Actinolite、Brucite、Corundum以及Goethite。

图4 改进后的均值漂移聚类结果

本文将通过光谱类内部的分散程度和光谱类之间的分散程度来度量聚类性能的优劣。光谱类内部分散程度越小且光谱类之间的分散程度越大则聚类效果越好。实验中以各类光谱中光谱的平均值作为类中心光谱，光谱内部分散程度采用的是类内各光谱到类中心光谱的SAD值来表示，光谱类间的分散程度采用的是各类的中心光谱之间的SAD来度量，SAD值越小说明越聚集。因为一组光谱代表的是一类地物，所以每一类地物都会有相应的一组类内SAD值以及类间SAD值。

分别使用K-means和未改进的meanshift的算法进行对比，每组类内SAD值的统计信息结果如图5所示，其中的数字表示的是该类光谱束中的所拥有的光谱的数目。

各类光谱束的中心光谱间的SAD值如表2所示。序号所对应的端元与表1中一致。

图5 地物类内SAD值的统计信息

表2 各类的中心光谱间的SAD

实验结果表明，在未知端元数目的情况下，均值聚类算法也能聚类出正确类别数目的地物；由图5可以看出，Brucite使用3种方法的聚类效果完全相同；Corundum使用改进后的均值漂移算法时的最大观测点较小，离群点较少，整体数据比较集中；Actinolite使用改进后的均值漂移算法聚类式的箱图更加的矮胖，数据集中效果更好。Goethite光谱束中，改进后的meanshift聚类较K-means聚类箱图更加矮胖，数据整体比较集中；较未改进的meanshift算法整体观测点更小，表明光谱束之间的光谱角更小。表2中显示了各类中心光谱之间的SAD值，使用K均值算法时，Actinolite与Goethite、Corundum与Goethite之间中心光谱的SAD值都较小，分别为0.177 5和0.087 6，类间的分离程度不高；改进后的均值漂移算法整体上的类间SAD值略高于K均值算法以及传统均值漂移算法，类与类之间的差异性更大，分离程度更高。

3.2 真实数据实验

为了评估均值漂移聚类算法在不同的分析场景中的有效性，接下来用真实图像进行实验。实验所采用的覆盖Cuprite场景的真实数据集于1997年被机载可见红外成像光谱仪（AVIRIS）传感器捕获。Cuprite原始数据有224个波段，范围覆盖370～2 480 nm。此处选择了Cuprite数据中的50个波段，大小为190×250的数据。由于USGS光谱库有大量的可用于现场地面真实数据，该数据集已成为用于算法评估的常用基准数据集。Swayze和Clark[20]也制作了一份关于该地区基本事实的报告。端元集提取部分需要指出的是：1）实验中的PPI预处理算法将阈值设置为0，生成的随机向量个数为12 000；2）Cuprite数据的HI直方图如图6所示，由图6将数据块的大小设置为20×20，并将阈值设置为0.014；3）在聚类部分，地物类别的数目为12[20]，故K-means聚类算法中中心点个数设置为12；均值漂移聚类算法的半径设置为5；中心点移动距离误差设置为3.2；聚类距离误差设置为13；以上数值在改进后的均值漂移聚类算法中分别设置为 0.03、0.002、0.037。

通过2种均值漂移算法聚类之后均可得到11种地物类型，如图7和8所示。

图6 真实图像数据的HI直方图

图7 均值漂移聚类结果

图8 改进后的均值漂移聚类结果

K-means算法聚类之后共得到12个光谱束，将这些光谱束与USGS光谱库中的地物光谱进行对比，同样得到11种地物，其中与改进后的均值漂移算法所得的地物类型相同的地物有7种，如图9所示，依次为：Oligoclase HS110.3B、Mizzonite HS350.3B HLSep、 Lazurite HS418.3B、Desert_Varnish ANP90-14、 Mizzonite NMNH113775-1、Kaolin/Smect KLF506 95%K、Montmorillonite CM26。

根据结果图7可明显看出，在未经改进的meanshift算法聚类中，有明显的聚类错误情况出现，聚类效果不如K-means算法以及改进后的meanshift算法，因此接下来只将K-means以及改进后的meanshift算法进行比较。将2种算法所得的这7种相同类型的地物的SAD统计信息进行比较，各端元束内部的SAD信息如图10所示（除去类内只有一条光谱的地物，Mizzonite NMNH 113775-1和 Montmorillonite CM26）；各类光谱束的中心光谱间的SAD的信息如图11所示。

图9 K-means聚类结果

由图10可以看出，对meanshift算法进行改进后，聚类结果中所有地物均无离散点的出现，整体而言，聚合程度较好；其中Desert_Varnish ANP90-14的类内SAD值在最大值、最小值以及中值等方面小于K-means算法，具有明显更优的聚类效果；Oligoclase HS110.3B和Lazurite HS418.3B 2种地物的聚类情况略逊于K-means算法。由图11可以看出，2种算法得出的各个端元束的中心光谱之间SAD值的分布情况大致相同，在预先未知地物种类的情况下，改进后的均值漂移算法所得到的结果较K-means算法无明显缺点存在。

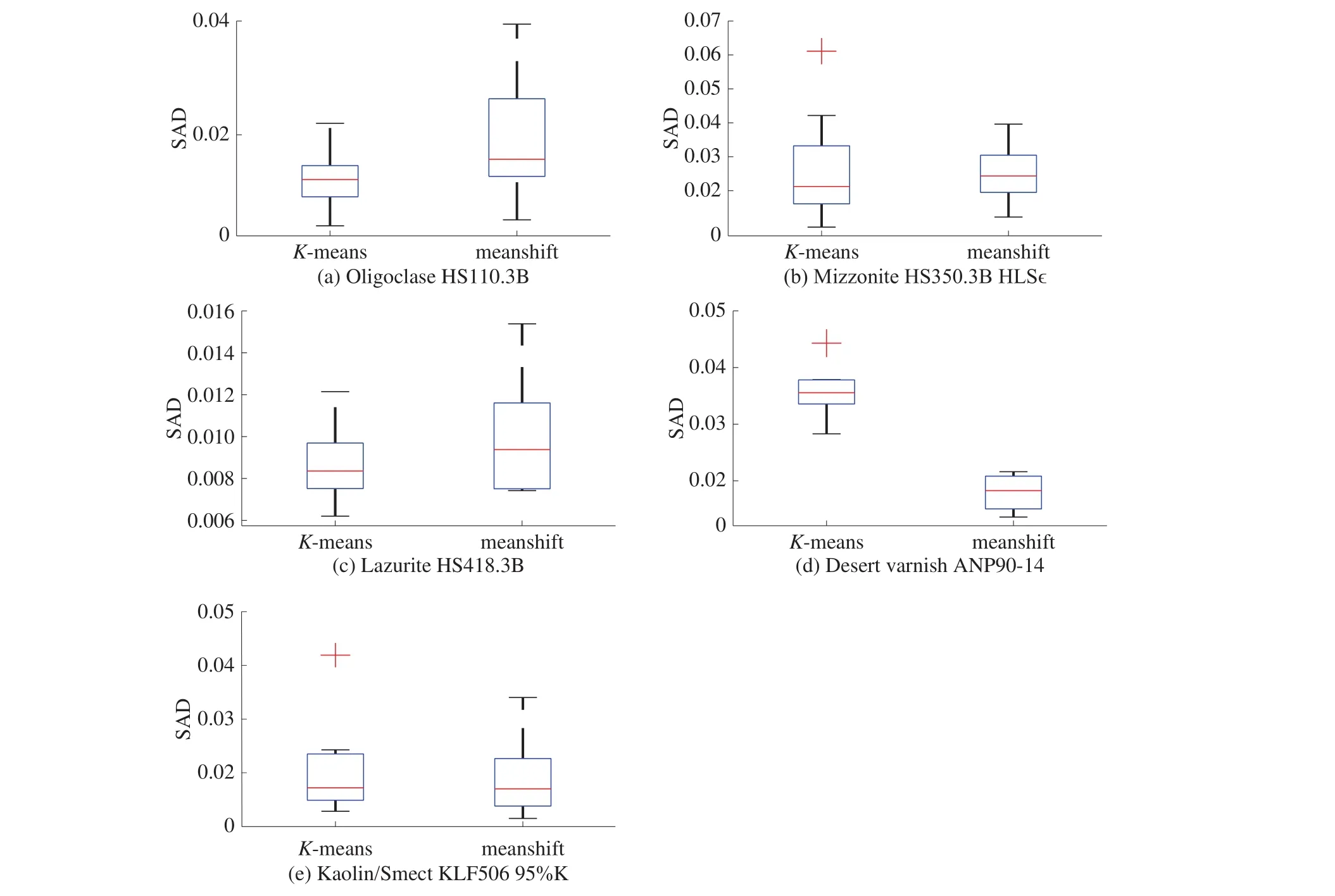
图10 2种聚类方法的5种相同地物的类内SAD统计信息

图11 各类的中心光谱间的SAD统计信息

4 结论

端元束提取中的聚类影响多端元光谱混合分析的效率。本文对传统的均值漂移聚类算法进行改进，将改进后的方法应用于光谱聚类中，并将其结果与K-means聚类方法以及传统的均值漂移算法结果进行比较。

1)在不需要预先知道地物种类数的前提条件下，均值漂移聚类算法能够依靠数据自身的特点对数据进行聚类。

2)通过模拟数据和真实数据实验的验证，基于光谱角距离的均值漂移算法较原方法更加适合光谱聚类，且在整体效果上较K-means算法有一定的优势，聚类后的数据集类内的离散程度更低，类之间的分离程度更高。

端元束的有效聚类，有利于提高多端元光谱混合分析的效率，对于高光谱遥感定量解译具有重要意义。