大口径舰炮摇架的结构优化

富威，吴琼，龚军军，赵书樊，左沅昊

哈尔滨工程大学 机电工程学院，黑龙江 哈尔滨 150001

在火炮研究方面，张新建[1]建立了火炮上架结构在3种典型射角工况下的有限元模型，利用层次分析法得到各子工况下基于柔度的权重组合系数。李志旭[2]利用神经网络法建立了误差变量、优化变量和优化目标函数之间的数学模型，采用双层嵌套的优化求解方法，以质量和炮口扰动为目标，针对摇架结构尺寸进行了不确定性优化，考虑其弹性模量、密度、泊松比等材料特性参数误差。萧辉[3]提出了一种基于自适应径向基函数(RBF)神经网络的结构优化方法。周乐[4]利用ADAMS底层开发模块，结合小生境遗传算法程序建立多目标优化函数，进行火炮反后坐装置结构多目标优化设计。王明真[5]使用isight软件，针对某火炮结构轻量化的问题，研究了两种火炮大架的结构，并完成了火炮大架形状和尺寸的优化。孙明颜[6]对某种摇架结构进行了有限元分析，并在这个基础上，使用变密度法针对摇架进行了以体积最小为目标的拓扑优化，得到了一种新的摇架结构。岳炯等[7]采用有限元方法对舰炮的结构进行了模态分析，基于响应面法构建了响应面近似模型，同时利用变密度法针对舰炮的结构进行了结构优化。蔡文勇[8]首先对火炮系统进行了动力学分析，同时基于遗传算法针对火炮架体的总体结构进行了优化，得到了一种优化模型。杜春江[9]采用APDL语言分别编写了两种优化程序，并将其应用到了某车载火炮的驾驶室内结构优化的设计。边海关[10]提出了针对拓扑优化结果改进的上架设计方案，并进行有限元分析，通过对优化前后的上架最大位移对比，优化后最大位移和质量均比之前有所减小，优化后的上架刚度有所提高，使得火炮发射时两耳轴中心变位差有所减小，对提高火炮的射击密集度起到一定的作用。范林盛[11]通过选取某火炮摇架承载最恶劣的2个工况，根据摇架的受力情况，基于Hypermesh-Opti Struct软件平台建立其有限元模型，采用变密度方法的拓扑优化技术，对摇架进行拓扑优化。张鑫磊[12]建立了基于非线性有限元理论的全炮刚柔耦合动力学有限元模型，计算分析得到了摇架的动态响应。朱家萱[13]基于火炮摇架结构本身特点和承载特性，在力学分析基础上利用有限元法针对火炮后坐过程中的摇架动态响应进行了仿真计算和数值模拟，并通过拓扑优化方法和设计理论针对摇架结构进行了优化设计。目前，结构优化设计已经应用在解决机械、建筑等各种实际工程问题，能够很好地对结构进行轻量化，提高结构的性能和使用寿命等[14]。国外，Bennage等[15]针对单目标和多目标结构优化问题，提出了一种基于Monte-Carlo方法的多变量优化方法，这个过程被称为模拟退火，它将物理系统中的能量最小化与结构系统中的目标函数最小化进行了类比；Nikolaos等[16]研究了各种进化算法在应用于大规模结构尺寸优化问题时的效率，如遗传算法和进化策略；Sobieszczanski等[17]针对飞机等大型工程结构设计中设计变量比较庞大的问题，提出了一种将大型多学科混合优化问题分解为若干小子问题的方法；Krister等[18]提出了一种使用非线性规划来进行结构优化的方法；Amir等[19]提出了一种新的优化算法布谷鸟搜索，用于求解结构优化等问题。

在国内，结构优化的发展也比较好，1995年，顾元宪等[20]编写了MCADS软件，该软件满足工程设计中的实际应用，具有强大的功能和易操作性；叶元烈等[21]对薄壁覆盖件进行分析，选择了SQP方法对对其进行优化，并编写了OPTSHEET程序；黄康等[22]将有限元方法与人工神经网络相结合，利用人工神经网络的非线性映射能力，可以获得在输入不同参数时能够预测信息的人工神经网络，从而可以很容易地将其转换为优化设计程序；王春会[23]对多工况下的连续体结构进行了拓扑优化设计，分析了影响拓扑优化的几种因素，并且用有限元软件进行验证；罗震等[24]建立了连续体结构拓扑优化的数学模型，并提出了一种可以有效地消除拓扑优化时产生棋盘格的新方案。

1 密度法数学模型

变密度法人为假定单元的密度和材料物理属性之间的某种对应关系，以连续变量的密度函数形式显式地表达这种对应关系，变密度法基于各向同性材料，以每个单元的相对密度作为设计变量，每个单元有唯一的设计变量。变密度法的基本思想是设想出一种密度能够改变、性能参数也可以人为的改变的假想材料，并将它引入到需要优化的结构中，将连续体离散为有限元模型后，将每个单元指定为介于0和1之间的相同密度。在优化的过程中，我们将可变的材料密度作为设计变量，巧妙的将优化问题转变成了关于材料分布最优的问题。通过变密度法建立的数学模型为

式中：W为体积力；η为密度最小值；ρm为单胞密度；x为设计变量；Zi为外部条件；Mo为去掉材料的总质量；Mmax为质量最大值；F1,F2，…，Fn为在优化之后密度固定不变的单元编号。

2 摇架结构的拓扑优化

2.1 摇架优化的模型建立

1)设定优化区域和非优化区域

在Topology Optimization模块下指定模型中的优化区域和非优化区域，对于摇架上的高低齿弧，此处无法进行优化，所以不做考虑。具体情况如图1所示，其中，紫色区域代表想要优化的设计区域，红色区域代表非设计区域。

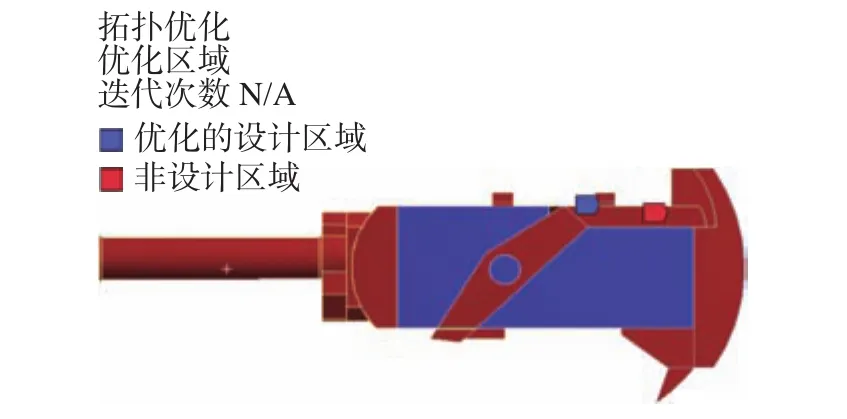
图1 优化的设计区域和非设计区域

2)响应约束

以静力学分析为基础的拓扑优化，在Response Constraint中设置响应约束的时候，类型主要有质量（默认50%）、体积（默认50%）、位移、全局应力（global von-mises stress constraint）、局部应力（local von-mises stress constraint）等选项。首先选择质量约束来进行分析。

2.2 拓扑优化结果

为了使拓扑优化结果更具有说服力，笔者设置了不同的优化目标并进行3次拓扑优化。图2中优化目标是使摇架质量剩余30%，经过18次迭代优化得到的材料分布云图，红色边缘线围成的部分表示区域密度在0～0.4之间，需要去除；棕色部分表示区域密度在0.4～0.6之间，表示边缘，可以去除也可以保留；灰色的部分表示区域密度在0.6～1之间，表示需要保留的地方。为了更能清楚的观察到优化区域的拓扑结构，隐藏了非优化区域的结构。

图2 第1次优化的材料分布云图

在进行摇架的第2次拓扑优化时，将优化目标设置为使第1次优化后得到的新摇架的质量剩余30%，并且最大的制造尺寸为40 mm，经过64次迭代优化得到的材料分布云图如图3所示。

图3 第2次优化的材料分布云图

第3次优化的优化目标为使第2次优化后得到的新摇架的质量剩余25%，并且最小的制造尺寸为20 mm，经过30次迭代优化得到的材料分布云图如图4所示。

图4 第3次优化的材料分布云图

经过3次的拓扑优化得到的摇架结构都是不规则的，但是外形大致相同，都是将一整块板分成上下两个部分，在上下两块板中有一块板有一个类似三角形状的孔洞，并且有一块板中间出现了前后不一样宽的情况，总结可以得到摇架的初步结构模型。因为不规则的形状结构，在实际中加工出来是不可能实现的，所以根据拓扑优化出来的形状进行进一步绘制出一个规则的易加工的模型结构，如图5所示。

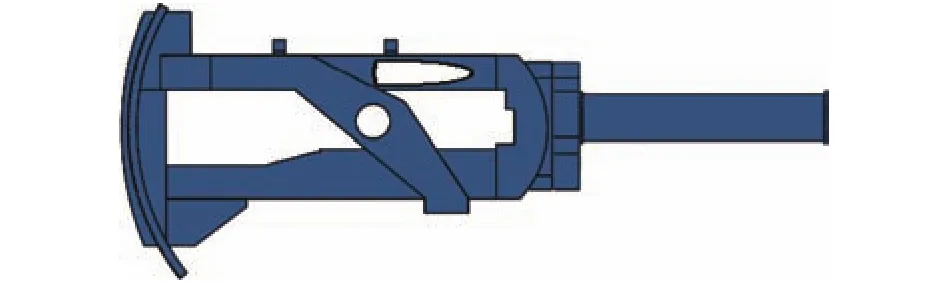
图5 摇架优化结果验证

3 摇架结构尺寸优化

拓扑优化只能设计出摇架结构的大致形状，其最终得到的优化结构是在设定的约束条件和想要达到的目标共同作用下的大致结构。初步得到的摇架拓扑结构为以后摇架结构设计提供初步的设计草图，然后再进一步进行尺寸优化，得到一个摇架的最优结构。

3.1 摇架尺寸优化模型建立

根据之前得到的摇架拓扑结构，重新进行参数化建模。为了保证摇架和其他舰炮典型部位(身管、托架等)的安装尺寸不改变，进行尺寸优化时，只选取宽度尺寸为设计变量。如图6所示，主要选取了摇架的上板宽d1，下板前段宽d2，下板后段与前段的宽度差d3，且d1+d2应该小于右侧边的尺寸，即d1+d2＜1 100 mm，同时，实际的模型结构应符合机械设计方法，应满足上面板的宽度小于下面板的宽度，即d1＜d2。

图6 摇架尺寸优化设计变量

尺寸优化具体分为4个步骤：

1)选取摇架的应力为约束条件，即在舰炮发射时，摇架所受最大应力的部位应小于材料的极限应力值，选取摇架的质量为优化目标，即摇架质量最小，建立摇架尺寸优化的数学模型为

2)根据建立的摇架的优化数学模型，选择遗传算法进行尺寸优化；

3)摇架结构在得到每一组解后，都会进行验证，验证优化结果的合理性，找到满足条件的最优解输出，一共得到了58组最优解集；

4)在摇架结构尺寸优化得到的58组最优解集中，给定了3组最合理的解，对这3组最优解进行验证，选择振动最小的一组，即为所得到的摇架最优结构的尺寸。

3.2 优化的结果

最终得到的尺寸优化结果如图7所示，图7中，点划线代表d3长度的下梁2个不同宽度差，虚线代表d1长度的上梁，实线代表d2长度的下梁。

图7 摇架尺寸优化结果

在这58组数中，得到3组最优解，每组结果对应的尺寸、应力值和质量如表1所示。

表1 摇架尺寸优化最优解

从表1中可以看出，3组优化的数据都在一定的数值附近稳定，为了选出最优的一组解，将新得到的模型进行瞬态分析，位移最小的一组，即为摇架结构的最优参数。按照表1中的3组参数重新建模，进行瞬态分析，分析优化前后摇架的振动特性，判断优化后的摇架模型的振动是否有所减小。瞬态分析的设置和之前的相同，以摇架位移为例，得到的结果如图8所示。

图8 摇架尺寸优化后瞬态分析

从图8中可以看出，优化后方案3中大口径舰炮发射时摇架上某点y方向的最大位移数值最小，为0.994 99 mm，相比原始摇架模型的位移减小了0.350 21 mm，其他方向同理，所以选择方案3为摇架部件的最终结构。从瞬态分析得到的一组最优解的方案中，摇架的最大等效应力为107.57 MPa，质量为5 876.7 kg，相比拓扑优化前得到的摇架的最大等效应力和质量，摇架的最大等效应力变化不明显，在材料的屈服强度以下，符合强度要求，能够满足摇架的使用要求。尺寸优化前摇架的质量为6 059.3 kg，尺寸优化后，摇架的质量减小了3.014%，能够在满足摇架使用技术要求的基础上达到对摇架轻量化的目的，节约了制造材料。

4 结论

1)本文使用ANSYS/Workbench软件进行了拓扑优化和尺寸优化。为了确保结果的正确性，设置了不同的优化目标进行了3次拓扑优化，第1次拓扑优化的优化目标是使摇架结构的质量剩余30%，经过18此迭代后得到了最优结果；第2次拓扑优化的优化目标是使摇架结构的质量剩余30%，迭代了64次得到最优结果；第3次拓扑优化的优化目标为使摇架结构的质量剩余百分之25%，摇架的第3次优化一共迭代了30次得到最优结果。

2)经过3次的拓扑优化得到的摇架结构都是不规则的，但是外形大致相同，都是将一整块板分成上下两个部分，在上下两块板中有一块板有一个类似三角形状的孔洞，并且有一块板中间出现了前后不一样宽的情况，总结可以得到摇架的初步结构模型。

3)为了满足摇架的安装尺寸，选择宽度为尺寸优化的设计目标，确定了摇架后架中的3个主要设计参数；利用遗传算法对摇架进行尺寸优化，求得摇架的3个设计参数的最优解集。并通过瞬态分析，计算大口径舰炮发射时摇架的最大位移，确定了最优的一组解，得到摇架的最终结构。为今后舰炮武器系统设计提供了参考依据。