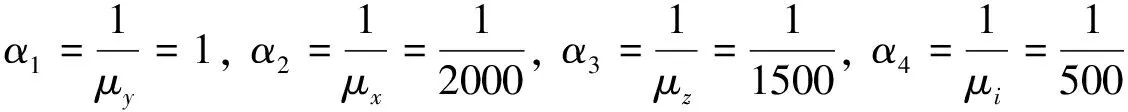稀疏过程下带有退保和分红策略的相依风险模型
(广西民族师范学院 数学与计算机科学学院,崇左,532200)
1 引言
在经典风险模型[1-2]中总假设保险公司在单位时间内收到的保费是固定不变的,发生索赔的次数{N(t),t≥0}服从齐次Poisson过程,索赔额是非负独立同分布的随机变量.基于此,文献[3-7]对其进行推广,考虑随机保费收入、退保因素、分红、利率等干扰因素的影响,建立相应的风险模型,得到了相关的性质、破产概率的上界与最终破产概率等结论.在这些模型中都假设保费到达数{M(t),t≥0}与索赔发生次数{N(t),t≥0}相互独立,但在实际问题中,这两者通常是相依的,收到的保单数越多,发生索赔的次数就会越多.因此文献[8-10]讨论了理赔次数{N(t),t≥0}是保单到达数{M(t),t≥0}的p-稀疏过程,运用破产论的方法讨论模型盈余过程相关函数的性质,给出了最终破产概率的表达式和Lundberg上界.本文在文献[7,10]的基础上引入干扰因素,假设索赔次数{N1(t),t≥0},退保次数{N2(t),t≥0}和支付红利的保单数{N3(t),t≥0}分别是保单到达数{M(t),t≥0}的p1,p2,p3-稀疏过程,建立带有退保和分红策略的相依风险模型,并运用鞅方法讨论该模型盈余过程的性质,给出最终破产概率的表达式和破产概率的Lundberg上界.
2 模型的建立
本文考虑如下风险模型:保险公司在t≥0时刻的盈余
(1)
其中:u为保险公司的初始资本;{M(t),t≥0}和{Ni(t),t≥0}(i=1,2,3)分别表示在时间区间(t-1,t]内保险公司收到的保单数、发生的理赔次数、退保的保单数和支付红利的保单数;Xk表示第k次的索赔额;Yk表示第k张保单收取的保费;Zk表示第k张退保保单的给付额;Ik表示第k次支付的红利额,且当盈余大于或等于给定的非负整数红利界时,保险公司才支付红利;σ表示干扰系数;W(t)是标准的布朗运动,代表公司不确定的收益或损失.本文假设保险公司收取保费、进行赔付、退保及支付红利均在时间区间(t-1,t]的始端进行.
对上述模型(1),做如下假设:
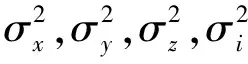
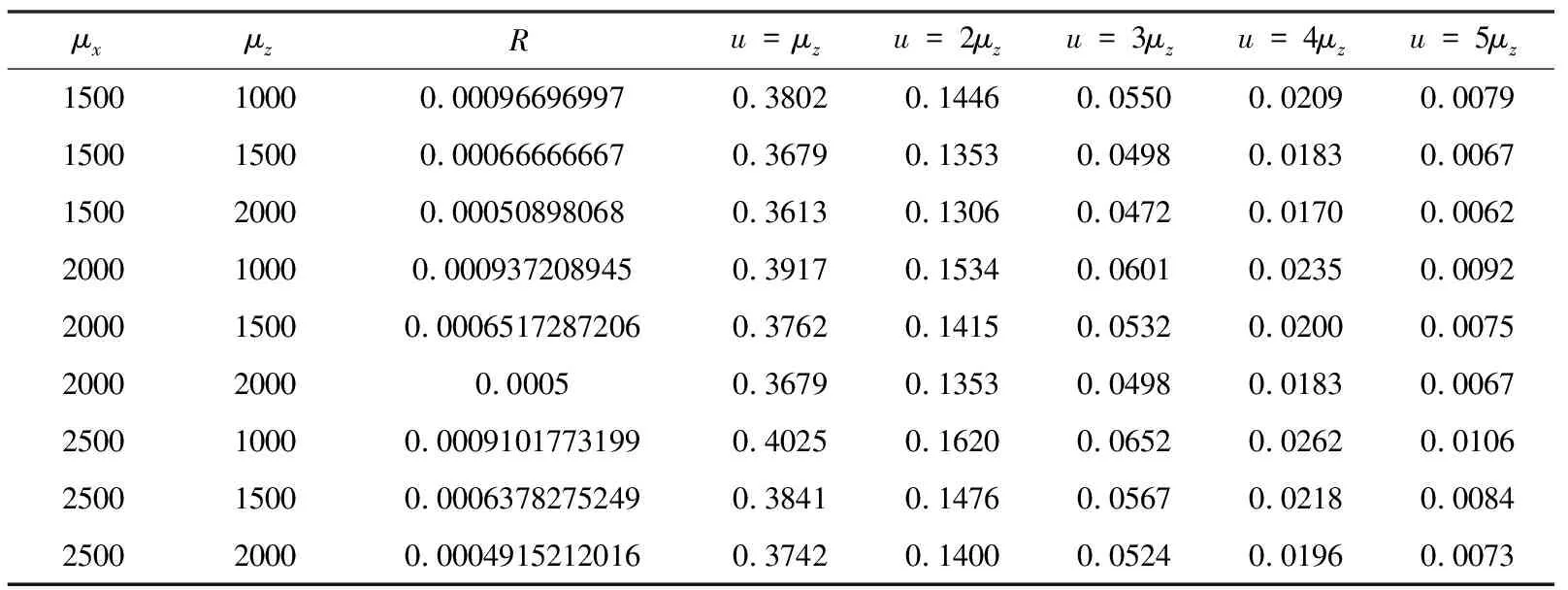
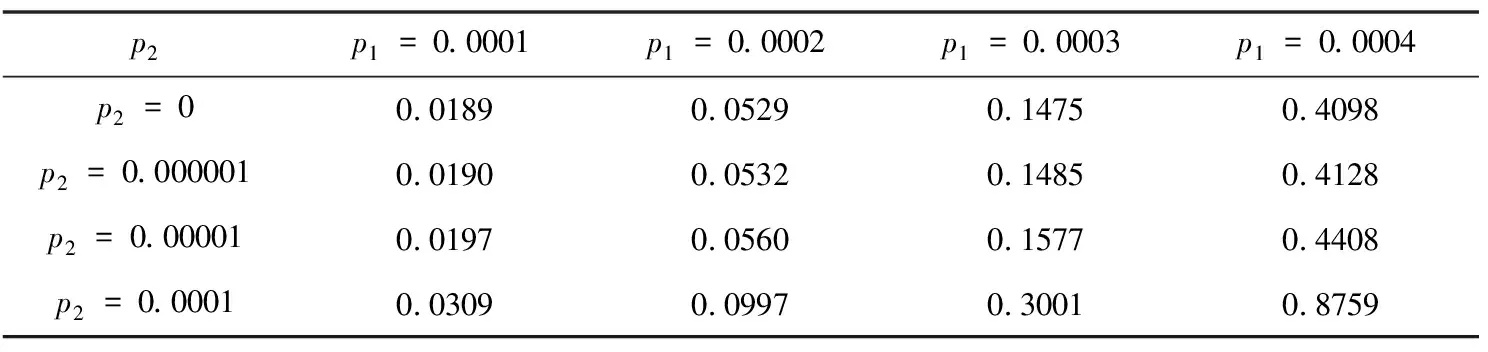
2) {M(t),t≥0}是强度为λ的Poisson过程,{Ni(t),t≥0}是{M(t),t≥0}的pi(i=1,2,3)-稀疏过程,即{Ni(t),t≥0}服从参数为λpi(i=1,2,3)的Poisson过程,其中0 3) 假设{Xk,k≥0},{Yk,k≥0},{Zk,k≥0},{Ik,k≥0}之间是相互独立的,且由文献[11]知{M(t),t≥0},{N1(t),t≥0},{N2(t),t≥0},{N3(t),t≥0}之间也是相互独立的. 记盈利为: (2) 为了保证公司的正常运行,须要求E[S(t)]>0,即μy-p1μx-p2μz-p3μi>0,因此定义相对安全负荷系数 定义T=inf{t:t≥0,U(t)<0}(infφ=∞)称为破产时刻,ψ(u)=Pr(T<∞|U(0)=u)称为最终破产概率. 引理1[13 ]盈利过程{S(t),t≥0}有如下的性质: (1)具有平稳独立增量; (2)E[S(t)]=(μy-p1μx-p2μz-p3μi)λt>0; (3)存在正数r,使得E[e-rS(t)]<∞. 引理2对于模型(1)的盈利过程{S(t),t≥0},存在一个函数g(r),使得E[e-rS(t)]=eg(r)t,其中 (3) LY(r)=E[e-rY],MX(r)=E[erX]. 证明根据Laplace变换和矩母函数的定义知: 故 ·E[exp{-rσW(t)}]=expt{λ[LY(-r)-1]+λp1[MX(r)-1] 再令 即得E[e-rS(t)]=eg(r)t. 引理3方程g(r)=0存在唯一正解R,称其为调节系数. 证明∵g(0)=0, =λ(μy-p1μx-p2μz-p3μi)<0, 证明∀v≤t,根据引理2有 引理4[12]T是ξs停时. 定理2模型(1)的最终破产概率满足Lundberg不等式: ψ(u)≤e-Ru, 其中R为调节系数. 证明因为T是ξs停时,任取t0≤∞,易知t0∧T仍是ξs停时,且有 e-ru=Mv(0)=E[Mv(t0∧T)]=E[Mv(t0∧T)|T≤t0]Pr{T≤t0} +E[Mv(t0∧T)|T>t0]Pr{T>t0}≥E[Mv(t0∧T)|T≤t0]Pr{T≤t0} =E[Mu(T)|T≤t0]Pr{T≤t0}. (4) 因为当T<∞时,有u+S(t)≤0,故 (5) 定理3模型(1)的最终破产概率为 其中R为调节系数. 证明在(4)式中取r=R得 e-Ru=E[e-RU(T)|T≤t0]Pr{T≤t0}+E[e-RU(t0)|T>t0]Pr{T>t0}. (6) 以I{U(t0)≥0}表示集合{U(t0)≥0}的示性函数,则有 0≤E[e-RU(t0)|T>t0]Pr{T>t0}=E[e-RU(t0)I{T>t0}]≤E[e-RU(t0)I{U(t0)≥0}]. 由于0≤e-RU(t0)I{U(t0)≥0}≤1,依据强大数定理可知,当t0→∞时,U(t0)→∞.a.s.所以由控制收敛定理可得 因此在(6)式两端令t0→∞,即可得证结论. 推论1在模型(1)中,设收取的保费Yk,理赔额Xk,退保保单的给付额Zk,支付的红利额Ik分别服从参数为α1,α2,α3,α4的指数分布,则调节系数R满足的方程为: (7) 表1 不同初始准备金u对应的破产概率上界 由表1可以看出初始资本金越多,破产概率就越小,这说明保险公司在条件允许时应尽量增加初始准备金. 例2设λ=20张/天,σ=1,p1=0.5%,p2=0.05%,p3=0.005%,收取的保费Yk,理赔额Xk,退保保单的给付额Zk,支付的红利额Ik分别服从参数为 的指数分布,针对不同的μx,μz,取不同的初始准备金u,利用(7)式得到其调节系数R与对应的破产概率上界e-Ru如表2. 表2 调节系数R与破产概率上界e-Ru的模拟结果 由表2可以看出:当初始准备金和退保额一样时,理赔额越大,破产概率上界就越大,调节系数越小;当理赔额与退保额固定时,破产概率上界随着初始准备金的增加而减低,这与保险公司的实际经营状况完全符合. 例3设保单到达速率为λ=20张/天,σ=1,p3=0.005%,收取的保费Yk,理赔额Xk,退保保单的给付额Zk,支付的红利额Ik分别服从参数为 的指数分布,初始准备金u=10000,取不同的p1,p2得到的破产概率上界如表3. 表3 不同的p1, p2对应的破产概率上界 由表3可以看出当p2一样时,p1越大,即平均索赔比例越大,破产概率就越大;当p1一样时,p2越大,即退保比例越大,破产概率上界就越大.因此,当理赔和退保发生时,保险公司要合理做好相应的工作,减低理赔和退保比例,使公司稳定发展.3 主要结论
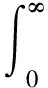
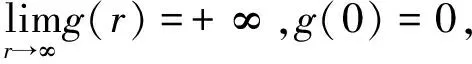
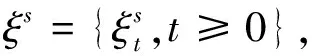
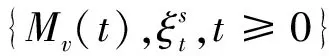

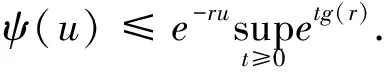
4 几个例子