一类非自治随机时滞系统的状态反馈镇定

*

(1.南京信息工程大学 数学与统计学院,南京,210044；2.湖南师范大学 数学与统计学院,长沙,410081)

1 引言

近年来, 随机时滞系统的研究受到了人们的普遍关注[1-6], 并应用到许多实际工程模型中, 如化学反应系统、交通运输系统以及电力能源系统等.时滞的出现不仅会破坏系统既有的稳定性能, 而且还会为反馈控制器的设计带来不小的障碍.为了解决随机时滞系统的稳定性问题, 人们提出了两种稳定性分析方法, 分别是Lyapunov-Krasovskii泛函法(简称L-K泛函法)[7]和Razumikhin方法[8].目前关于随机时滞系统反馈控制的研究工作, 大多采用L-K泛函法来处理时滞项.由于时滞项参与L-K 泛函的构造, 利用该方法处理时滞往往需要时滞项具有可导性.这在很大程度上限制了研究理论在复杂变时滞系统中的应用.为了处理复杂变时滞, Razumikhin方法引起人们的关注.

作为基于Lyapunov函数的稳定性分析方法,Razumikhin方法在处理变时滞(特别是不可导时滞)的问题上具有独特的优越性.基于非随机的Razumikhin定理, Mao[8]提出了随机系统的Razumikhin理论, 并给出了一些重要的稳定性判据.基于该理论, 王天成和李刚[9]结合反步控制技术[10], 解决了随机时滞系统的状态反馈控制问题; 借助加幂积分器技巧, Wang 等[11]提出了高阶系统的控制器设计策略, 讨论了随机时滞系统的全局渐近稳定性.此外, Min等[12]基Razumikhin方法讨论了参数化随机时滞系统的状态反馈镇定并提出了自适应控制算法.但是, 这些文献所考虑的系统模型仅限于自治系统, 并未考虑非自治的情形.对于非自治随机时滞系统而言, 由于非线性项中显含时间变量t, 系统状态的演变会更加复杂, 自治系统的控制方法已不能实现这类系统的控制目标.因此, 如何实现非自治随机时滞系统的反馈镇定, 仍是一个未解决且有意义的课题.

本文考虑一类非自治随机时滞非线性系统：

(1.1)

其中x=(x1(t),…,xn(t))T∈n是系统的状态,是控制输入,τ(·):[0,∞)→[0,τ]是时滞项,是定义在完备概率空间(Ω,F,P)上的m维Wiener 过程,Ω是样本空间,F是σ代数域,P是概率测度,函数fi:+×i×i→，和gi:+×i×i→m关于t是连续的,关于是局部Lipschitz的, 并且fi(t,0,0)=0,gi(t,0,0)=0,i=1,…,n.

本文目的是通过设计反馈控制器u=u(t,x(t))来实现系统(1.1)的依概率全局渐近稳定[2],即对任意ε>0,有

由于时间变量t的出现,系统呈现非自治的特征,此时控制器的设计难度增加.此外,不同于传统L-K泛函法处理的时滞项,我们这里并未要求时滞项必须可导,这在很大程度上放宽了对时滞项的要求.

基于上述两点,本文将结合Razumikhin方法与反步控制技术来解决非自治随机时滞系统的状态反馈镇定问题, 技术难点总结如下:

1.本文所研究的系统模型的非线性项fi和gi包含时间变量b(t),这对系统的状态响应会产生严重影响,导致控制器本身具有时变性;

2.本文所考虑的时滞项无可导性要求,此时L-K泛函法失效,故我们采用Razumikhin方法来处理复杂变时滞系统的反馈镇定问题.

2 预备知识

下列记号贯穿本文.Tr{X}为方阵X的迹;|X|为欧式空间中向量的2范数；Ci为对应定义域上的i阶连续可微函数全体之集；C1,2([-τ,∞)×n;+)为[-τ,∞)×n上的全体非负函数V(t,x)的集合, 其关于t是C1的且关于x是C2的.

考虑随机时滞非线性系统:

dx(t)=f(t,x(t),x(t-τ(t)))dt+g(t,x(t),x(t-τ(t)))dω,

(2.1)

引理1[6]设x,y为实数,m,n为正实数，则对于任意c>0, 如下不等式成立：

3 主要结果

对系统(1.1)附加如下假设条件:

假设1对每一个i=1,2,…,n,存在一个关于时间t的非负C1函数b(t),使下式成立:

注1与已有文献的假设条件[9,11-16]对比,本文所研究的系统模型考虑了时变因素的影响,即非线性项显含时间变量b(t),假设条件的保守性较小,且容易在实际模型中验证, 具体可见第4节.

(3.1)

其中α1(·),…,αn-1(·)是关于t的非负光滑函数.若假设1成立,则存在一非负光滑函数αn(t)及状态反馈控制器

(3.2)

使得系统(1.1)在[-τ,∞)上几乎处处存在唯一的全局解, 且平衡点x=0是依概率全局渐近稳定的.

1.控制器u的设计及函数αn(t)的选取.

由系统(1.1)和坐标变换(3.1), 我们能够得到如下形式的辅助系统:

(3.3)

其中i=2,…,n,xn+1=u.由于坐标变换(3.1)的可逆性,系统(3.3)与系统(1.1)是等价的.下面将对系统(3.3)进行控制器设计.

首先选取一个C2且正定的函数

由假设1和引理1 可知

其中c1(t)是一个关于t的C1函数, 且满足

选取虚拟控制器

其中λ>0是一待设计的常数,α1(t)是关于时间t的C1的函数.我们有

假设在第k-1步(2≤k≤n)时存在一C2且正定函数

(3.4)

接下来考虑第k步时的函数

(3.5)

由引理1和假设1可得

其中ck1>0是常数,ck2(t),…,ck5(t)是非负C1函数.

将上式代入不等式(3.5)可以得到

令

(3.6)

则有

(3.7)

对于系统(1.1), 考虑如下函数

若设计反馈控制器

其中cn1>0是常数,cn2(t),…,cn5(t)是非负C1函数，则我们有

(3.8)

2.证明系统(1.1)在[-τ,∞)上几乎处处存在唯一的全局解.

由于系统(1.1)与系统(3.3)是等价的,所以只需证明系统(3.3)在[-τ,∞)上几乎处处存在唯一的全局解即可.

结合函数Vn的定义, 由(3.8)可知

(3.9)

(3.10)

3.证明系统(1.1)的平衡点x=0是依概率全局渐近稳定的.

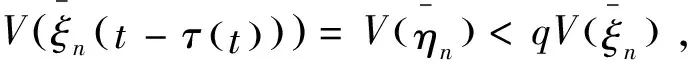
(3.11)

这里μ=4(λ-q).令λ>1,则一定存在q>1,使得μ=4(λ-q)>0.

4 仿真实例

下面将给出两个实例来验证本文的结论.

例1考虑如下形式的系统模型

(4.1)

其中

f1=|sint|x1(t-τ(t)),g1=|cost|x1(t),

f2=g2=x1(t-τ(t)),τ(t)=1.5|sint|.

由于时滞τ(t)不可导, 所以传统文献的控制方法[13-16]不能解决这类系统镇定的问题.容易验证

易知函数f1,f2,g1,g2满足假设1, 故由定理1知存在一时变状态反馈控制器u使得系统(4.1)的平衡点是依概率全局渐近稳定的.

根据(3.1), 我们引入变量及虚拟控制器如下:

进而可以得到系统(4.1)的状态反馈控制器

u=u(t,x(t))=-ξ2α2(t).

(4.2)

设置初值x1(0)=1,x2(0)=-1,我们利用MATLAB 仿真软件在图1和图2中分别绘制了闭环系统(4.1)-(4.2)的状态响应曲线以及控制响应曲线,结果说明所设计的状态反馈控制策略是有效的.

例2考虑一级联化学反应堆系统[18]:

(4.3)

其中x1,x2是两反应堆内的原料量,u是控制输入,R1=0.5,R2=0.5是回流量,Θ1=2,Θ2=2是原料颗粒在反应堆的停留时间,K1(t),K2(t)是反应系数,F=0.5是原料供给率,vol1=0.5,vol2=0.5是反应堆体积,τ(t)=0.25|cost|是时变时滞,δ1=0.5x1(t-τ(t))sint,δ2=-2.8333x2是外部扰动.

类似文献[12]的思路, 我们考虑反应系数K1(t),K2(t)受到随机噪声的影响,即K1(t)=K10+θ1(t)Δ(t),K2(t)=K20+θ2(t)Δ(t),其中K10=K20=0.5,θ1(t),θ2(t)是时变函数,Δ(t)是均值为零、方差为σ2=0.01的Gaussian 白噪声.

由上一节的讨论, 我们可将系统(4.3)转化为下面系统模型:

(4.4)

显然, 系统(4.4)满足假设1, 故由定理1知存在一状态反馈控制器u使系统(4.4)是依概率全局渐近稳定的.

令θ1(t)=sint,θ2(t)=cost,根据(3.1)引入坐标变换及虚拟控制器如下:

于是我们得到系统(4.4)的状态反馈控制器

u=u(t,x(t))=-ξ2α2(t).

(4.5)

设置初值x1(0)=1,x2(0)=-1,我们利用MATLAB 仿真软件在图3和图4中分别绘制了闭环系统(4.4)-(4.5)的状态响应曲线以及控制响应曲线,结果说明所设计的状态反馈控制策略对于系统(4.4)(或者系统(4.3))是有效的.

5 结论

基于Razumikhin方法, 本文研究了一类随机时滞非自治系统的状态反馈镇定问题.通过反步技术, 我们设计了一种时变形式的状态反馈控制器来实现系统的全局渐近镇定.考虑复杂变时滞和时变非线性的影响, 本文在保守性小的镇定条件下给出了反馈控制器的设计策略.