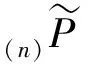Augmented Truncation Approximations for Countable Markov Chains

Li Wendi Liu Jinpeng Liu Yuanyuan

(School of Mathematics and Statistics, HNP-LAMA, Central South University, Changsha, Hunan 410083, China)

Abstract In this paper, we present a survey of the technique of augmented truncation approximation for countable Markov chains.The augmented truncation approximation is a useful method to investigate infinite Markov chains, which is usually used to calculate the stationary distribution and other important parameters for Markov chains.Here we first apply the augmented truncation approximation to study the stationary distribution.We adopt the ergodicity method and the perturbation method to investigate the convergence and error bounds in terms of the total variation norm and the V-norm, respectively.Then, we discuss the augmented truncation approximations of the solution of Poisson’s equation.The convergence to the solution is studied and the truncation approximations to the variance constant in central limit theorems are also considered.These results are illustrated through several examples.Finally possible extensions are discussed in concluding remarks.

Key words Markov chain Truncation approximation Stationary distribution Poisson’s equation

1 Introduction

Let {Xk,k≥0} be a time-homogeneous discrete-time Markov chain (DTMC) defined on the probability space (Ω,F,P) with a countable state spaceE={0,1,2,…}.LetP=(P(i,j))i,j∈Ebe the one-step transition matrix ofXk.Suppose thatPis irreducible and positive recurrent with the unique invariant probability vectorπT=(π(0),π(1),…) such thatπTP=πT,πTe=1, whereeis a column vector of ones. For DTMCs, Poisson’s equation has the following form:

(1.1)

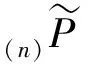
(1.2)

To investigate augmented truncation approximations of the stationary distribution and the solution of Poisson’s equation, two important questions arise naturally:

(i) What conditions ensure the convergence of(n)πTtoπT(or(n)ftof)?

(ii) How to estimate the error between(n)πTandπT(or(n)fandf) for a given truncation sizen?

The issue (i) depends on the property of the original matrixPand the way of augmentation, which may fail in some cases. Examples are given in several literatures, such as [8,15,14], to show that the augmented truncation approximation might not converge to the stationary distribution of the target solution. For the stationary distribution, Seneta [28] is the first one to treat issue (i), and later in [30], he showed that (i) is valid with respect to the total variation norm, that is

‖(n)πT-πT‖→0,asn→∞,

(1.3)

if and only if {(n)πT,n≥1} is tight, which however is not easy to verify for reality models. To avoid the tightness condition, some researchers studiedPwith special property or considered the specific augmentation such as linear augmentation, see Gibson and Seneta [8] for example. Based on (i), Tweedie [31] first addressed the issue (ii) partially. He considered two special augmentations and investigated the upper bound in (ii) for stochastically monotone and geometrically ergodic chains by using the ergodicity method. Without the specifiedPand the augmentation, Liu [15] extended Tweedie’s method to show that (1.3) holds for an arbitrary augmentation under an easily verified sufficient condition, and obtained truncation bounds for stochastically monotone discrete-time polynomially and geometrically ergodic Markov chains. The literatures mentioned above are concerned on the error bounds in the total variation norm. For a vectorV≥e(or function), we are also interested in the convergence in theV-norm, that is

‖(n)πT-πT‖V→0,asn→∞,

(1.4)

and the upper bound of‖(n)πT-πT‖V, where ‖μT‖V=supg:|g|≤V|μTg|=∑i∈E|μ(i)|V(i) denotes theV-norm for the row vectorμT.It is obvious that theV-norm becomes the usual total variation norm whenV=e.TheV-norm may bring new phenomena for the approximations of the stationary distribution. For example, Zhao and Liu [32] proved that the censored Markov chain is the best augmentation in the total variation norm. However, as was shown in [19], it is not necessarily the best one in the sense of theV-norm. Tweedie [31] proposed a computableV-normwise bound for last-column augmentation of DTMCs, which, however, need the assumption of aperiodicity and stochastic monotonicity. Masuyama [22] investigated theV-normwise error bounds for the last-column-block-augmented truncation underf-modulated and exponential drift conditions for a class of continuous-time matrix-analytical models by using the perturbation method. In [18], Liu and Li extended the perturbation method to investigate arbitrarily augmented truncation approximations of invariant probability vectors for DTMCs.

Most of the existing literatures were only concerned about the augmented truncation approximation for the stationary distribution. In fact, compared with the study of the stationary distribution, there are relatively few studies on the solution of Poisson’s equation or other important parameters for Markov chains. Recently, Liu et al. [14] presented a computational framework for the solution of Poisson’s equation of an infinite-dimensional DTMC by developing the technique of augmented truncation approximation.

The rest of this paper is organized as follows. In Section 2, we introduce the augmented truncation approximation for the stationary distribution of DTMCs. The issues (i) and (ii) in terms of the total variation norm and theV-norm are solved by using the ergodicity method and the perturbation method, respectively. In Section 3, we introduce the augmented truncation approximation for the solution of Poisson’s equation. Moreover, truncation approximations to the variance constant in CLTs are also considered in this section. In Section 4, the applications of the above results to single-death processes are given. Numerical examples show that these results are applicable and accurate. In Section 5, we discuss possible extensions of the results in this paper.

2 Truncation approximations for the stationary distribution

In this section, we will focus on both issues (i) and (ii) for the stationary distribution of a DTMC. We consider the bounds in terms of the total variation norm and theV-norm respectively in the following via two different methods: the ergodicity method and the perturbation method.

Now we define some notations. LetB(E) be the set composed of all the subsets ofE.Recall that a setCis called a small set if there is a nontrivial measureνm(B) onB(E) such that

Pm(i,B)∶=∑k∈BPm(i,k)≥νm(B)

(2.1)

for anyi∈Cand anyB∈B(E).A small setαis called an atom if there exists a measureνonB(E) such thatP(i,B)=ν(B) for anyi∈αandB∈B(E).

The following three well-known drift conditions, which are the criteria for positive recurrent, polynomially ergodic chains, and geometrically ergodic chains respectively, are taken from [9] and [26].

(i) D1(V,b,C): Suppose that there exist a finite setC, a positive constantb<∞ and a finite column vectorV≥0 such that

PV≤V-e+bIC,

whereICis the indicator function of setC.

(ii) D2(V,α,c,b,C): Suppose that there exist a finite setC, positive constantscandb<∞,α<1 and a finite column vectorV≥esuch that

PV≤V-cVα+bIC.

(iii) D3(V,λ,b,C): Suppose that there exist a finite setC, positive constantsb<∞,λ<1 and a finite column vectorV≥esuch that

PV≤λV+bIC.

2.1 The ergodicity method

Here we adopt the ergodicity method to address both the issues (i) and (ii), which requires aperiodicity. Thus, we assume that the chainPis aperiodic throughout this subsection.

Now we defineN(C)=min{n:C⊆(n)E} for a finite setC.Fix any statei∈E, by the triangle inequality, we have

(2.2)

for anyn≥max{i,N(C)} and anym≥1.Using (18) in [31] derives

(2.3)

whereΔn(k)=∑j≥n+1P(k,j).The equations (2.2) and (2.3) are the starting point of the analysis of this subsection.

In order to guarantee the convergence (1.3), we first give the following assumption.

Assumption 2.1There exist a finite setC, a constantp∈(0,1) and a probability measureφonEsuch that for anyi∈Cand anyB⊆E, the equation (2.1) holds withm=1 andν1(B)=pφ(B).

The following theorem, which follows from (2.2) and (2.3) and D1(V,b,C), gives a sufficient condition for the convergence (1.3).

We now consider upper bounds for polynomially ergodic chains and geometrically ergodic chains as follows.

(i) ifPsatisfies D2 (V,α,c,b,C) for a non-decreasing functionV, then there exists a computable constantRsuch that

whereM(0)=[V1-α(0)+π(V1-α)]<∞;

(ii) ifPsatisfies D3 (V,λ,b,C) for a non-decreasing functionV, then there exist computable constantsDandγsuch that

where the constantsDandγare given by Theorem 1.1 in [2].

The upper bounds obtained in Theorems 2.3 are not in a preferable form for direct applications. Now we focus on stochastically monotone chains and derive rather explicit bounds for polynomially and geometrically ergodic chains.

Theorem 2.3([15]) Suppose thatPis dominated by a stochastically monotone transition matrixQ, i.e. ∑j>kP(i,j)≤∑j>kQ(i,j) and ∑j>kQ(i,j)≤∑j>kQ(i+1,j) for anyi,k∈Z+.Then for any arbitrary augmentation andn,m≥1,

(i) ifQsatisfies D2 (V,α,1,b,{0}) for a non-decreasing functionV, then

(ii) ifQsatisfies D3 (V,λ,b,{0}) for a non-decreasing functionV, then

(2.4)

2.2 The perturbation method

In this subsection, we adopt the perturbation method to investigate the convergence of(n)πTtoπTin terms ofV-norm from three different aspects: Poisson’s equation, the residual matrix and the ergodicity coefficient.

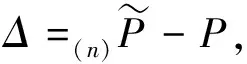
(n)πTΔf=(n)πT[(I-P)f]=(n)πT(g-πTge)=((n)πT-πT)g.

(2.5)

This identity enables us to establish the augmented truncation bounds if we can boundfwell. In order to estimatef, we first give the following assumption.

Assumption 2.2LetC∈B(E) and letα⊆Cbe an atom. Assume thatCandαsatisfy one of the the following relations.

(i) The setC=αis an atom.

The witch listened to all he said and, much pleased, ended by accepting his offer; but she begged him to return to his ship for a little while as she wished to go some way further into the forest, promising to join him later on

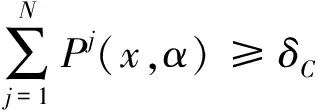
(iii) The setCis aνm-small set such that (2.1) holds andνm(α)>0.

DefineτC=inf{n≥1:Xn∈C} to be the first return time onC.Let Ei[·]∶=E[·|X0=i] be the conditional expectation with respect to the initial statei∈E.The following result, essentially known from [6] and [18], gives a refinement of the bounds onfin some specific circumstances.

Proposition 2.1Suppose that Assumption 2.2 and D3 (V,f,b,C) hold. For any vectorgsatisfying that |g|≤(1-λ)V, Poisson’s equation (1.1) admits a solution, denoted by

(2.6)

For anyi∈E, defineΔn(i,V)=∑j>nP(i,j)(V(n)+V(j)).According to the equation (2.5) and Proposition 2.1, we get the following result on the convergence and error bounds.

Theorem 2.4([18]) Suppose that Assumption 2.2 holds and D3 (V,λ,b,C) holds for a non-decreasing functionV.Then for an arbitrary augmentation we have

‖(n)πT-πT‖V≤H1(n,V),

(2.7)

where

and

Moreover,H1(n,V)→0 asn→∞, and (1.4) holds.

Now, we derive the augmented truncation bounds through a residual matrixUdefined by

U=Pm-υφT,

wheremis a positive integer,υandφTare respectively a non-negative nontrivial bounded column vector and a non-negative nontrivial row vector such thatUis non-negative. The residual matrix was introduced by [11,16] to deal with the perturbation of a Markov operator.

The following drift condition in terms ofUis crucial for the analysis of error bounds.

D4 (V,λ,m): Suppose that there exist a finite vectorV≥eand a positive constantλ<1 such that ‖P‖V<∞ and ‖U‖V≤λ.

Now the convergence and error bounds in terms of the residual matrix are given as follows.

Theorem 2.5([18]) Suppose that D4 (V,λ,m) holds for a non-decreasing functionV.Then for an arbitrary augmentation we have

‖(n)πT-πT‖V≤H2(n,V),

where

and

Moreover, if D3 (V,λ,b,C) holds, thenH2(n,V)→0 asn→∞, and (1.4) holds.

Finally, we adopt the norm ergodicity coefficient Λ(B) to derive the augmented truncation bounds instead of drift conditions, which is defined by

LetV≡e, then Λ(B) becomes the classical ergodicity coefficientτ(B) (see, e.g. [29,27]).

The following result gives the convergence and error bound in terms of Λ(B).

Theorem 2.6([18]) Suppose thatVis a non-decreasing function,πTV<∞,β=‖P‖V<∞, and Λ(Pm)≤ρmfor some positive integermand some positive constantρm<1.Then for an arbitrary augmentation,

(i) ifβ≠1, then

‖(n)πT-πT‖V≤H3(n,m,V),

where

(ii) ifβ=1, then

‖(n)πT-πT‖V≤H3(n,m,V),

where

Moreover, if D3 (V,λ,b,C) holds, thenπTV<∞,H3(n,m,V)→0 asn→∞ and (1.4) holds.

Remark 2.1(i) Compared with the ergodicity method, the perturbation method does not require an explicit estimate of the ergodic convergence rates and even holds for periodic DTMCs, which allows us to relax some restrictions in the ergodicity method. In addition, numerical examples, given in [18], show that the error bounds in terms of the perturbation method are more application and accurate than the bounds in terms of the ergodicity method.

(ii) Each of three upper bounds presented in Subsection 2.2 has its own advantages. In general, the truncation boundH1(n,V) is the worst among the three types of truncation bounds, which, however, is the easiest one to apply in reality models, see [18] for numerical examples. For a specific model, we can choose to calculate the most suitable bound amongH1(n,V),H2(n,V) andH3(n,m,V).

3 Truncation approximations for Poisson’s equation

In this section, we will show truncation approximations of the solution of Poisson’s equation. The solution may not be unique, see [26] for details. Letjbe any fixed state inE.From (2.6), we know thatfjis a solution of Poisson’s equation (1.1), and we work with this version of the solution in the following.

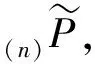
The vector(n)fjdefined above is the unique solution of Poisson’s equation (1.2). For truncation approximations, givenfj, one fundamental issue is to establish the convergence of(n)fjtofj.Sincefjis finite but may be unbounded, we can only consider the pointwise convergence, that is,(n)fj(i)→fj(i) asn→∞ for anyi∈E.

Define the following additive functionals

To ensure the convergence of the solution, it is necessary to make the following assumption.

Assumption 3.1Suppose that for any initial statei∈Eandn≥max{i,j}, both of the following conditions hold:

(i) the sequence {(n)τj} increases and converges toτjwith probability one (w.p.1), i.e.

Pi(ω∈Ω:(n)τj(ω)↑τj(ω),asn→∞)=1;

(ii) the sequence {(n)ζj(|(n)g|)} increases and converges toζj(|g|) w.p.1, i.e.

Pi(ω∈Ω:(n)ζj(|(n)g|)(ω)↑ζj(|g|)(ω),asn→∞)=1.

Now we give the convergence of the solution, please refer to [14] for the proof.

Theorem 3.1([14]) If Assumption 3.1 holds, then we have, for anyi∈E,

where(n)fj(j)=fj(j)=0.

Letg=eiin (3.3) of [14], we have the following interesting corollary directly.

Corollary 3.1If Assumption 3.1 holds, then we have, for anyi∈E,

The solution of Poisson’s equation can be used to express the variance constant, which is a very important parameter in CLTs. Therefore, based on Theorem 3.1, we now consider the convergence of the variance constant. Recall that a CLT holds if there exists a constant0≤σ2(g)<∞such that for any initial distribution

whereN(0,σ2(g)) denotes a normal random variable, “⟹” means convergence in distribution, and the constantσ2(g) is called the variance constant. From [26], we immediately know that ifπT|g|<∞, then a CLT holds if for some (then for all)l∈E,

(3.1)

and if a CLT holds, then the variance constant is given by

The result on variance constant is given as follows, please refer to [14] for details.

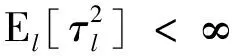
where(n)σ2((n)g) is the variance constant of the chain(n)Xk.

According to the sample path analysis, we show that Assumption 3.1 holds for two types of truncation approximation schemes: the censored chain and the linear augmented truncation.

The transition matrix of the censored Markov chain on(n)Eis given by (see e.g. Page 118 of [12])

(3.2)

wherePE1,E2=(P(i,j))i∈E1,j∈E2forE1,E2∈B(E), and(n)ECis the complement set of(n)E.

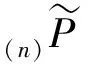
For the fixed statej, the transition matrix of the (j+1)th column augmented Markov chain is given by (see, e.g. [30])

(3.3)

where(n)ejis a (n+1)-vector with unity in the (j+1)th position, zeros elsewhere.

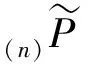
4 Applications

In this section, we will apply our results to the single-death process, which is classical asymmetric Markov process including the birth-death process and the embeddedM/G/1 queue. The single-death process has a special transition matrixPgiven byP(i,i-1)>0 for alli≥1 andP(i,i-k)=0 for alli≥k≥2.We will give the error bounds for the stationary distribution of the embeddedM/G/1 queue and the exact expression of the solution of Poisson’s equation for a general single-death process, respectively.

4.1 The embeddedM/G/1 queue

First, we consider a general transition matrix ofM/G/1 form (see, e.g. [17]) given by

(4.1)

which includes the transition matrix of the embeddedM/G/1 queue as a special case.

We will make the following assumption.

Assumption 4.1Assume that

(i) the transition matrix (4.1) is irreducible;

(iii) min{φA,φB}>1 andφA<∞.

From Proposition 3.1 in page 318 of [1], it is not hard to derive that the chain is positive recurrent if and only if (i) and (ii) of Assumption 4.1 hold. Assumption (iii) is imposed in order to find a drift condition D3 (V,λ,b,C).

To apply Theorem 2.3 (ii), we need to make some assumptions in addition to Assumption 4.1. We assume thatPis aperiodic andA(φA)=∞ andB(φA)<∞.Then there exists a unique solution (s0,z0) to the following equation

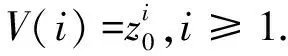
Now we determine the value of the parameterd.Define an atomαbyα={0}.IfC⊆α, thenCis an atom. From Proposition 2.1, we know thatd=0.Otherwise, ifC={0,…,k} fork≥1, we can obtain that for anyi∈C

Letν(B)=χ1ωα(B) for anyB∈B(E), where

Obviously,ν(B) is a nontrivial measure onB(E).Furthermore, ifχ1>0, thenCis a small set, and from Proposition 2.1, we know that

Based on the above arguments, applying Theorem 2.4 yields an upper boundH1(V,n) directly.

4.2 General single-death processes

Now, we consider the explicit expression of the stationary distribution and the solution of Poisson’s equation for single-death processes. To solve Poisson’s equation, we need to introduce the following notations (see e.g. [33]):

and

We simply denotehmbyhm(e).

The result can be found in the survey paper [33]. However, the arguments in the proof are new.

Proposition 4.1Suppose that the single-death processXkis irreducible and positive recurrent. Then, there exists a unique invariant probability given by

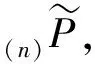
(4.2)

Using the induction, for the case ofi=1, we have

Assume that (4.2) holds for allm≤i

in which the fourth equation follows by using the fact

It follows fromπTe=1 that

Then from Corollary 3.1, we obtain the assertion.

In the following theorem, we present the explicit expression of the solution of Poisson’s equation for general single-death processes.

Theorem 4.1Suppose that the single-death processXkis irreducible and positive recurrent. If the functiongsatisfiesπT|g|<∞, then for any fixed statej∈E, we have

ProofIn the follows we will solve (1.2) with(n)fj(j)=0.From Corollary 2.3 in [33], one easily shows

Since(n)f(j)=0, by using the induction, it follows that

and

Then, we obtain the solution of Poisson’s equation (1.2).

From Theorem 3.1, we have, fori

The case ofi>jcan be verified similarly. Thus the assertion is proved.

5 Concluding remarks

The technique of the augmented truncation approximation provides us an efficient way to approximate the steady performance measures, such as stationary distribution and the solution of Poisson’s equation, for infinitely countable DTMCs. It is direct to extend these results from DTMCs to CTMCs with bounded generators. However, as has been shown in [14] and [18], one has to be careful with the unbounded cases which may cause essential difference from the discrete-time cases.

Markov chains considered in this paper are on one-dimensional countable state space. Naturally, we want to extend the technique of the augmented truncation approximation to a Markov chain on a high-dimensional or continuous state space. In [3], Bean and Latouche investigated the issue (i) of a two-dimensional quasi-birth-and-death process, but the issue (ii) is still an open problem. Jiang et al. [10] applied the augmented truncation approximation to study quasi-birth-and-death processes on a continuous state space. However, both the issues (i) and (ii) have not be studied for continuous state Markov chains. It is a quite interesting topic which is worthy of further research.

The quasi-stationary distribution has been used for modelling the long-term behaviour of stochastic systems, which, in some sense, terminate, but appear to be stationary over an reasonable time scale. The augmented truncation approximation can be also used to compute the quasi-stationary distribution for an absorbing transient Markov chain, see e.g. [5]. Recently, we [13] have made some progress in approximate the quasi-stationary distribution for Markov-modulated Markov chains. However, many issues in this area keeps unsolved, which may be a topic for our research.