随机双曲折现下的消费与最优投资策略探究
*
(1.中南大学数学与统计学院,长沙,410083;2.中南大学商学院,长沙,410083)
1 引言
最优消费与投资的问题是金融数学学中的一个重要的研究方向.在1969年,Samuelson考虑了离散时间下的投资者最优投资组合选择与消费行为的问题[1],与此同时Merton将Samuelson的模型扩展到连续时间情形,并讨论了当收益率由一个Wiener Brownian运动过程生成时多资产组合的最优配置与不确定性下的投资者跨期消费行为[2].之后的研究者在Merton的不确定性条件下的最优消费与投资组合研究的基础上进行了一系列的推广与拓展.Basak等分析了效用对打的最优动态投资组合与消费者消费行为的关系,提出了使用损失预期的替代风险管理模型弥补风险价值模型过度偏好风险的不足[3].Cox与Huang等研究了资产价格服从扩散过程时的最优消费与投资组合[4].Choi等研究了生存时间无限时,投资者消费休闲和退休选择与最优投资组合的关系[5].考虑到消费率通常大于或等于一些非负过程,Yuan等研究了具有消费习惯约束的最优消费与投资组合策略[6].在具有马尔可夫切换的金融市场中,Fei推导了广义Ito公式,并利用带有马尔可夫切换的广义Hamilton-Jacobi-Bellman(HJB)方程计算了不确定随机金融市场下具有马尔可夫切换的最优消费与投资组合[7,8].Mao和Carson将挣钱投资拓展到保险行业,得到了保险合同的最优价格与保险公司最优投资组合之间的关系[9].Lee等研究了在生存相对消费约束下的常数相对风险厌恶(CRRA)效用函数控制时,在投资者生存时间无限的情形下的选取最优消费与投资组合的问题,并提供了其解析解[10].Chang等人使用Legendre多项式,将非线性的HJB方程转化为线性对偶形式,并获得了其在Vasicek利率模型下最优消费与投资组合的解析解[11].Song等讨论了在损失厌恶和下行消费约束下的连续时间最优投资组合与消费问题,数值试验表明规避风险的投资者喜欢消费更多的钱,但比恒定相对风险厌恶的投资者承受的风险更少,另外恒定相对风险厌恶的投资者的最优财富下降速度通常会更快[12].Lim等讨论了退休前后不同的最佳消费与投资组合的策略,并给出了其闭解[13].
为了简化模型,在跨期经济研究中通常使用具有常数折现率的指数折现函数,Strotz在1955年提出了一个具有时间一致偏好的折现函数[14].但是,一些心理学与行为科学的研究指出,由于时间推移,消费者对产品的心理预期会发生一些变化,因此时间一致偏好通常的假设难以被满足[15,16].在此基础上,Harris和Laibson为了反映消费者心理预期的变化,提出了随机双曲折现模型,允许消费者的心理预期在持续一段时间后发生转变,使得模型更符合实际生活[17].Palacios与Huerta等研究了资产组合的选择问题[18],王等研究了双曲折现假设下的消费与套期保值问题[19].陈等将随机双曲偏好引入Morten经典的跨期消费与投资组合选择模型,得到了在常数绝对风险厌恶效用函数假设下的最优消费与投资组合问题的解析解[20].Koo与Lim研究了基于双曲折现和税收时间不一致偏好的假设下的消费与人寿保险的最优投资策略[21].
现实世界中的一些随机因素通常也会对人的消费行为产生影响.消费行为可以被认为服从一个Wiener Brownian运动过程,因此随机消费作为一个重要的影响因素需要被加入到模型中.贺芳等研究了在随机消费的情形下的保险基金投资问题[22].江和马提出一个具有随机消费的风险模型用于计算破产概率[23].本文提出基于随机消费模型的投资者消费和资产配置策略,在投资者具有常数绝对风险厌恶效用函数的假设条件下,研究具有时间不一致偏好和生存期无限的投资者个人跨期消费与资产投资组合的配置问题,并给出模型的解析解.
2 双曲折现下的随机消费模型
在这一节中,我们首先回顾随机双曲偏好模型,然后,在Morten提出的连续时间消费投资模型的基础上引入随机消费行为,建立一个随机消费与最优投资组合选取的模型.
2.1 随机双曲偏好模型
Harris和Laibson在2013年提出了随机双曲偏好模型.折现区间按照时间间隔被划分为当前区间和未来区间两个子区间,在当前区间中,收益按照恒定的折现率δ的指数折现函数进行折现;同时,在以恒定折现率δ的指数折现的基础上乘以时间一致偏好因子β作为在未来区间的折现函数.那么,这个双曲折现函数的表达式可以写为如下形式:
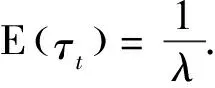
这时,随机双曲折现函数转化为一个确定性的跳跃函数,称为瞬间满足折现函数(IG).时间一致偏好因子β∈(0,1]用来描述偏好随时间变化产生的偏差程度:β越小,则当前时间区间与未来时间区间的偏好之间偏差越大;β=1时,当前时间区间与未来时间区间的偏好不存在偏差,这时,随机双曲偏好模型退化为常数指数折现偏好模型.当时间t→0时,我们有:
这说明随机双曲折现函数对于时间t的平稳性假设是满足的.
2.2 消费投资模型
假设金融市场在时间区间[0,T]内是一个有借贷限制的完备市场,其中包含有风险资产和无风险资产,投资Zp(t)和消费Zc(t)是两个在完备的概率空间(Ω,F,P)上相互独立的标准布朗运动.假设在t时刻一个固定回报率为r的无风险资产的价格St满足如下微分方程:
dSt=rStdt.
同时,对于有风险资产,假设在t时刻的价格Pt服从标准布朗运动,即满足微分方程:
dPt=Ptμpdt+PtσtdZp,
其中,μp,σt分别是有风险资产回报的均值和方差.
假设投资者在终止时刻T之前退休,在任意t∈[0,T]时刻随机地进行消费,且随机消费Ct满足下列微分方程:
(1)
其中,μc和σc分别是消费额的均值与方差,|ρ|<1是投资者消费额与其拥有的风险资产价值间的相关系数,是一个常数.在t时刻,我们记投资者用于投资风险资产的财富数量为θt.为了便于计算,假设投资者仅拥有初始财富W0>0,没有工资收入.那么在无限生命周期内,其所有资产价值的变化过程满足如下方程:
dWt=(rWt+(μp-r)θt-Ct)dt+σpθtdZp,
其中,Wt表示投资者在t时刻拥有的财富.
这时投资者的目标是选取最优的资产配置组合来得到期望效用函数的最大值,即:
(2)
其中,u(c)为效用函数,τ是一个参数为λ的指数分布随机变量,W0=w,C0=c.
3 双曲折现下的随机消费模型的策略求解
定理假设投资者具有常数绝对风险厌恶效用函数:
其中,绝对风险厌恶系数η>0,则投资者用于投资风险资产的财富的最优值为:
证明基于Palacios和Perez提出的双曲折现模型,使得期望效用函数最大的解θ*需要满足如下HJB方程[18]:
(3)
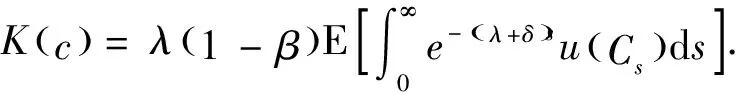
对上式右边方括号中的函数关于变量θ求导,其导数记为f(θ),得:
f(θ)=(μp-r)Vw+σp2θVww+σpσcρVcw.
令f(θ)=0,即可得到(3)式右边函数的一个极值点:
(4)
由于投资者具有常数绝对风险厌恶效用函数:
不妨假设值函数V(w,c)具有如下形式:
(5)
分别计算其各阶偏导数,得:
Vt=0,
Vw=e-ηr(w+bc+a),
Vw=-ηre-ηr(w+bc+a),
Vc=be-ηr(w+bc+a),
Vcc=-ηrb2e-ηr(w+bc+a),
Vcw=-ηrbe-ηr(w+bc+a).
将它们代入(4)式中,得到:
(6)
现在将(1)式使用差分进行近似,得到:
(7)
再将(3),(6),(7)式代入K(c)的表达式中,得:
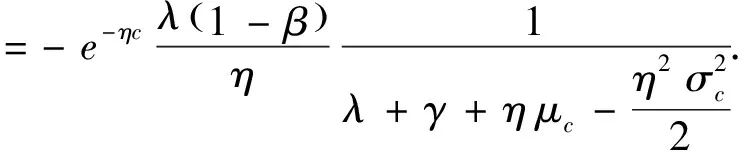
(8)
整理(5),(6),(8)式并代入(3)式的HJB方程中,得到:
(9)
整理可得:
(10)
(11)
令(10)式等于0,即可得到:
类似地,令(11)式等于0,可得到:

其中
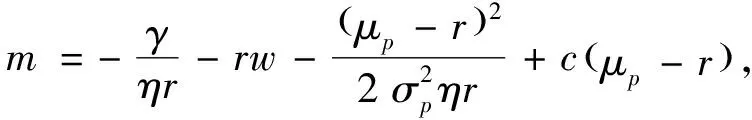
于是,得到最优的用于投资有风险资产的财富数量为:
定理证毕.
以下我们给出该最优值θ*的几个性质.
性质1θ*与随机双曲折现模型中的参数δ和β无关,仅由μC,μp,σp,σc,ρ,r以及风险厌恶系数η决定.因此,在随机消费模型下,用于投资风险资产的资产总额与投资人的时间偏好无关.
性质2 当投资过程与投资者的消费行为无关,即ρ=0时,最优的投资策略为:
此时,用于投资有风险资产的财富数量与风险资产的方差σp,风险资产的超额收益率μp,风险厌恶系数η以及无风险利率r有关.用于投资有风险资产的比例为:
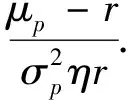
性质3 当ρ=0时,用于投资风险资产的财富与无风险利率r成反比,随着无风险利率的增高,投资人会将更多的资产用于购买无风险资产,这也与实际生活中人们普遍的投资心理吻合.
4 总结与展望
本文研究了随机双曲折现下的消费行为与风险资产投资组合配置的问题.在前人的基础上,我们进一步假设消费过程是一个服从Wiener过程的随机行为,在消费的效用函数为常数绝对风险厌恶函数的情形下,求得了最优资产配置策略的近似解.同时,我们对得到的近似解进行分析,发现用于投资有风险资产的最优财富量是一个与双曲折现函数无关的常数,且与随机消费行为以及风险资产自身的性质密切相关.特别地,当随机消费行为与风险资产相互独立时,用于投资有风险资产的最优资产量与其他研究者的结果吻合.在未来的工作中,我们还可以进一步将个人的无限生命周期改为有限时间段,并且考虑投资者的劳动收入等.

