超声换能器声场的快速数值模拟与声透镜的优化设计

(西安电子科技大学 微电子学院，西安，7100071)

1 引言

高频的超声换能器声场建模一直是一个困扰超声换能器优化设计和研制的难题[1-5].利用COMSOL等有限元仿真软件进行高频超声换能器的仿真需要耗费大量时间，随着仿真频率的提高，消耗时间会指数上升.超声换能的器设计参数众多，使用有限元模拟方法对其进行优化设计不利于缩短研发周期.此外，超声声场调控在生物成像、神经调节、粒子操纵和无损检测中起着至关重要的作用[6-8].利用超材料透镜，控制声场的每一个网格点的相位，从而实现声场调控是一个比较热门的方法.

角谱传播方法在光场的快速建模方面具有显著成效，可以将其应用到声场的快速建模中.基于角谱传播方法，利用COMSOL等有限元仿真软件或利用水听器等手段得到的表面声场进行传播计算，可以快速得到超声换能器声场传输的二维/三维信息，比有限元软件仿真速度有大幅提升.Gerchberg-Saxton迭代算法[9,10](后文简称GS算法)是一种检索光分布相位的方法.类似地，可以将GS算法用于声场相位的计算，结合声场快速建模方法实现声全息表面的快速调控.

本文建立一种基于角谱法的超声换能器声场快速建模算法，可以完成超声换能器声场的二维/三维快速建模.此外，结合角谱法和GS算法，优化声全息透镜，实现超声换能器声场调控.

2 基本原理

2.1 角谱概念

对于一维时域声场u(t)，其存在固有的属性如周期T，频率f，同时，可以计算得到其空间角频率ω=2πf=2π/T.同理，对于空间中深度为z处的平面二维声场U(x,y,z)，也会存在空间周期λ，空间频率fs，及空间角频率k=2πfs=2π/λ.k亦称为波矢.

对一随时间变化的信号u(t)进行傅里叶变换，得到的是该信号的频谱分布；对空间中深度为z处的平面二维声场U(x,y,z)进行二维傅里叶变换，则可以得到其空间频谱分布.由于各个不同空间频率的傅里叶分量，可看作沿不同方向传播的平面波，因此，也可称其为平面波的角谱.

2.2 角谱与二维傅里叶变换

空间中深度为z处的一个单频单向(方向为k0)的平面波声场U0(x,y,z)可表示为：

=A0exp[j2π(fx0x+fy0y+fz0z)],

(1)

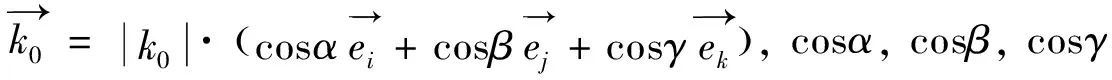
式(1)可以化为：

从上式提取前两个因子得到声场某一方向的角谱AS(angle spectrum)：

若考虑一个z平面(即z=z的平面)中可以自由传播的单频平面波声场U(x,y,z)，则其与角谱AS(fx,fy,z)有如下关系：

上式即为单频平面波声场的二维傅里叶变换，其逆变换如下：

2.3 基于角谱法(ASM)的声场快速建模

由于自由传播的声场U(x,y,z)为稳态声场，满足亥姆霍兹(Helmholtz)方程，故我们得到以下方程组[11-14]

可求得其特解

(2)

其中，AS(fx,fy,0)表示位于平面z=0的声场U(x,y,0)对应的角谱.

通过式(2)，我们看到z平面内声场的角谱与振幅和频率无关.在理想情况下，声场在传播过程中仅发生相位改变，振幅不变.此外，将角谱与传输距离z相关的项提取出来，可以得到传输函数H(z)的表达式：

波数k在x,y轴上的投影分别为：

对某一特定尺寸声场，kx的取值范围为：

其中，M为初始声场采样点的数量，L0为初始声场在x轴方向上的宽度(默认x轴和y轴宽度相等).ky的取值范围类似.

对于不满足此条件的kx,ky，将传输函数置零，相当于实现了空间滤波.

综上所述，我们利用角谱方法获得超声换能器三维声场的步骤为：

1)对初始平面进行二维傅里叶变换得到z=0平面的角谱；

2)利用不同z平面的传输函数，得到一系列z平面角谱；

3)利用逆傅里叶变换，得到不同传输深度z的声场.

2.4 基于角谱法与GS算法的声场调控

提出GS算法是为了解决光场调控的问题，将其与角谱传输进行结合，即可很好实现对声场的相位调控.不断地迭代z平面的声场幅值，得到相应的z=0平面相位φ0，然后通过下述公式(3)，(4)，将相位转换为透镜厚度T，利用透镜改变初始声场相位，从而实现目标平面的声场调控[12,15]：

T(x,y)=T0-ΔT(x,y),

(3)

ΔT(x,y)=Δφ(x,y)/(km-kh),

(4)

式中，T0为透镜初始厚度，是由传输介质(通常为水)和透镜材料2π相位波程差确定，kh是全息(Hologram)透镜材料波数，km是传输介质(通常为水)的波数，Δφ(x,y)是透镜产生的相位差.

利用GS算法进行迭代的流程如图1所示，具体步骤如下：

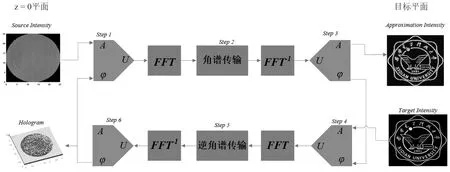
图1 通过GS算法迭代求出调控换能器声场透镜流程图

1)通过COMSOL或利用水听器测量得到初始声场U(x,y,0)，默认初始相位φ0为0；

2)利用角谱传输，得到指定z平面内的声场U(x,y,z)，提取其幅值Az和相位φz；

3)判断输出幅值Az和目标图像幅值Atarget间误差是否满足要求，是,则输出此时的透镜厚度T，否则继续迭代，将相位φz给到步骤4)；

4)利用目标图像幅值Atarget，和当前平面相位φz得到一个新的z平面声场；

5)利用逆傅里叶变换以及逆角谱传输得到新的z=0平面相位φ0；

在步骤6)中，如果考虑透镜材料带来的衰减，则衰减系数可以利用如下公式计算[15]：

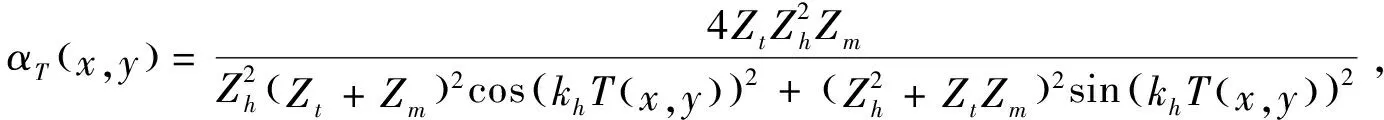
其中，Z代表材料声阻抗，可利用材料声速与密度的乘积求得.下标t，h，m分别指代换能器材料、全息透镜材料、传输介质材料.在步骤6)中重新生成迭代的初始声场为：

3 模型应用与实验

3.1 声场快速建模

图2(a)为换能器归一化表面声场，利用水听器测得，中心频率为1MHz，尺寸为直径25mm的圆形.图2(b)为利用角谱传播算法计算得到的归一化三维截面声场，分别为x，y轴中心零点处截面.

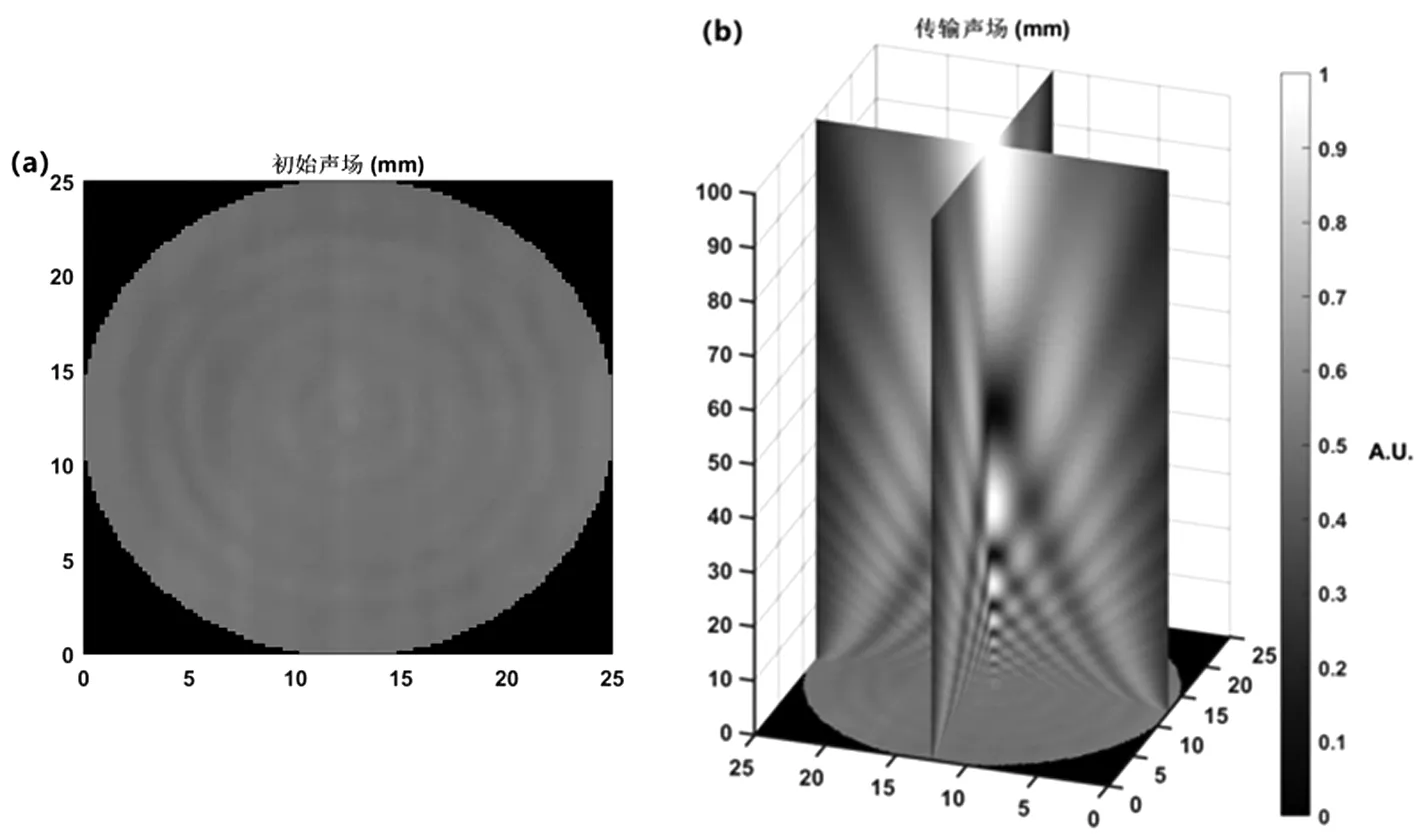
图2 (a)利用水听器测得表面声场；(b)使用ASM实现快速三维建模

3.2 声场调控

利用如图3(c)所示初始声场，通过角谱迭代的方式，使特定z=3cm平面的声场幅值靠近目标图3(a)，最终输出归一化声场幅值为图3(b)所示.图3(d)为通过透镜校正后初始平面的归一化声场，图3(e)为输出声全息透镜的三维模型，带有正方形外壳.通过3D打印技术可以制备出所需要的透镜，进而实现超声换能器的声场调控.

图3 (a)反演目标图像；(b)反演输出(归一化)图像；(c)初始声场；(d)反演后的初始声场；(e)输出透镜

4 总结

本文基于角谱法实现超声换能器声场的快速建模，对于高频换能器声场的三维建模，该方法可以有效提高仿真效率.结合GS算法，可以优化出到声学全息表面的透镜，实现超声换能器声场的准确调控.但是，该方法只能对单频平面波声场进行计算，且要求为纵波.当换能器存在其他振动模态，产生横波、表面波等非纵波时，实际结果会与仿真计算结果产生很大误差.同时，利用COMSOL等软件，或者利用水听器等设备得到声场，消耗时间仍较长.在后续研究过程中，可以使用瑞利积分等方式来计算超声换能器初始声场、利用多个频率声场叠加的方法来解决上述问题.