基于指数平滑与CEEMDAN 的混合储能控制策略研究

周 强， 蔡嘉炜， 江修波， 郑文迪

（1.福州大学 电气工程与自动化学院， 福建 福州 350108；2.国网福建省电力福州供电公司， 福建 福州 350003）

0 引言

随着环保理念的深入普及和国家相关政策的支持，我国电力能源消费结构正在逐步发生变化，以风电为代表的清洁能源正广泛地应用。 由于风力发电受到诸多方面的限制，其发电出力具有一定的随机性、间歇性和波动性。 风电大规模地接入电力系统， 若不采取相应的应对措施，则会影响电力系统的稳定运行。 因此，给风电站配置一定的储能系统，可以防止风电并网对电力系统 的 稳 定 造 成 影 响[1]，[2]。

依据充放电特性的不同， 储能装置分为两类：功率型储能和能量型储能。 功率型储能以超导磁储能、超级电容器和飞轮储能为代表，能量密度高，响应速度快，循环寿命长，但容量小。 能量型储能以锂电池、 蓄电池和钠硫电池为代表，能量密度大，成本低，充放电时间长，但响应速度慢，循环寿命短。 采用混合储能方式可充分利用装置的优势互补特点，平抑风电波动，使电网能满足国家标准的相关要求[3]。

国内外研究者对利用储能平抑风电波动的问题开展了大量的研究， 也取得了较多的成果。文献[4]采用低通滤波分解储能功率，但其滤波时间常数难以控制。 文献[5]运用小波变换，依据分频原则对储能功率进行合理分配， 利用双层模糊控制将荷电状态控制在合理范围。 文献[6]提出一种自适应小波包对储能功率进行初级分解， 根据超级电容荷电状态进行二次修正。 文献[7]利用经验模态分解（EMD）对混合储能功率进行分解，依据荷电状态调整滤波阶数， 但该方法存在模态混叠的问题。 文献[8]提出了模糊聚类模态分解功率方法，但存在计算量繁杂等相关问题。文献[9]提出总体经验模态分解储能功率方法， 并根据滤波阶数实现储能间功率合理的分配。

为了解决上述问题， 本文提出一种自适应噪声的完整集合经验模态分解（CEEMDAN）的储能控制策略方法。 首先，应用CEEMDAN 将储能功率进行分解， 找到次高频和高频分量重构的分界点；然后，由能量型储能装置吸收次高频分量，由功率型储能装置吸收高频分量；最后，根据荷电状态自适应调整分界点， 从而实现储能内部协调稳定运行。

1 风电并网功率分解

1.1 风电联合储能系统拓扑图

风电联合储能系统拓扑如图1 所示。 该系统由风力机、逆变器、混合储能装置等组成。 风力机发电功率也许不能满足并网的相关标准要求，须借助储能装置平抑其波动性使其达到要求。 储能装置主要由电池和超级电容组成，电池平抑波动性变化较缓慢的部分，超级电容平抑波动性变化较快的部分。 运用混合储能装置能较好地吸收波动部分，减少对电网的冲击，保证电网的正常稳定运行。

图1 风电联合储能系统拓扑图Fig.1 Wind power combined energy storage system topology

图中：PWind为风电实际出力；PG为平抑后的功率；PHess为混合储能平抑的功率，当PHess＞PG时，储能装置吸收多余的波动功率，反之，储能装置发出功率；PSc为超级电容的功率；PB为电池功率。

功率计算公式：

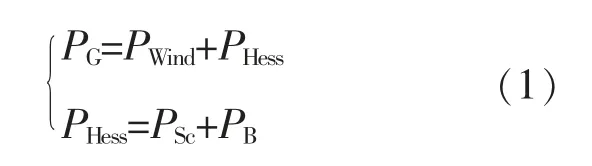
1.2 指数平滑法

指数平滑法是根据上一时刻的平滑数据与当前时刻的实际数据进行加权处理，将处理后的数据作为当前时刻的平滑值。 该方法容易处理随机波动的信号，信号平滑效果较好。 因此，风电实际出力要满足国家并网波动的要求，指数平滑法的应用十分重要。 指数平滑法的公式如下：

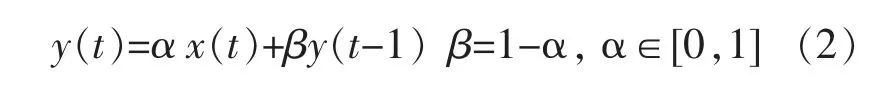
式中：x（t）为t 时刻的风电实际数据；y（t）为t 时刻平滑后的数据；α 为平滑系数。

首先判断风电数据是否满足并网条件。 若满足并网条件，则直接并入电网，储能装置既不吸收功率也不放出功率；若不满足条件，则划分平滑系数区间，从平滑系数α 最大值开始；经过指数平滑后仍不满足并网条件，则继续减小平滑系数α，直到满足并网标准为止。 剩余波动部分的功率由储能装置平抑，其流程如图2 所示。

图2 指数平滑风电的流程图Fig.2 Flow chart of exponential smoothing wind power

2 混合储能功率分配

2.1 完备总体经验模态分解

CEEMDAN 是在EEMD 的基础上加以改进的，EEMD 是为了克服传统EMD 中模态混叠效应问题而改进的算法[11]，[12]。 EEMD 方法是通过多次对原始信号加入白噪声进行EMD 分解， 将多次分解的数据进行平均获得固有模态分量。 由于EEMD 多次添加噪声以及多次计算， 增加了计算量和重构误差。 CEEMDAN 方法是在信号中添加正反噪声， 可以有效地减少运算量和重构结果的信号误差。 因此，采用总体经验模态分解方法，可以解决重构误差低和效率低的问题。

CEEMDAN 分解步骤如下。

①在原始信号中添加正反成对的白噪声ni（t），将添加噪声的信号进行m 次分解，成为多个一阶分量IMF1i和残差r1（t）：

②求取m 次分解所得的一阶固有模态分量的均值，得到最终IMF1i：

③将一阶残差r1（t） 添加正反成对的白噪声ni（t），进行m 次分解成多个二阶分量IMF2i和残差r2（t）：

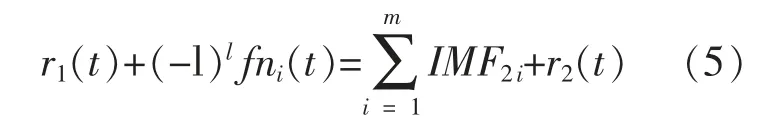
④同理，对残差r2（t）进行分解，直到不能分解为止，最终得出分解结果：

2.2 互信息熵

互信息是源于信息论中的一种度量， 它主要用于衡量两个随机变量之间的统计依存性[10]。 两个随机变量之间的依存性越大， 所包含的信息量越多；反之，信息量越少。

相邻分量的固有模态函数之间的信息熵表达式：

式中：H（IMFn）为第n 个固有模态分量的熵；H（IMFn，IMFn+1）为联合信息熵。

根据信息论的相关内容可知， 两个随机变量相互独立，其信息熵应等于零。 由此可知，相邻的固有模态分量的信息熵从高频到低频排列为先减小后增大， 即在这个过程中必然会出现一个极小值。 本文根据该知识点找出高频分量与低频分量间的临界值。 临界值kmi的相关表达式如下：

式中：extremum 为极值 函 数；I（IMFn，IMFn+1）-，I（IMFn+1，IMFn+2）+分别为信息熵递减、递增。

混合储能功率经过CEEMDAN 分解成频率依次按高到低排列的不同模态分量； 通过互信息熵找到模态分量之间信息熵的极小值； 依据极小值可重构出高频功率和低频功率； 再将重构功率分别经过超级电容和电池进行吸收，即：

式中：PSc为超级电容的功率；PB为电池的功率；IMFn为第n 个固有模态分量；r 为余量；g 为固有模态分量的总数。

2.3 自适应调整荷电状态

为了描述储能系统运行的工作状态而引入荷电状态的定义。 荷电状态即为储能的剩余容量与额定容量的比值：

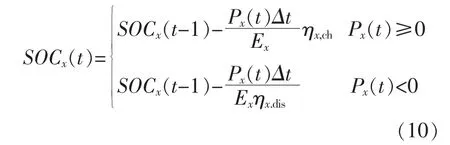
式中：SOCx（t），SOCx（t-1）分别为储能装置在t 时刻、t-1 时刻的荷电状态；Px（t）为储能装置在t 时刻的充放电功率，Px（t）＞0 表示放电，Px（t）＜0 表示充电；Δt 为相邻时刻的间隔；Ex为储能的额定容量；ηxch，ηxdis分别为充、 放电效率；x 为B 表示电池，x 为Sc 表示超级电容。

根据式（11）进行储能额定容量配置：

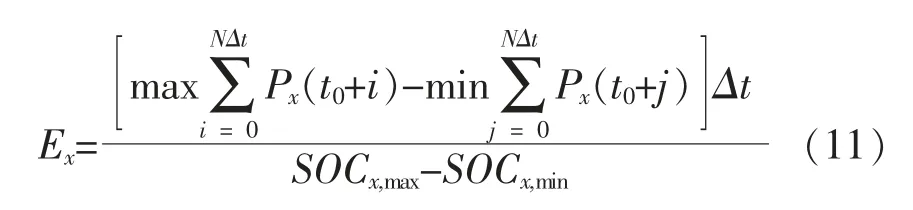
式中：Px（t0+i），Px（t0+j）分别为储能t0+i，t0+j 时刻的功率：N 为时间段总数；SOCx,max，SOCx,min分别为荷电状态的上限、下限。

通过互信息熵重构的初级功率由储能进行承担。在平抑的整个过程中，储能的荷电状态会越过设定的限值， 因此须要采取相应的措施保证荷电状态运行在正常范围。 由于超级电容容量比电池容量小，极易发生越限情况，因此优先调整超级电容的荷电状态，进而调整电池的荷电状态；通过功率限值处理，使储能内部协调优化运行。图3 为自适应调整荷电状态的流程图。

设初始分界点kmi=m，自适应调整分界点经重构分配后的储能功率规则如下：

①若储能的荷电状态都发生越限， 则须要对储能功率进行限值处理；

②若超级电容的荷电状态越限， 则须要减小超级电容的实际出力（即kmi=-1），重新计算荷电状态，并判断是否满足设定的范围；若不满足，则继续较小储能的出力，并对功率进行越限处理，直到满足条件为止；

③由于电池的能量密度比超级电容大， 出现越限的次数少，因此最后对电池的出力进行调整，使其稳定在设定的上下限内。

图3 自适应调整荷电状态的流程图Fig.3 Adaptively adjusting a flow chart of the state of charge

设t 时刻混合储能的调整功率如下：

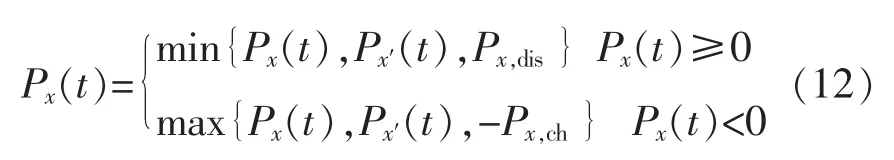
式中：Px′（t） 为t 时刻达到上限或下限时的功率；Px，dis，Px，ch分别为储能的最大充电功率、 放电功率。

不考虑自放电率的情况下， 每一时刻达到上限或下限时的功率：

式中：Ex（t-1）为（t-1）时刻储能装置的剩余容量。

混合储能平抑风电波动的具体步骤如下：

①针对风电功率采用指数平滑法， 将平滑系数进行划分，依次减小平滑系数，直到满足并网标准；

②采用CEEMDAN 对混合储能功率进行分解，得出不同成分的固有模态分量和余量；

③利用互信息理论寻找相邻模态分量混叠最小的分界点，根据分界点重构次高频和高频功率；

④自适应调整分界点， 使储能内部荷电状态运行在稳定范围内。

3 算例分析

以新疆某装机容量为49.5 MW 风电站的实际数据为研究对象， 采用由超级电容器和电池构成的混合储能系统平抑风电波动，采样时间为30 s，采样时长为80 000 s。算例中电池的允许充放电深度为20%～80%，超级电容的允许充放电深度为25%～95%， 初始荷电状态为0.5， 充放电效率为0.95。

根据国家并网波动标准，1 min 和10 min的风电波动分别不大于风电装机容量的1/10和1/3，指数平滑前1 min 和10 min 的风电波动功率为6.18 MW 和19.8 MW。 为满足并网波动要求，平滑系数a=0.16，指数平滑后的波动功率如表1 所示， 风电实际出力和并网功率如图4所示。

表1 风电波动数据Table 1 Fluctuation data of wind power

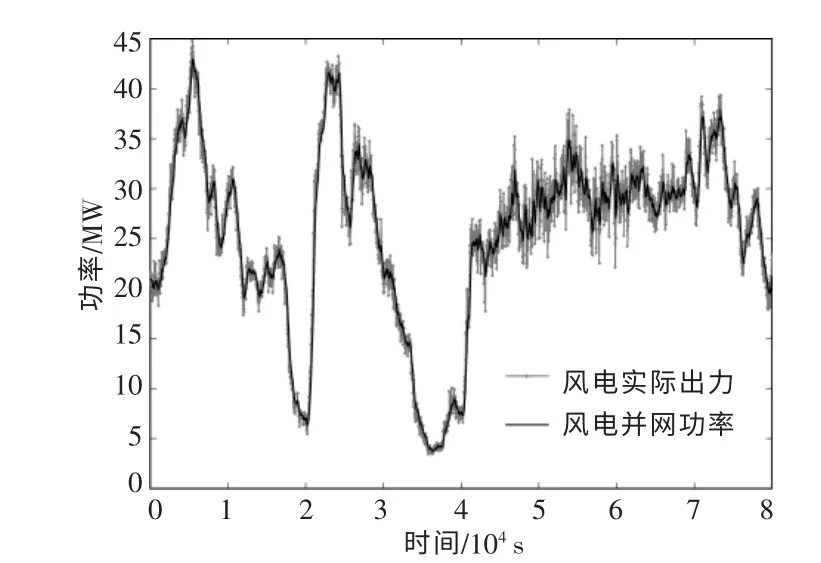
图4 风电实际出力和并网功率Fig.4 Actual power and grid-connected power

采用CEEMDAN 对混合储能功率PHess进行分解，将储能功率分解成11 个IMF 和余量，其分解结果如图5 所示。

图5 混合储能功率经CEEMDAN 分解Fig.5 Hybrid energy storage power is decomposed by CEEMDAN

采用互信息熵方法计算固有模态分量的信息熵。 由表2 所示结果可见，IMF2，3 与IMF3，4 之间的信息熵在递减，而IMF3，4 与IMF4，5 的信息熵在递增。 因此，可以判断kmi=3 为第一个出现的极小值点。 将该点作为次高频分量与高频分量的分界点， 重构得到电池和超级电容所需要平抑的分量，如图6（b）所示，并将EEMD 分解的结果图6（a）与之进行比较。

表2 相邻固有模态之间的互信息Table 2 Mutual information between intrinsic modes

图6 功率曲线Fig.6 Curve of power

图6 （a），（b） 分 别 表 示 经EEMD 方 法 与CEEMDAN 方法分解后重构的初级功率，由超级电容承担波动性较大的高频部分，由电池承担波动性较小的次高频部分。 由图6 可见，采用CEEMDAN方法的电池所承担的功率变化趋势比采用EEMD方法承担的功率变化趋势小，即电池的充放电次数较少；采用CEEMDAN 方法的超级电容输出功率变化区间为[-3.633 MW，3.614 MW]， 采用EEMD 方法的超级电容变化区间为[-8.588 MW，8.861MW]，采用CEEMDAN 方法所需的容量配置较小。

为了避免储能过充过放， 须要对储能功率进行及时调节。 由于超级电容在运行中容易出现剩余容量不足问题，导致储能荷电状态越限较频繁，因此首先对超级电容进行限值处理， 然后再对电池进行调整。 图7 与图8 分别表示经EEMD 与CEEMDAN 分解优化前与优化后的荷电状态。 未调整前，超级电容的荷电状态都出现越限问题，通过减小超级电容的实际出力， 即降低分界点kmi，使荷电状态不越限。 两种方法都能将荷电状态控制在一定的范围。

图7 采用EEMD 方法的混合储能荷电状态Fig.7 Hybrid energy storage state by using EEMD method

图8 采用CEEMDAN 方法的混合储能荷电状态Fig.8 Hybrid energy storage state by using CEEMDAN method

从图7（a）可见，超级电容优化前SOC 范围是[0.137 6，0.973 4]，经过调整回到了[0.25，0.95]。 由图7（b）可见，电池调整前SOC 范围是[0.236 4 0.838 6]，调整后回到了[0.2，0.8]。

从图8（a）见，超级电容未调整前SOC 范围是[0.09，0.97]，经过调整后是[0.253 9，0.938 7]；从图8 （b） 可 见， 电 池 调 整 前 的SOC 范 围 是[0.212 7，0.864 0]，调整后回到了[0.2，0.8]。 由此可知，通过调整分界点，能确保储能的荷电状态控制在合理范围内，提高了储能的使用寿命。

将两种方法分解后的参数对比列于表3。 从表3 的计算结果可以看出，CEEMDAN 分解经重构后，超级电容功率须配置的容量比较小，投资费用也相应较少，且充放电次数约为EEMD 分解重构的一半，延长了使用寿命。 与EEMD 分解重构相比，CEEMDAN 分解重构具有较好的效果。

表3 两种方法分解后参数的对比Table 3 Comparison of decomposition parameters of different methods

4 结束语

本文提出了一种基于指数平滑与CEEMDAN的混合储能控制策略。 采用CEEMDAN 对混合储能功率进行分解，可解决传统EEMD 计算量大的问题，并减小了重构的误差。 由于CEEMDAN 分解获取的固有模态函数能有效克服模态混叠效应， 高、 低频分量的信息能通过互信息真实地反映， 可以用互信息找到重构次高频和高频的临界值。电池吸收波动性较小的低频分量，波动性较大的分量由超级电容吸收。在实际应用中，超级电容配置容量较小，荷电状态容易越限，因此对超级电容优先调整，并根据荷电状态自适应调整分界点，充分发挥出储能不同的响应特性， 确保将储能荷电状态控制在合理范围内。