横向布置单桩潮流能水轮机的数值模拟研究

李东阔， 郑 源， 张 飞， 秦 俊， 邓 磊， 周 攀

（1.国网新源控股有限公司技术中心， 北京 100161； 2.河海大学 创新研究院， 江苏 南京 210098）

0 引言

随着人们对海洋资源的不断开发，潮流能的利用越来越受到重视，作为捕获潮流能的主要装置，潮流能水轮机的应用越来越广泛[1]。 在潮流能水轮机的实际运行过程中，一般采用多台机组运行的方式，而潮流能水轮机在运行过程中会产生尾流，各个机组的尾流会产生相互影响[2]。 因此，多台潮流能水轮机的尾流场与单台潮流能水轮机的尾流场会有所区别。 与此同时，潮流能水轮机的尾流不仅会受到机组设备间尾流的影响，还会受到河床的影响。 在机组间的潮流能水轮机尾流流场的相互影响和融合下， 减小机组间距，能够节约资源，提高机组潮流能水轮机发电场的利用率[3]。 目前，很多专家研究了阻塞效应对单台水轮机尾流的影响，然而，河床和其它机组的限制会改变水流的流态，继而影响尾流的结构，改变尾流与周围流场的混合程度。 多台机组的流速情况和仅受阻塞效应的单个机组运行时有所不同。因此，研究机组间的剪切层对尾流结构的影响以及机组后方的尾流扩张和恢复情况，对于明确后排机组的来流状态是非常重要的。

Chen Y 通过多孔圆盘实验研究单台潮流能水轮机的尾流结构，提出潮流能水轮机的机组性能主要受到来流的影响[4]。 张亚超通过多孔圆盘实验研究了不同初始流速和推力系数对单台潮流能水轮机尾流的影响，结果表明：初始流速越快，尾流收敛越快； 推力系数对尾流的影响集中于水轮机下游5D（D 为水轮机叶轮的直径）范围内，下游15D 以后，推力系数与收敛值无关[5]，[6]。 安佰娜利用水轮机模型进行了流场实验， 得出了水轮机后方尾流流速的恢复规律， 发现布置方式的改变会影响水轮机的水动力特性[7]。Ba i G 通过实验发现，潮流能水轮机的尾流之间会产生相互影响，从而改变尾流的结构，影响尾流发电场的布置[8]。 与此同时，关于机组布置的数值计算研究较少，横向间距对带有单桩支撑结构的潮流能水轮机 （简称为单桩潮流能水轮机） 尾流结构影响规律的研究尚不成熟。

本文以单桩潮流能水轮机为研究对象， 对横向布置的单桩潮流能水轮机模型进行非定常数值计算，研究不同横向间距下，单桩潮流能水轮机模型的机组特性和尾流结构， 为单桩潮流能水轮机的阵列布置研究提供了参考依据， 为潮流能水轮机阵列的优化提供了帮助。

1 计算模型

1.1 单桩潮流能水轮机的基本参数

单桩潮流能水轮机的基本参数如表1 所示。表1 中的来流速度为水槽进口处的流速，转速n为潮流能水轮机的转速。

表1 三维模型的基本参数Table 1 The main parameters of the three-dimensional model

1.2 计算模型的建立

图1 为单排两机组模型的布置图。 图中：x 轴的正方向为水槽的水流流向，y 轴平行于水槽的水平向，z 轴垂直于水槽的底部平面（向上为正方向）。 横向间距Y 为并排两机组转轮中心线之间的距离， 对横向间距分别为2D，2.5D 和3D 时的单桩潮流能水轮机两机组进行三维建模。

图1 单排两机组模型的布置图Fig.1 The model of tidal stream turbine with horizontal arrangement

2 数值计算方法

2.1 CFD 数值计算方法

本文的计算域分为两部分， 即转轮所在的旋转计算域及单桩结构和水槽所构成的静止计算域。 虽然六面体网格在计算精度、变形特性、网格划分数、 抗畸变程度等方面较四面体网格具有明显的优势，但六面体网格不易捕捉复杂的结构。 由于叶片表面的扭曲度较大， 为了保证旋转计算域的计算精度， 旋转计算域采用四面体网格进行划分，并对叶片的前缘、尾缘以及转轮的轮毂部分进行局部网格加密。 静止计算域仅有单桩结构和水槽，模型复杂程度低，因此，静止计算域采用六面体网格进行划分。 计算域的网格划分如图2 所示。

图2 计算域的网格划分Fig.2 Gridding of computing domain

为了确保计算结果不受网格划分的影响，对比分析了相同网格划分方式下， 网格数量对单桩潮流能水轮机的功率系数Cp和推力系数Ct的影响[9]。 不同网格划分的计算为同一工况，湍流模型和边界条件均一致， 来流速度均为0.35 m/s，转速均为66 r/min。 Cp和Ct的计算式为

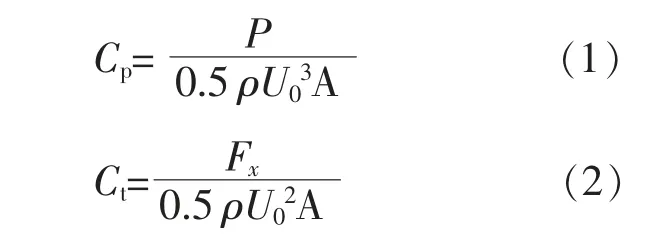
式中：ρ 为水的密度，kg/m3；P 为潮流能水轮机的轴端输出功率，W；Fx为潮流能水轮机的轴向力，N；U0为来流速度，m/s；A 为旋转面的面积，m2。

在横向间距为2D 的情况下，1 号机组的Cp和Ct随网格数量的变化情况如图3 所示。

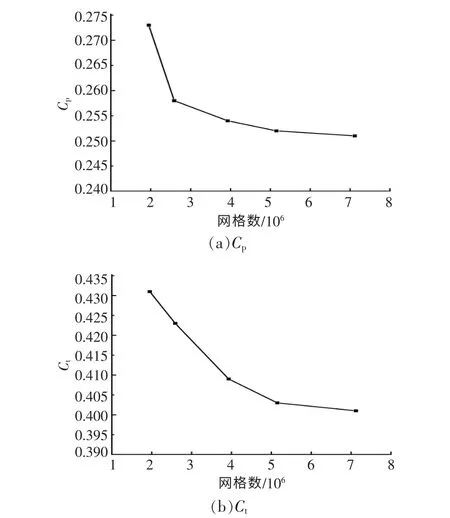
图3 Cp 和Ct随网格数的变化情况Fig.3 Cp and Ctvarying with the number of elements

由图3 可以看出， 随着网格数量的增加，Cp和Ct均先降低，随后数值基本不变。 随着网格数量的增加， 当网格数量达到7.12×106时，Cp和Ct的改变量不超过1%； 当网格数量小于5.15×106时，Cp和Ct的改变量很大， 说明网格数量小于5.15×106时，不利于数值计算的研究。 因此，本文采用的网格数量均为7.12×106， 以确保计算结果不受网格划分的影响。

为了研究水轮机前后水流沿x 方向的分布情况， 对水轮机前后沿x 方向的流速u 进行了量化分析，以u/U0代表相对流速，表示水轮机流场中的水流速度与来流速度的比值。

2.2 边界条件及求解器

王树杰对潮流能水平轴水轮机的湍流模型进行了的研究，发现SST k-ω 湍流模型不仅能够较准确地预测潮流能水轮机的水动力特性，还可以提高数值计算的收敛速度和稳定性[10]~[12]。 因此，本文采用SST k-ω 湍流模型对数值计算进行流动控制。 为了保证数值计算的准确性，在静止计算域中， 水槽的入口边界条件设置为速度入口；出口边界条件设置为自由出流；由于水槽上表面的自由液面对潮流能水轮机的运转影响不大， 为了保证转轮上表面不受壁面剪切力的影响，水槽顶部的边界条件设置为对称面；由于水槽底部会产生速度梯度，水槽下表面的边界条件设置为不可滑移的壁面；水槽两侧壁面的边界条件设置为无滑移的壁面；单桩结构的边界设置为壁面无滑移。

本文不仅考虑了单桩支撑结构对潮流能水轮机的影响， 而且重点研究了潮流能水轮机的尾流效应。因此，本文对单桩潮流能水轮机进行了非定常数值计算，每个时间步长叶片旋转5°，计算时间为15 个叶轮旋转周期。

3 计算结果与分析

3.1 横向布置对机组性能的影响

当来流速度为0.35 m/s， 安装高程为0.27 m时， 单排两机组在不同横向间距下的的功率系数和推力系数如图4 所示。

图4 Cp 和Ct与横向间距的关系Fig.4 Cp and Ct varying with the horizontal spacin

由图4（a）可以看出：在不同横向间距下，两台机组的功率系数基本相同； 当横向间距分别为2D，2.5D 和3D 时，1 号机组的功率系数分 别为0.221，0.215 和0.212，2 号机组的功率系数分别为0.211，0.216 和0.214。 随着横向间距的改变，机组功率系数的变化幅度较小， 在横向间距由2D 增大到3D 的过程中，1 号机组的功率系数的变化幅度不超过0.01，2 号机组的功率系数的变化幅度也不超过0.01。由此可知，横向间距对水轮机的功率系数的影响不明显。

由图4（b）可以看出：在不同横向间距下，两台机组的推力系数基本相同； 当横向间距分别为2D，2.5D 和3D 时，1 号 机 组 的 推 力 系 数 均 为0.351，2 号机组的推力系数分别为0.351，0.361 和0.351。 随着横向间距的改变，机组推力系数的变化较小，在横向间距由2D 增大到3D 的过程中，1号机组的推力系数的变化幅度未超过0.01，2 号机组的推力系数的变化幅度也未超过0.01。 由此可知， 水轮机的推力系数受横向间距变化的影响不大。

3.2 横向布置对水轮机尾流的影响

3.2.1 横向间距对水轮机纵向尾流的影响

当来流速度为0.35 m/s， 安装高程为0.27 m时， 在不同横向间距下， 单排两机组水轮机下游D~8D 内的纵向尾流分布如图5 所示（各分图中，左图为1 号机组，右图为2 号机组）。

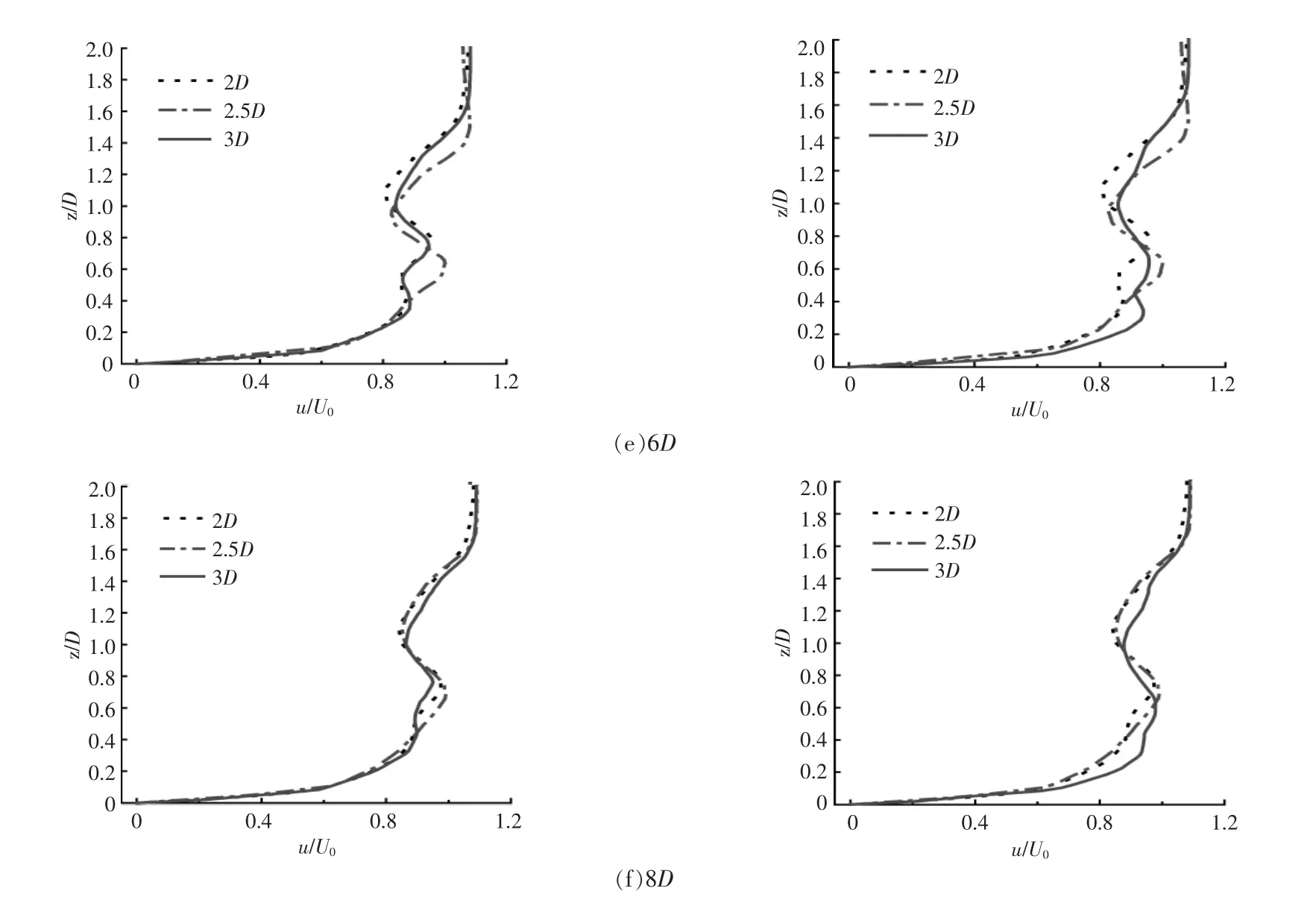
图5 不同横向间距下的纵向尾流分布图Fig.5 Distribution of longitudinal trailing flow with different lateral spacing

由图5 可知， 在水轮机下游的尾流范围内，流速以转轮为中心，呈非对称分布。 产生该现象的主要原因是， 在水槽底部的剪切力作用下，水槽底部附近的流速会产生明显的速度梯度。 此外，由图5（a）可知，在水轮机下游D 位置处，纵向流速具有两个明显的谷值，其中一个谷值位于转轮中心附近 （靠近单桩尾部）， 随着尾流的发展，该谷值不断恢复。 由图5（a）~（e）可知：单桩结构后方有另一处明显的谷值，该谷值位于转轮中心下方，此处的谷值主要是由单桩结构的阻塞作用所造成的；随着尾流的扩展，单桩结构对潮流能水轮机尾流的阻塞作用逐渐减弱，在水轮机后方D~5D 处，该谷值逐渐变大；由图5（e）可知，在水轮机下游5D 处， 该谷值开始消失。 由图5（e）~（f）可知，在水轮机下游5D~8D 处，流速分布情况几乎相似，谷值越来越小，直至没有。由此可知，随着水流的发展，单桩结构的阻塞作用基本消失，这也说明单桩结构会对水轮机的纵向尾流分布产成影响[13]。

由5（a）可知：在水轮机下游D 处，当横向间距分别为2D，2.5D 和3D 时，1 号机组的转轮中心处的流速分别恢复到进口流速的62.3%，71%和73%，2 号机组的转轮中心处的流速分别恢复到进口流速的62%，68%和51%。由此可知，当横向间距相同时，1 号、2 号机组的数值偏差不大；随着横向间距的改变，各机组的转轮后方D 处， 转轮中心位置的尾流恢复程度有所变化， 且随着横向间距的增大， 进口流速恢复变快。

当来流速度和安装高程不变时，1 号、2 号机组的纵向尾流分布相似； 随着横向间距的改变，1号、2 号机组的数值计算结果具有相同的变化趋势；1 号、2 号机组与单台机组的纵向尾流分布大致相同。

3.2.2 横向间距对水轮机横向尾流的影响

当来流速度为0.35 m/s， 安装高程为0.27 m时， 在不同横向间距下， 单排两机组水轮机下游D~8D 内的横向尾流分布如图6 所示 （图中横虚线上部为1 号机组，下部为2 号机组）。 由图6 可以看出：1 号、2 号机组的横向尾流分布相似；随着横向间距的改变，1 号、2 号机组的横向尾流具有相同的变化趋势；1 号、2 号机组与单台机组的横向尾流分布的变化趋势大致相同； 单桩结构对横向尾流的影响很小。

由图6（a）可以看出：随着横向间距的改变，同一断面处，u/U0低于0.9 的范围会发生改变；在水轮机后方D 处，当横向间距分别为2D，2.5D 和3D 时， 两台机组u/U0低于0.9 的范围分别为1.06D，1.15D 和1.32D。 由图6（b）~（f）可知，机组下游2D~8D 处横向尾流具有相同的变化规律。由此可知，在横向尾流中，随着横向间距的增大，u/U0低于0.9 的范围也随之增大。 这是由机组之间的剪切层重叠导致的，间距越大，机组间的剪切层重叠对尾流恢复的影响越小[1]。

图6 不同横向间距横向尾流分布图Fig.6 Transverse wake distribution map with different lateral spacing

1 号、2 号机组尾流的分布基本上和单台机组相似，但是各机组的尾流有些许不对称；与单台机组所不同的是， 横向布置机组的最小速度恢复位置不在转轮中心线方向上，会向Y=0 方向有所偏移。 各机组尾流偏向Y=0 一侧的尾流速度相对于另一侧的尾流流速较低， 这是由机组间的剪切层导致的，因为机组之间的剪切层靠近转轮中心，而水槽边壁的剪切层比较远[1]。 相较而言，机组间的剪切层对机组之间的尾流影响略大， 导致靠近机组剪切层附近的流速恢复变慢。

4 结论

①随着两台机组横向间距的改变， 机组的功率系数和推力系数的变化幅值均不超过0.01，不同横向间距对各机组性能的影响并不明显。

②单桩支撑结构会对水轮机的纵向尾流结构产生影响；横向布置对各机组的尾流无明显影响；横向间距的改变对各机组的尾流也没有明显的影响，但是，在不同横向间距下，尾流的恢复程度会有所变化， 且随着横向间距的增大， 流速恢复变快。

③单桩支撑结构对水轮机的横向尾流结构影响较小； 各机组尾流最小速度的恢复位置向Y=0方向有所偏移； 随着横向间距的增大， 两台机组u/U0低于0.9 的范围随之增大，幅值可达0.26D。