无位置传感器伺服系统分数阶滑模观测器设计

聂智博，赵志诚，高慧敏

(1.太原科技大学 电子信息工程学院，太原 030024；2.嘉兴学院 机电工程学院，浙江 嘉兴 314000)

由于信息化时代的到来，现代战争对我军联合作战能力提出了极大的挑战，相应的对武器装备的精准迅速提出了要求，光电伺服跟踪系统作为现代武器的重要组成部分，因此也对其提出了很高要求。永磁同步电机(Permanent Magnet Synchronous Motor，PMSM)具有体积小、功率密度高、转动惯量低、高效节能等优点[1]，被广泛应用在光电跟踪系统中。传统的PMSM光电伺服跟踪系统，通常在转子上安装旋变来方便获取转子速度，但是这会增加系统的复杂度和成本，降低系统的可靠性，使其在实际应用中受到一定的限制。因此，把无传感器控制技术应用在PMSM光电伺服跟踪系统中已经成为了一种趋势。

目前无速度传感器的研究方法有：高频注入法[2]、模型参考自适应法[3]、扩展卡尔曼滤波器法[4]、滑模观测器法[5-6]、神经网络[7]等。其中滑模观测器方法有诸多优点，为此在实际中得到广泛应用，但是，滑模变结构的一大弊病是存在着明显抖振，为此学者们开展了一系列的研究。文献[8]通过引入高阶滑模来减小系统抖振和提高系统观测精度，仿真结果表明该设计方法具有可行性。文献[9-12]分别采用一些连续光滑的曲线来代替开关函数，在一定程度上抑制了系统抖振，提高了观测精度。

考虑到分数阶微积分具有记忆、鲁棒性强等特征，本文在非奇异终端滑模面上引入分数阶微积分算子，通过分数阶控制律得到连续光滑的反电动势估算值，最后，通过分数阶锁相环精确估算出电机转速。经仿真验证，将分数阶模型应用在滑模观测器中可实现控制方式间的平滑切换，有效减小了系统抖振，提高了对转速的估算精度。

1 传统滑模观测器设计

PMSM两相静止坐标的数学模型：

(1)

式中：is=[iα，iβ]T，us=[uα，uβ]T，iα，iβ，uα，uβ分别为α，β轴的定子电流(A)与电压(V)；eα，eβ为α，β轴的反电动势(V)；L，Rs为定子等效电感(H)与电阻(Ω)；ψf为磁链(WB)；ωr,θr为电机转子速度(r/min)与转子角度(rad)。

根据式(1)构造传统设计方法的状态方程：

(2)

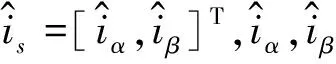
式(2)减去式(1)可以得到：

(3)

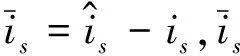
(4)

(5)

由式(5)可知反电动势存在不连续信号，需要滤除高频切换信号，得到估算反电势为：

(6)

因为引用了一个低通滤波器，会引发相位延迟，所以需要额外加一个角度，进行相位补偿：

(7)

(8)

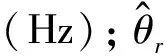
2 分数阶非奇异终端滑模观测器设计

本文提出一种分数阶非奇异终端滑模观测器设计方法，来提高传统滑模观测器对转子的估算精度，实现对电机转子位置与转速的准确、快速估计。

重新构建滑模观测器如下：

(9)

式(9)减去式(1)得到电流误差方程：

(10)

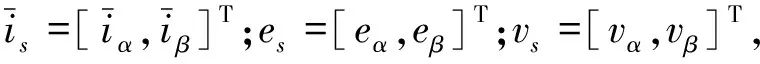
(11)

(12)

为实现对外部噪声和系统参数变化的鲁棒控制，设计控制率如下：

ν=νn+νeq

(13)

(14)

(k+η)sgns+μs]

(15)

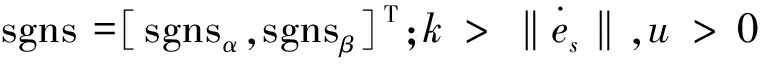
设Lyapunov函数为：

在对函数求导前，先把控制率v带入电流误差函数得到：

(16)

并对该函数求导：

(17)

对Lyapunov函数求导：

(18)

将公式vn代入公式(18)得出：

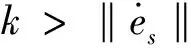
(19)

3 基于分数阶锁相环的转速估算

传统滑模观测器通常先进行相位补偿，得到相位角，然后对其求导得到转速。但是有两点不足：第一，微分环节的引入会导致抖振，第二，需要制作相位补偿角度表。本文结合分数阶PID控制鲁棒性强和锁相环相频跟踪好的特点，使用分数阶锁相环(Fractional order phase-locked loop，FO-PLL)来估算转子位置和转速，分数阶锁相环结构图如图1所示。

对图1算法进行分析：

(20)

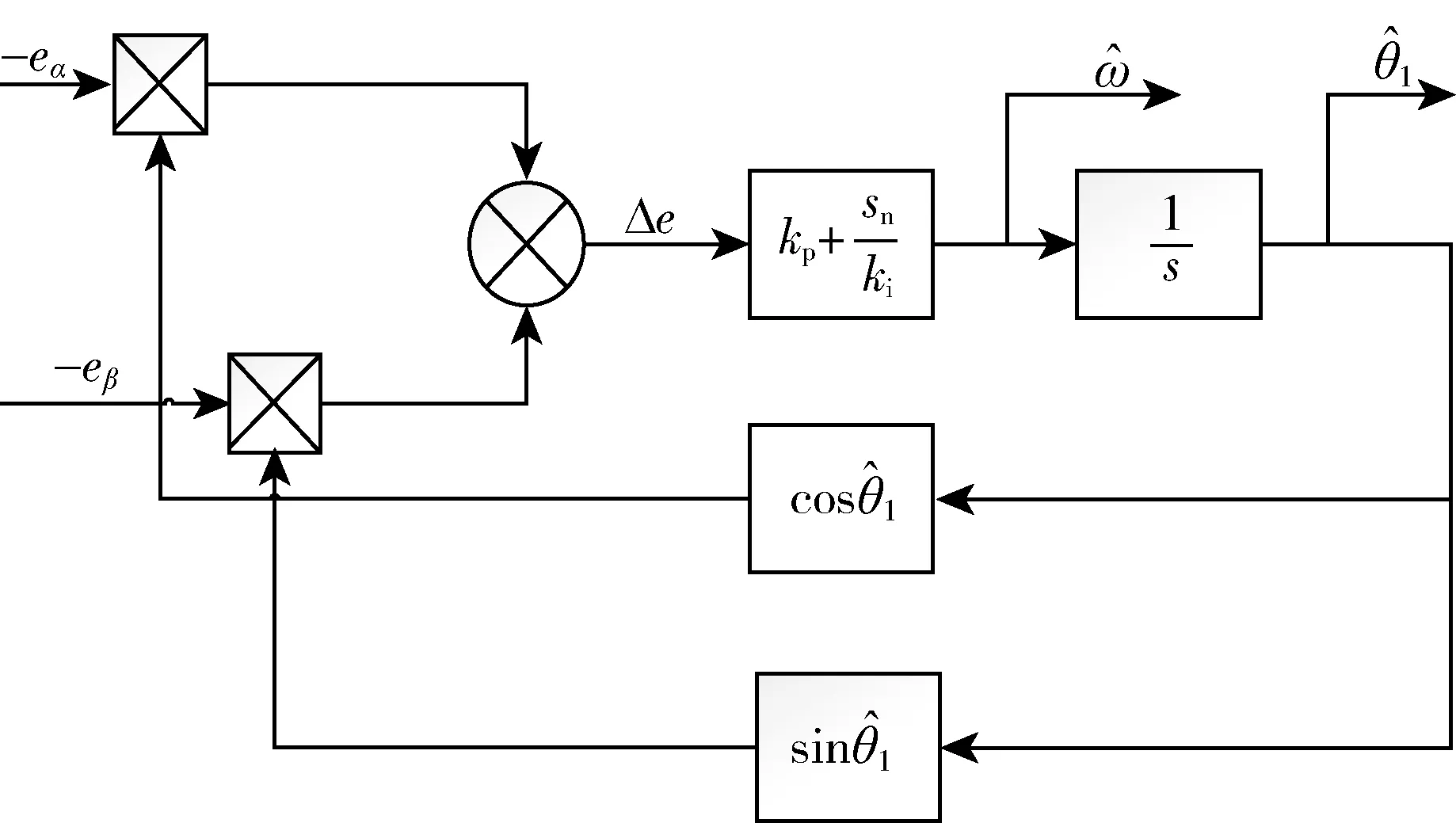
图1 分数阶锁相环结构框图

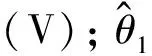
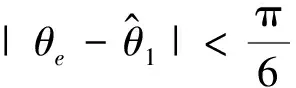
(21)

锁相环闭环传递函数为：

(22)

锁相环误差传递函数为：

(23)

系统的稳态误差：

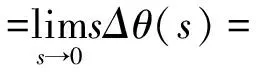
(24)

4 仿真验证与分析

在MATLAB/Simulink平台上建立基于PMSM的分数阶滑模观测器仿真模型，采用id=0的矢量控制策略，实现对永磁同步电机的无传感器控制，控制系统框图如图2所示。

仿真所采用的电机额定参数为：

UN=220 V，R=2.875 0 Ω，L=8.5e-3H，ψf=0.175 Wb，J=e-3kg·m2，极对数p=4.

本文设计方法的参数为：q=3，p=5，γ=0.001，c=1，u=0.8，μ=1 200，k=20 000，η=400，r=0.85，kp=20，ki=500.

传统设计方法的参数为：

k=200，wc=20 000.

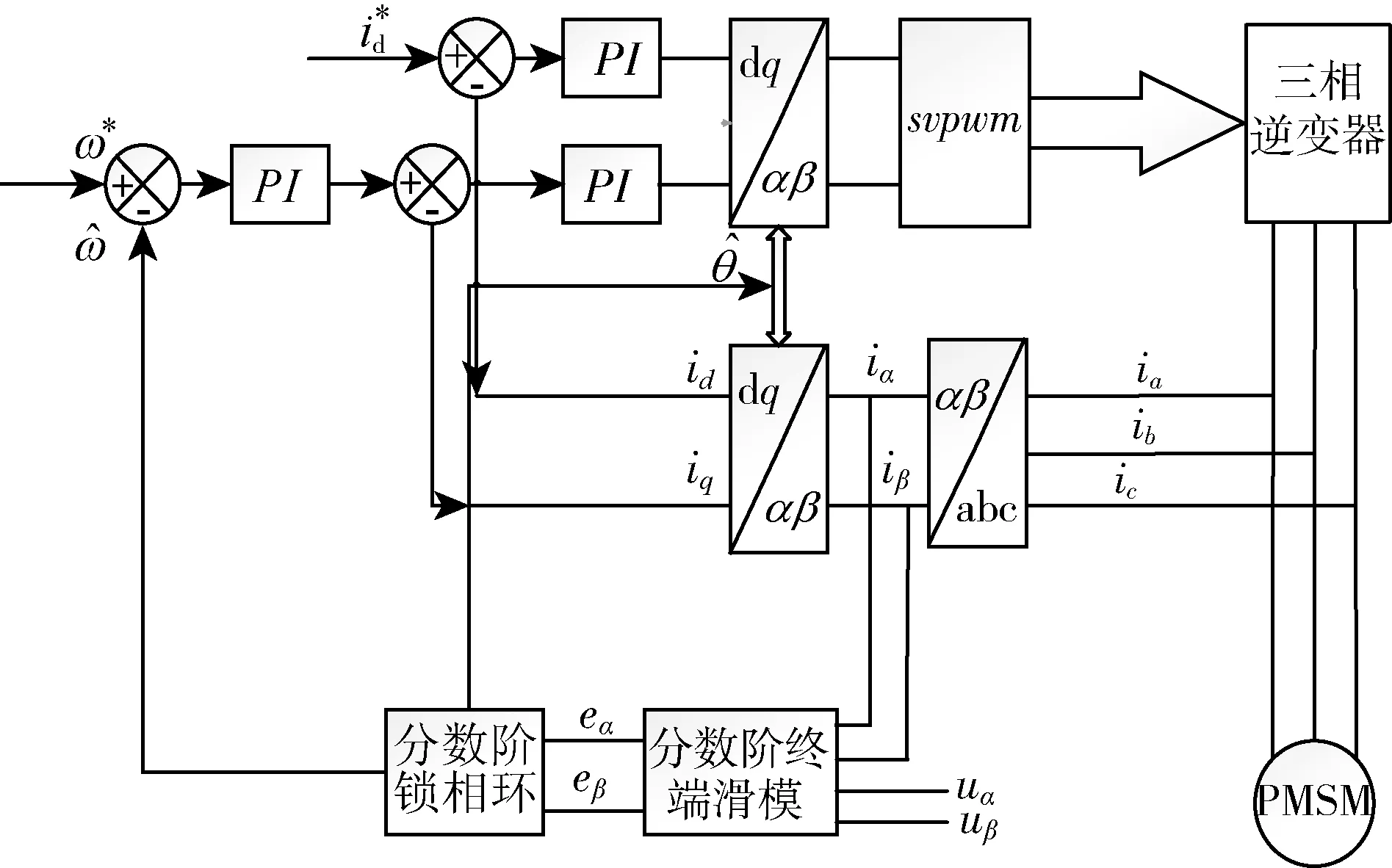
图2 控制系统框图

当系统速度设置为1 000 r/min时，图3，5是使用传统方法的系统仿真结果，图4，6是使用本文设计方法的系统仿真结果。

从图3(a)可见，当使用传统设计方法来估算转速时，估算出来的速度波动很大，并且存在大量的高次谐波。从图3(b)可看出在低速时转速估算误差接近18 r/min，在高速时转速估算误差接近12 r/min，从而可以得出结论：当系统使用传统设计方法时，在低速时转速估算误差最大，转速估算精度较低，使其在实际应用中受到一定限制，高速时转速估算误差较低速时有所减小，但是还是难以满足实际要求。

从图4(a)可以看出，系统采用本文提出的设计方法时，对转速的估算波动小，曲线光滑，不存在高次谐波，估算精度较高。从图4(b)看出，在低速时转子速度的估算误差小于10 r/min，高速时转子速度的估算误差小于1 r/min，可以看出本文提出的滑模观测器设计方法无论在低速，还是高速都可以实现对转速的精准跟踪，满足实际应用的基本要求。从图5(a)，(b)，图6(a)，(b)可以看出，传统设计方法虽然补偿了相位，但是对转子位置的估计仍存在滞后，使其在实际应用中受到限制。本文提出的设计方法，使用分数阶锁相环估计转子位置，估算出来的转子位置能够与实际转子位置几乎保持一致。

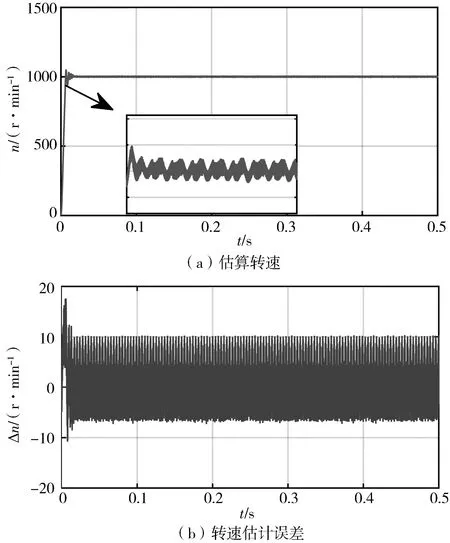
图3 传统滑模观测器转速分析

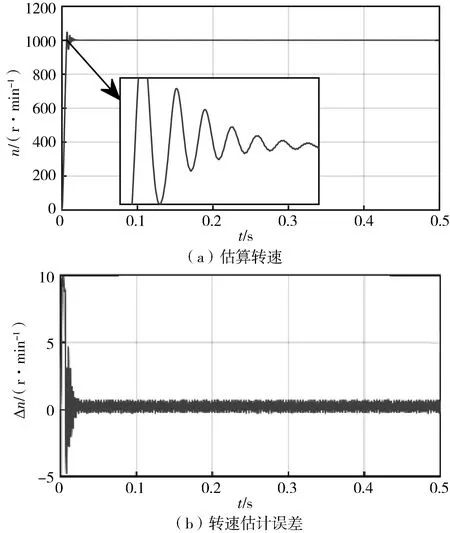
图4 分数阶非奇异终端滑模观测器转速分析

图5 传统滑模观测器转子位置分析

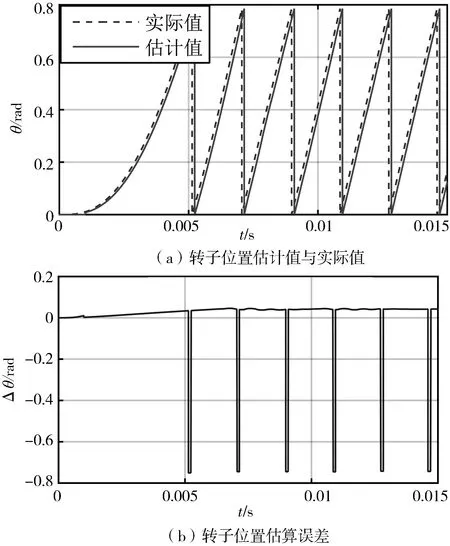
图6 分数阶非奇异终端滑模观测器转子位置分析

为验证本文所提方法在转速发生突变时，能否精准跟踪转速。当系统初始速度是800 r/min时，在0.2 s时转速突然变成1 000 r/min情况时，图7是系统使用传统设计方法的仿真结果，图8是系统使用本文设计方法的仿真结果。

从图7(a)，(b)可以看出，当在0.2 s改变转速，系统使用传统设计方法时，对转子速度的估算偏差超过14 r/min，0.04 s以后对转子速度的估算偏差减小到9 r/min，但是还是无法精准、快速跟踪转速。从图8(a)，(b)可见，当在0.2 s转子速度突然发生变化时，系统使用本文设计方法时，对转子速度的估计偏差小于8 r/min，0.02 s以后对转子速度的估计偏差小于2 r/min，可以看出当转子速度突然发生变化时，本文所提方法可以快速跟踪实际转速并且估算偏差很小。

5 结论

为了提高光电伺服跟踪系统对转速的估算精度，本文设计了分数阶非奇异终端滑模观测器，提出的控制律中不仅有积分项还有分数阶项，可以很好的对信号进行滤波处理。然后，通过分数阶锁相环调制出转子速度，所以分数阶滑模观测器不需要加滤波器，也不需要加角度补偿，就可以提高观测器估算精度，减小系统抖振，克服传统滑模观测器存在的相位滞后与高频抖振现象。仿真结果表明，本文提出的设计方法能实时的跟踪转子位置与转速，有效减小了系统抖振，提高了对转速的估算精度。

图7 传统滑模观测器转速突变分析

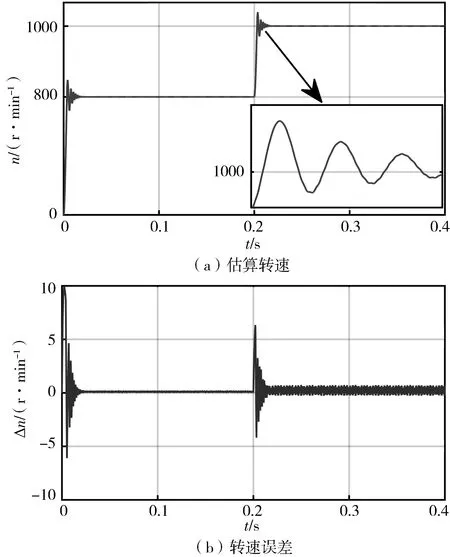
图8 分数阶非奇异终端滑模观测器转速突变分析