基于灰色预测模型对桥梁技术状况预测的研究

杨文博，韩智强，贾志绚

(太原科技大学 交通与物流学院，太原 030024)

目前,我国公路桥梁已经超过80万座，但由于例如环境、交通流量、桥梁结构与类型、设计与施工、养护与管理等内在和外在各种因素的互相作用，使得桥梁的技术状况随时间推移而逐步退化，不仅影响桥梁的正常使用，严重的更危及使用者的生命安全，所以开展桥梁技术状况预测与评定具有重要的现实意义。

多数的发达国家在桥梁管理方面所做的工作已经足够完善，譬如美国的国家桥梁数据库，早在20世纪70年代就已经建立，并在二十多年前由美国国有公路运输管理员协会开发成了桥梁管理系统Potins.此系统先将桥梁构件按材料特性分类，然后分析不同类型构件退化的因素并得出对退化趋势的预测。欧美和日本的许多公司进行技术状况预测的方法都是马尔可夫模型预测法，并且由于已使用多年，这些桥梁管理系统都已经比较成熟[1]。

在国内，马军海等[2]确定桥梁技术状况等级的方法是，将之分为功能性技术状况、易损性技术状况、损伤性技术状况三个体系再进行量化评定。但论文没有具体说明技术状况与养护管理的相关性，也没有建立具体的决策模型。耿波等[3]使用马尔可夫预测法建立模型，并对此模型进行研究。但是其模型实质仍是利用指数函数拟合原始数据，与回归分析模型结果相似，并且受原始数据的波动性影响较大。陈雅琴[4]进行了少数据量状况下的灰色系统理论对于桥梁技术状况的预测。常健等[5]借助层次分析法，结合权重指标建立桥梁安全性评价模型以得到该桥梁安全性评价等级，并通过一拱桥案例说明其可行性。

在国外，Jiang和sinha[6]建立了动态马尔可夫模型以预测印第安纳州桥梁的缺损状况。Cesare等[7]通过桥梁状态数据库中的资料构建静态马尔可夫模型，并预测纽约地区混凝土桥梁面板缺损状况。Sobanjo[8]将多层人工神经网络与桥梁的桥龄、上部结构的等级联系到一起。Tokdemir等[9]做了基于事例推理(Case-based Reasoning)的研究，是近些年预测桥梁退化趋势的新方法。

针对桥梁的状态预测，应采用适当的数学模型作为预测方法，并将历年桥梁评估结果作为原始数据序列。现有的各类预测方法非常多，而通常用于桥梁技术状况的方法主要有马尔可夫预测、回归分析法、趋势外推法、齐次泊松过程模型、残差辩识法、德尔菲法、指数平滑线法和灰色预测法等[10]。

1 灰色系统简介

灰色系统理论诞生于1982年，由邓聚龙在北荷兰出版的一篇题为“control problem of grey systems”的论文中首次提出[11]，这是一种研究少数据、贫信息以及不确定性问题的方法。主要原理是借助对“己知部分信息”的挖掘和研究，进一步去实现对系统行为特征、演化规律的正确描述和有效监控。灰色系统模型对实测数据没有什么特殊的要求和限制，因而有着十分广阔的发展前景。

灰色系统理论主要包含三个模块：数据采集、灰色建模和灰色预测。灰色建模是在灰色数据生成基础上，建立近似微分方程，n阶、h个变量的模型GM(n，h).其中把GM(1,1)模型作为灰色预测的基础，面向事物的发展趋势与状态进行预测。

由于桥梁工作状态的特殊性，其整个变化的过程相当缓慢，若每次评估时间间隔较短，则其结果无法充分反映桥梁状态变化的趋势。故应以年为时间单位，进行年度综合桥梁评估，方能得到较为理想的基础数据，也就是预测所需的灰信息。因此本文将以某运营桥梁为依托工程，采集四年间技术状况评分的原始数据，进而以灰色理论方法进行建模，并预测桥梁的后续运营状况。

2 GM(1,1)模型建立与检验

灰色系统模型建立的具体流程图如图1所示。

图1 灰色理论分析流程图

2.1 GM(1,1)模型建立[12]

(1)级比检验

建模前应对原始序列x(0)作可行性检验，检验方法为：对原始序列x(0)={x(0)(1)，x(0)(2)，…，x(0)(n)}，计算级比：

得级比数列σ(0)={σ(0)(1),σ(0)(2),…，σ(0)(n)}，

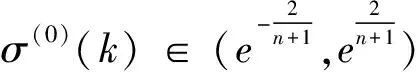
例如n=4时，σ(0)∈(0.67,1.49)，则认为x(0)是可做GM(1，1)建模的。

(2)灰色模型生成

将时间序列Χ(0)=(x(0)(1),x(0)(2),x(0)(3),…,x(n)(n))进行累加生成。

设x(0)为GM(1，1)建模序列

x(0)={x(0)(1),x(0)(2),…，x(0)(n)}

x(0)的AGO(累加生成)序列x(1)为：

x(1)={x(1)(1),x(1)(2),…，x(1)(n)}

(3)生成紧邻均值序列

构建基于Χ(1)的背景值序Ζ(1)=(z(1)(1)，z(1)(2)，…，z(1)(k))其中z(k+1)=0.5x(1)(k)+0.5x(1)(k-1)，k=1,2,…,n-1

(4)建立GM(1,1)模型

x(1)序列的均值(MEAN)序列z(1)为：

z(1)={z(1)(1),z(1)(2),…，z(1)(n)}

其中：z(1)(k)=0.5x(1)(k)+0.5x(1)(k-1)

则GM(1，1)模型的灰微分方程为：

x(0)(k)+az(1)(k)=b

将k=2,3,…，n代入上式，有:

将上述方程组转化为矩阵方程：

yN=BP

其中：yN=[x(0)(2),x(0)(3),…，x(0)(n)]

2.2 GM(1,1)模型精度检验

(1)模型精度检验

因为选取的原始序列为小样本数据，所以应采用比较直观的残差大小检验法来进行模型的精度检验，只有精度满足要求的模型才能正常使用。

令ε(k)为残差相对误差

p0为精度，其定义为：p0=(1-ε(avg))100%

(2)预测

白化方程的时间响应序列为:

k=1,2,…n

k=1,2,…n

3 工程实例分析

3.1 数据采集

本文以某运营桥梁为例，统计其2013年-2016年技术状况评分，如表1所示，评分标准采用《公路桥梁技术状况评定标准》(JTG/THZ1-2011)[13].

表1 桥梁技术状况评分

Tab.1 Bridge technical status score

年份评分2013100201497.42201593.38201687.50

3.2 数据分析

(1)初始化建模原始序列

(100,97.42,93.38,87.50)

(2)原始序列的1-AGO生成

Χ(0)的1-AGO生成序列Χ(1):

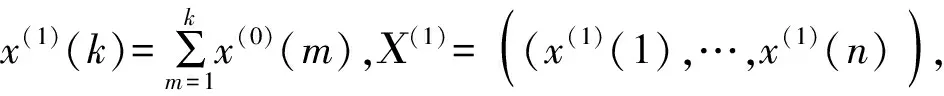
对Χ(0)进行准光滑性检验：

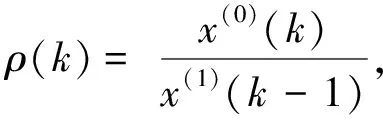
检验Χ(1)是否具有准指数规律：

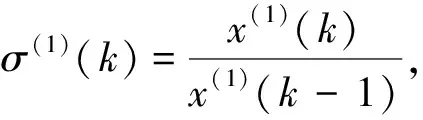
(3)1-AGO生成序列的紧邻均值生成

对Χ(1)作紧邻均值生成Ζ(1)

z(1)(k)=0.5x(1)(k)+0.5x(1)(k-1)，k=2,3,4

(4)计算灰色模型发展系数a和灰色作用量b，求得模拟值

a=0.053，b=105.684

确定GM(1，1)模型

dx(1)/dt+0.05266x(1)=105.684

以及时间响应式

求X(1)的模拟值:

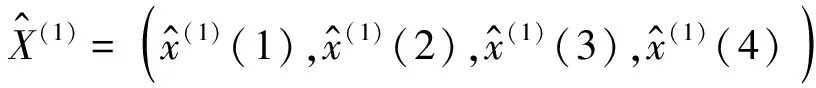
还原求出Χ(0)的模拟值:

3.3 检验误差

表2 误差检验表

Tab.2 Error check list

序号实际数据模拟数据残差相对模拟误差/%297.42097.730 -0.3100.318393.38092.6590.7210.772487.50087.852-0.3520.402

0.998>0.90，

由表3可知关联度为一级。

计算均方差比C：

计算小误差概率：0.6745S1=3.182

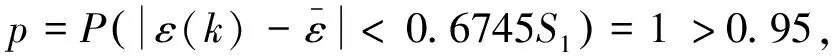
3.4 预测分析

表3 模型检验分类表[14]

Tab.3 Model test classificationlist

相对误差ε(k)/%关联度γ均方差比值C小误差概率P一级10.900.350.95二级50.800.500.80三级100.700.650.70四级200.600.800.60

通过表3 进行模型精度检验可知，相对误差、关联度、均方差比值与小误差概率这些指标全部满足一级精度要求，并做图2 灰色预测模拟值与实测数据对比图。

图2 灰色预测模拟值与实测数据对比图

从图2可以看到灰色预测模型与原始数据拟合情况较好，因此采用灰色预测GM(1，1)模型对桥梁进行技术状况预测可以得到较为准确的结果。

因此可用下式进行预测。

这里给出4个预测值为：

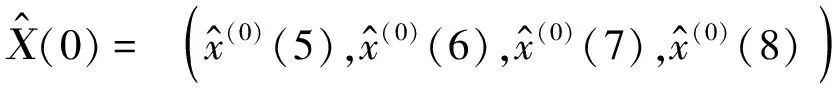
可得出结果：按目前的变化趋势，今后4年该桥梁状态评估预测为83.294，78.972，74.875，70.990.

4 结 论

本文主要介绍了灰色预测理论在桥梁评估的应用，着重介绍了灰色预测GM(1，1)的建模流程，并对建模数据进行相对误差、关联度、均方差比值、小误差概率的检验，并以某运营桥梁为为例，进行建模分析，其结果均能满足相关精度要求，并起到较好的效果，其研究成果可为桥梁运营状态评估提供参考。