基于灰色极限学习机组合光伏发电预测

苗言明,刘立群,王 伟,刘春霞

(太原科技大学电子信息工程学院,太原 030024)

随着光伏发电技术的快速发展，光伏发电成为当前能源供给重要来源。在建立光伏发电系统时，由于系统输出功率的需要，需要满足多个外部环境因素才能正常运作，例如光照、温度等，随着外部因素的改变，光伏发电系统输出功率将产生波动，影响系统整体的稳定性，对发电质量产生直接影响。随着光伏发电系统渗透率的提升，系统在复杂程度、风险性方面也会上升。所以，通过准确评估光伏发电输出功率相关问题，能帮助电力调度部门进行合理的风险规划，制定严谨的计划，以此提升电力系统的安全系数，使光伏发电建立竞争壁垒[1]。光伏发电属于间歇性较为显著的能源，给智能电网带来了巨大的波动性，给系统稳定性、电力调度、无功补偿和频率响应等方面带来了严峻的挑战。为了改善这种情况，有必要对输出功率进行预测[2]。光伏输出与负荷预测有利于国网预知可再生能源发电和负荷消耗的准确预测信息，保证供需侧始终保持平衡，降低运行储备的容量和成本。由于光伏发电功率预测是一个非线性的随机问题，所以关于“向量机”“极限学习机”“神经网络”德国智能算法有更多的应用。

AbdollahKavousi-Fard[3]通过结合“支持向量回归模型”“ARIMA”“布谷鸟搜索算法”等算法，以全新的组合预测方式验证2009年法尔斯电力公司伊朗电力消耗状况，并总结真实的数据。结果显示：组合预测方法比单一算法作用效果更显著，在精准度、时效性等方面更为优秀。李芬[4]提出一种基于灰色关联分析(GRA)结合BP神经网络(GRA—BPNN)的变权重系数组合预测模型，分析结果表明：GRA—BPNN变权重组合预测模型相对均方根与相对平均存在的误差与单一模型、等权重组合模型相比要高。吴婕[5]等人以多项式系数自回归(PCAR)模型为基础，采用基于奇异值分解滤波算法的联合PACA的组合模型，实验表明组合预测要比单一自回归滑动平均模型(ARMA)预测准确值高。王守相[6]等提出一种以灰色神经网络组合模型为基础的光伏出力预测方法，通过三种模型的结合，并分别比较预测结果。研究结果表明，灰色神经网络组合模型在分析和预测光伏出力时精准度最高。李芬[7]等以IOWA算子为基础，综合利用误差平方、最小为准则建立优化模型，充分考虑不同预测模型的优势，设计短期光伏发电量相关预测模型。在针对“华中科技大学研究中心18 kW并网光伏电站”分析资料表明：预测模型是降低结果误差的关键，有利于精准度的提升。李多[8]等通过结合EMD、ELM两种预测方法，并形成全新的预测模型,可对不同分量值进行判断；最后使用ELM判断不同分量值之间的和，最终满足预测需要。通过上述案例，该方法显然比传统预测方法更为优秀，在准确度方面的优势尤为明显。

基于以上分析，针对性提出以灰色极限学习机组合模型为基础的电力预测方式，通过极限学习机、灰色预测相互配合，从而融合了两者的优点，弥补了各自的不足之处。选取某光伏发电机组2019年3、4月发电量进行建模预测，验证所建立的预测模型准确度。

1 模型方法

1.1 灰色GM(1，1)

1.1.1 基本概念

灰色预测是指以灰色系统理论为基础的预测，通过系统因素分析，研究不同因素发展变化的差异程度，并分析不同的关联因素，对原始数据进行处理，观察其中的规律，归纳有效数据序列。最后，通过形成一阶微分方程模型[9]。灰色预测模型对原始数据标准较低，并且无需根据特征量计算，同时也无需考虑分布是否规律。

1.1.2 GM(1,1)模型的建立

(1)假设X(0)=原始序列，n=数据个数。

X(0)=[x(0)(1),x(0)(2),x(0)(3),…,x(0)(n)]，

∀x(0)(i)∈R+，n∈N

(1)

(2)对X(0)累加得到新的序列式

X(1)=[x(1)(1),x(1)(2),x(1)(3),…,x(1)(n)]

(2)

其中

称X(1)为X(0)的一次累加生成，记为1-AGO.

(3)设X(0)为原始序列，n为数据个数。

X(0)=[x(0)(1),x(0)(2),x(0)(3),…,x(0)(n)],

∀x(0)(i)∈R+，n∈N

(3)

α(1)X(0)=[α(1)x(0)(1),α(1)x(0)(2),

α(1)x(0)(3),…,α(1)x(0)(n)]

(4)

其中α(1)X(0)=X(0)(k)-X(0)(k-1)，k=1,2,…,n.称α(1)X(0)为X(0)的一次累减生成。

(4)生成X(1)的邻均值等权数列如式：

z(1)=(z(1)(2),z(1)(3),…,z(1)(k)),

k=2,3,…,n

(5)

(5)以灰色预测为基础，分析x(1)关于t一元一阶微分方程，具体如下式：

(6)

其中，a,u——待解系数(发展系数、灰色作用量)，记a，u分别为矩阵灰参数，如下：

(7)

(6)均值处理后的累加序列可计作B，B与Y(n)的关系式如下所示:

(8)

(7)利用最小二乘法分析灰色参数，公式如下：

=(BTB)-1BTYn

(9)

(10)

(8)建立原始序列模型，如下式所示：

k=1,2，…，n-1,

(11)

1.2 极限学习机模型的建立

1.2.1 基本概念

早前Haung[10]等人提出关于极限学习机的概念，其是一种简单高效的勇于评估单隐层前馈神经网络的分析手法，ELM属于新的单隐层前馈神经网络。ELM是具有代表性的，可随机输入隐层神经元的权值与阈值矩阵，随后，通过最小二乘法的方式评估对应的权值[11].在算法中，随机选取网络输入权值、隐层偏置是最核心的部分，并且保持训练过程的不变，则需要对隐层神经元个数进行调整和优化。网络输出权值基于最小化平方损失函数分析Moore Penrose广义逆运算，并可得最小二乘解。与其他传统梯度前馈神经网络学习算法相比，ELM操作简单、容易上手，并且可忽略认为干预因素的影响，整体优势非常显著[12]，ELM是目前人工智能领域应用最多，使用最为广泛的方法之一。

1.2.2 极限学习机模型的建立

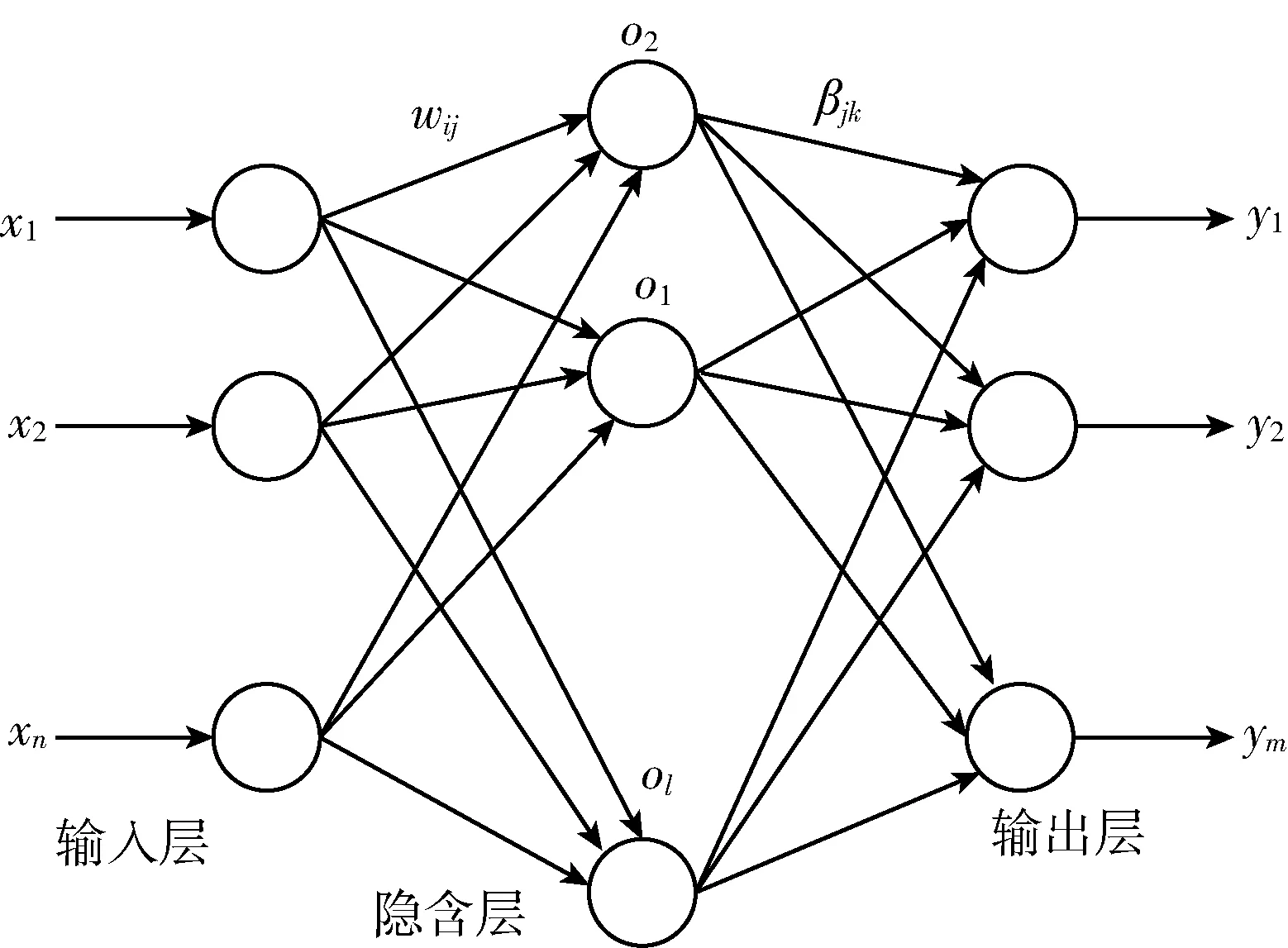
图1 单隐层前馈神经网络结构

其中，输入层和输出层分别存在n个和m个神经元，其对应n个输入变量、m个输出变量，假设隐含层、输入层连接权值矩阵计作“w”，可用如下公式表示:

(12)

其中，输入层第j个神经元、隐含层第i个神经元之间的连接权值可用ωij表示。

假设输出层、隐含层连接权值计作“β”，即可用如下公式表示：

(13)

其中，输出层第k个神经元、隐含层第j个神经元间连接权值可用βjk表示。假设隐含层神经元阈值为“b”，则有如下公式：

(14)

假设存在M个样本可作为训练数据，并且可用作矩阵X与矩阵Y的数据，具体公式如下所示：

(15)

(16)

假设隐含层神经元激活函数记作“g(x)”，那么网络输出T可用下面公式表示:

(j=1,2,…Q)

(17)

其中：ωi=[ωi1ωi2…ωin]，xj=[x1jx2j…xnj]T

上式可表示为：Hβ=TT

H=

(18)

2 灰色极限学习机组合模型合预测

“灰色预测算法”“极限学习机算法”两个预测模块共同组成灰色极限学习机预测算法，改算法可满足小量样本的数据检测，当样本数量较多时，灰色预测模型比数据建模预测效果要差。一般情况下，在面对大样本数据预测时会有效考虑极限学习机的方法，并且随着样本数据增加，预测整体拟合度更强，整体误差也会越低。所以，在使用灰色极限学习机预测算法时，可以在样本收集前选取少量样本进行建模测量，并通过分析不同的样本数据利用极限学习机进行分析，随后通过不同模型分别对样本进行测量，分别对测量结果进行加权处理，随后以求和的方式分析最终的测量结果[13]。

2.1 组合预测模型的构建

在关于开展某个项目的预测时，可首先收集整理相关数据，并计作“Y”，表达式为：Y=(y1,y2,…,yn)，选取m个单项预测模型进行评估，并建立相关模型，即{φ1,φ2，…,φm},当处于第t(t=1，2，…，n)时刻预测值个表示为{φ1(t),φ2(t),…,φm(t)}。

假设权重向量表达式：

λ=(λ1,λ2,…,λm)

φ(t)=λ1φ1(t)+λ2φ2(t)+…+λmφm(t)=

(19)

本文以MAPE为基础，明确权重系数相关模型，具体表达公式如下所示：

t=1,2,…,n

(20)

遵循原则就是MAPE模型在整个组合模型体系中权重偏低[14]，假设“m”个单向模型(MAPE)是d1,d2,..dm,d，那么第i个模型的权重系数可表示为：

(21)

用此种方法构造的组合预测模型的表达式为：

φ(1)(t)=a1φ1(t)+a2φ2(t)+…+amφm(t)=

(22)

选取某光伏发电机组2019年3、4月发电量进行建模预测，其中，随机抽取50个发电量样本当作训练数据，并选择其中的10天数据进行预测，对灰色极限学习机组合模型的精度进行验证。3种模型的预测结果和实测值数据见表1，对比见图2：

表1 3种模型的预测结果和实测值数据

Tab.1 Prediction results and measured data of the three models

实际值(w)灰色模型预测值(W)Grey 绝对误差%极限学习机预测值(W)绝对误差/%灰色极限学习机组合预测值(W)绝对误差/%398.12398.120389.978.15394.953.17399.45399.050.4402.963.51400.571.12403.74411.888.14399.174.57406.943.2427.96425.132.83431.693.73427.680.28429.08438.809.72421.837.25432.23.12460.91452.918464.964.05457.63.31472.80467.485.32477.744.94471.471.33497.45482.5114.94506.619.16491.885.57498.60498.030.57499.721.12498.690.09499.95514.0414.09491.798.16505.385.43

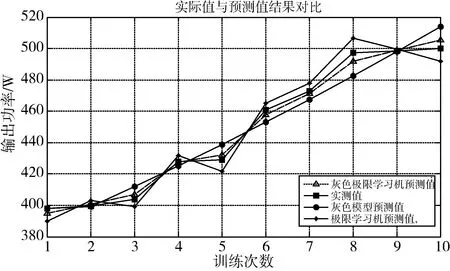
图2 3种模型的预测结果和实测值对比图

由上述图表可以得出，灰色极限学习机组合模型的预测结果比较理想，其预测值能够较好地拟合功率变化的趋势，逼近真实值。经计算得出灰色GM(1，1)模型的平均相对误差是1.925%，极限学习机的平均相对误差是1.224%，而经过MAPE加权组合预测的平均相对误差是0.59%，预测精度明显提高。

3 结论

根据某光伏电站3、4月份发电量数据，分别对灰色GM(1，1)模型、极限学习机模型进行了预测，通过MAPE的大小分配权重并重新组合建立了灰色极限学习机组合模型，根据数据解算表明:三种模型均可满足发电功率预测精度的标准，三种模型分析误差别分别极限学习机1.224%、GM(1，1)模型1.925%、组合模型0.59%，可见组合模型整体误差程度最低。并且通过灰色极限学习组合的方法，能分配不同预测模型的权重，发挥不同模型的特长，以此实现更高质量的预测效果。