分数Maxwell黏弹性胶体阻尼缓冲器振荡流模型研究
王之千, 毛保全, 朱锐, 白向华, 韩小平
(陆军装甲兵学院 兵器与控制系, 北京 100072)
0 引言
广义上振荡流指流体在周期振荡边界条件下的流动特性。国内外众多学者根据不同的研究背景,对振荡流进行了相应研究[1-2]。Mentzoni等[3]基于Navier-Stokes方程提出了一种与海洋应用有关的振荡流动条件下多孔板水动力二维黏性流场模型,求得了解析解,并通过实验验证了模型的准确性。Fu等[4]采用实验方法测量了通过多孔通道的速度、测试段的压降和沿热表面的温度,研究了稳态和振荡气流作用下多孔通道的传热特性。Ni等[5]将实验和仿真相结合提出了一种定量描述含多孔介质振荡流动特性的方法,从而指导基于振荡流器件的设计。Pamuk[6]通过多组实验研究了振荡流动条件下流体的传热问题,得到了一种新的振荡流努塞尔数相关关系,为估计振荡流传热提供可靠方法。
黏弹性胶体材料属于非牛顿流体,外力作用下在阻尼缓冲器中作周期往复运动时黏弹性胶体的流动过程可看作振荡流。然而上述振荡流的研究背景、材料及边界条件与黏弹性胶体阻尼缓冲器均不相同,且主要以多孔、微孔流动或传热导热为主,加之黏弹性流体独特的非线性,应用于黏弹性胶体阻尼缓冲器中较为困难。
随着分数阶导数的提出,分数Maxwell模型被证明可以较好地模拟黏弹性流体的流动过程[7-9]。Yan等[10]等将分数Maxwell方法用于研究滚动运动中的管道振荡流动,以模拟船上管道受到海水振荡时的情况,得到了滚动运动中管内速度梯度及变化情况。Tan等[11-12]利用连续分数导数离散拉普拉斯逆变换,研究了黏弹性流体在平面突然运动及两平行板间的分数Maxwell流体模型,并求得了速度和应力的解析解。Zhang等[13]研究了黏弹性纳米流体在多孔介质中的二维非定常边界层流动和传热传质问题,提出了一种含布朗扩散和热迁移的时间- 空间分数Maxwell导热模型,分析了参数对速度、温度和浓度分布的影响。上述研究从数学角度很好地描述了黏弹性流体的流动特性,但值得注意地是,这些表达式模型参数往往通过数值方法得出,并不始终在物理和工程上保持合理性[14]。
准态特性的提出解决了上述问题,它将数学与物理意义相结合,使模型参数与实际研究对象联系更为紧密[15]。虽然准态特性已提出半个多世纪,但直到近几年才在分数Maxwell模型中得到广泛应用[16]。Holder等[17]通过研究胶原凝胶的黏弹性力学性能,证明了分数Maxwell模型可以很好地描述成熟胶原凝胶力学性能的时间依赖性。Jaishankar等[18-19]构建了含准态特性的剪切变形分数Maxwell模型,通过与实验数据对比,表明在一定时间尺度范围内,模型预测的长时间幂律响应与实验数据具有很好的一致性,并证明了准态特性可准确描述复杂流变界面,有助于确定材料对其他变形模式的响应。另外,文献[20-22]中对准态特性引入分数Maxwell模型等分数阶本构模型进行了详细研究。
黏弹性胶体材料在阻尼缓冲器中运动时具有较强的非线性和黏弹性,呈现非牛顿流体特性,而采用以准态特性为参数的分数Maxwell模型模拟黏弹性流体在圆管内和平板间的振荡流鲜有报道,同时应用其预测滞回曲线以指导阻尼缓冲器设计的报道也较少。因此,本文针对黏弹性胶体在阻尼缓冲器阻尼孔和节流间隙中振荡流问题,设定振荡边界条件,构建以准态特性为参数的分数Maxwell模型,并与牛顿流体模型进行对比,研究黏弹性流体在圆管内和两平板间的振荡流动特性。通过实验验证分数Maxwell模型模拟黏弹性胶体阻尼缓冲器振荡流的准确性。
1 分数Maxwell振荡流模型构建
1.1 分数Maxwell模型
广义黏弹性模型是将弹簧与黏壶串联看作一个机构元件,其本构关系可写为
(1)
采用Maxwell模型串联两个弹簧壶机构元件(κ,α)和(ψ,β)(见图1),其中ψ为准态特性(Pa·sβ),β为分数阶指数。由Maxwell模型关系可得
σa=σb=σ,
(2)
εa+εb=ε,
(3)
式中:σa和εa分别为弹簧壶元件(κ,α)的应力与应变;σb和εb分别为弹簧壶元件(ψ,β)的应力与应变;σ和ε分别为Maxwell模型的总应力与总应变。
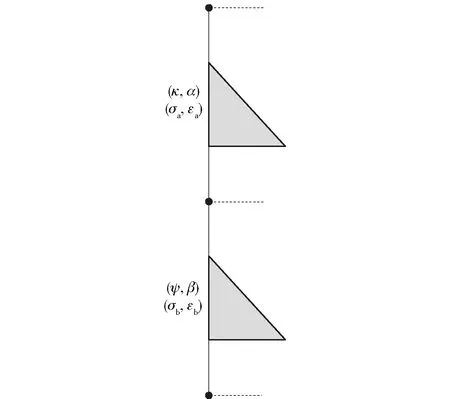
图1 分数Maxwell模型Fig.1 Fractional Maxwell model
(1)式代入(2)式、(3)式,得
(4)
即分数Maxwell模型为
(5)
1.2 结构及简化
某型黏弹性胶体阻尼缓冲器结构如图2所示。阻尼缓冲器支座用于连接阻尼缓冲器和安装机构,起一定承力作用。将黏弹性胶体材料通过黏弹性胶体注入器注入阻尼缓冲器腔室中。根据需要调整黏弹性胶体材料的填充量,使阻尼缓冲器具有一定的预压力,称为初始预紧力。当阻尼缓冲器受到外界压力或冲击大于初始预紧力时,活塞杆推动活塞压缩阻尼缓冲器腔室内的黏弹性胶体材料。胶体材料被迫流过节流间隙和活塞上的阻尼孔,产生黏滞力,阻碍活塞前行,这一过程中外力转化为热能和势能,消耗和存储。当外力被撤销时,冲击力小于初始预紧力,黏弹性胶体材料自行膨胀,释放压缩过程中储存的势能,将活塞推回到初始位置,而通过阻尼孔和节流间隙被挤入前腔体的胶体材料流回后腔体,等待下次冲击或压力。

图2 某型黏弹性胶体阻尼缓冲器示意图Fig.2 Schematic diagram of a viscoelastic elastomer shock absorber
根据黏弹性胶体阻尼缓冲器振荡流实际工况,黏弹性胶体在阻尼缓冲器阻尼孔中的运动可简化为流体中心以ucos(ωt)(u为一个恒定的振幅,表示速度;ω为振荡频率)的流速在圆管内振荡流动,而靠近管壁的流体流速为0 m/s(见图3(a)所示,即流体在两平行板间以ucos(ωt)的速度左右振荡流动,而两平板始终保持不动);黏弹性胶体在节流间隙中振荡流的运动可简化为一板不动、一板以ucos(ωt)的速度振荡运动(见图3(b)所示,即上板以ucos(ωt)的速度左右振荡流动,下板始终保持不动,流体由于粘性在上板的带动下左右振荡流动)。图3中:L为阻尼孔或节流间隙间距;p为一个恒定的振幅,表示压力。
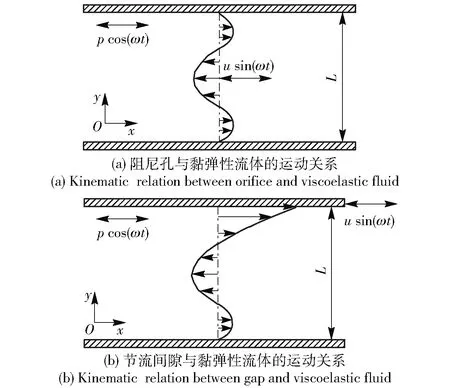
图3 阻尼缓冲器结构与黏弹性胶体的运动关系简化Fig.3 Simplified kinematic relation between shock absorber structure and viscoelastic elastomer
1.3 控制方程
流体运动中总动量的时间变化率等于其自身体积力和相互作用表面力的总和。将加速度a看作单位质量流体动量随时间的变化率,根据动量平衡率的牛顿运动定律可知:
ma=∑F,
(6)
式中:m为质量;F为体积力和表面力总和。
与坐标系无关的运动方程矢量表达式为
(7)
式中:f为单位体积力;ρ为黏弹性流体密度;σ为应力张量。
考虑阻尼缓冲器中黏弹性流体介质运动时黏性较大、总质量较小,体积力远小于黏性力,因此将体积力忽略不计。则有
(8)
即振荡流运动方程可写为
(9)
其中考虑沿x轴方向外加振荡的压力梯度[23-24],如图3所示,其形式为
(10)
式中:u(t,y)和σ(t,y)分别表示在时刻t空间位置y处的流速和应力。
(11)
(12)
由Riemann-Liouville分数阶微积分公式可知:
(13)
式中:t>0,θ>0,ϑ=「θ⎤表示不小于θ的最小整数,且
(14)
式中:Γ(z)是伽马函数。
假定边界无滑移,由图3可得相应的初始和边界条件:
1)阻尼孔为
(15)
2)节流间隙为
(16)
1.4 无量纲分析
采用Π定理引入如下无量纲变量:
(17)
式中:η为准态特性无量纲系数。
(17)式的无量纲变量分别代入(11)式、(12)式中,得到分数Maxwell振荡流无量纲方程(以下变量均为无量纲变量,为简便起见,省略无量纲标记“*”):
(18)
(19)
对应的阻尼孔和节流间隙的无量纲初始和边界条件为
(20)
(21)
1.5 数值求解

(22)
(23)
o()为高阶无穷小,则
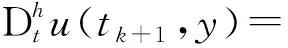
(24)
式中:r为高阶项系数;t0=0;h0=1;hi=(i+1)1-h-i1-h,i=0,1,…,k.
则
(25)
式中:高阶项系数r=2-h;hj=(j+1)1-h-j1-h,j=0,1,…,k. 则

(26)
同理,利用中心差分定理:

(27)
根据分数阶积分定义:
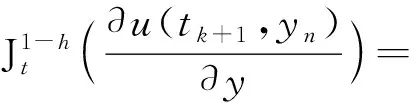
(28)
(29)

(30)
(31)
另外,牛顿流体模型根据(1)式可写为
(32)
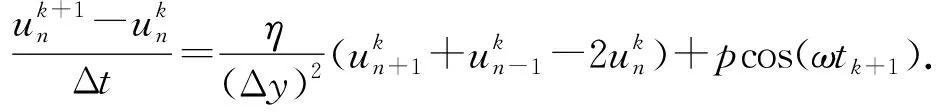
(33)
2 数值结果及讨论
将模型和边界条件代入数学仿真软件MATLAB中,为保证结果收敛,选取时间步长Δt=0.001、空间步长Δy=0.025. 通过数值计算,对比分数Maxwell模型和牛顿流体模型的流动特性,选取基本模型参数为α=0.8,β=0.3,η=0.2.
2.1 节流间隙数值模拟
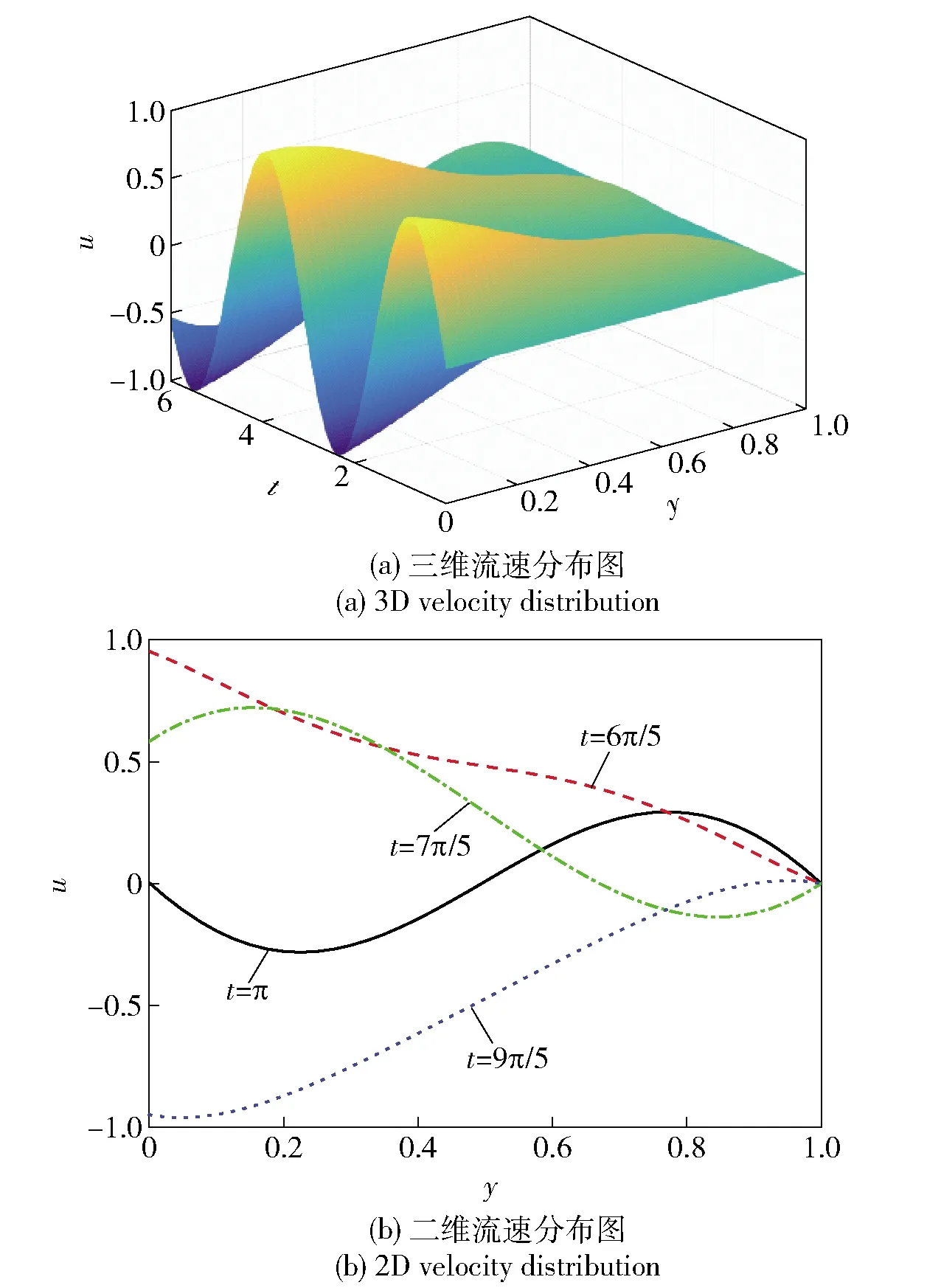
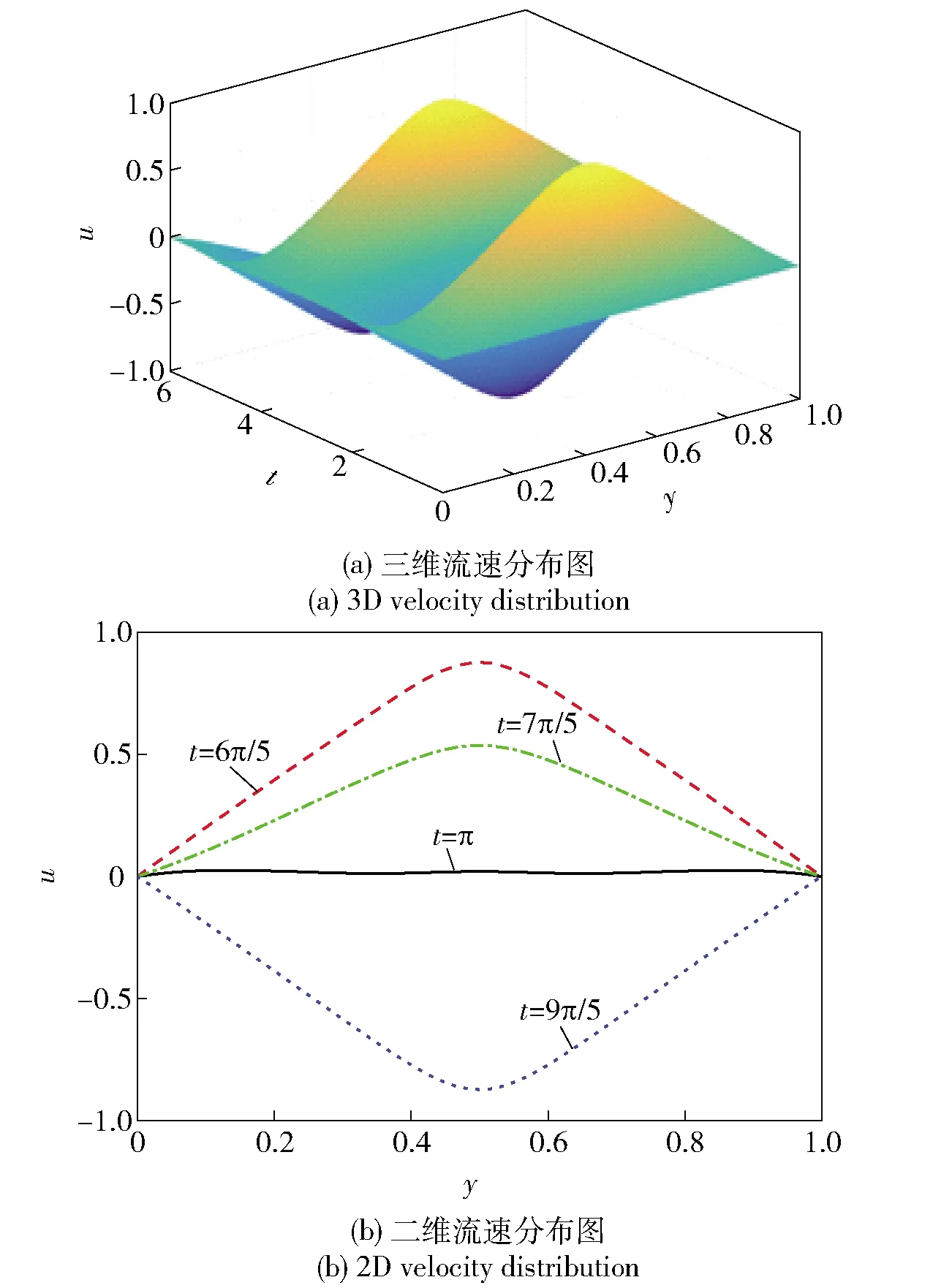
图4 ω=2时分数Maxwell模型节流间隙流速分布(α=0.8,β=0.3,η=0.2)Fig.4 Flow velocity distributions of the fractional Maxwell model in the gap for ω=2 (α=0.8,β=0.3,η=0.2)
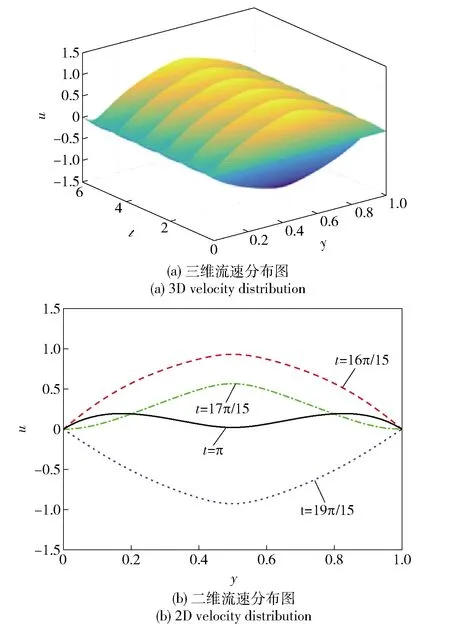
分数Maxwell模型和牛顿流体模型在振荡频率ω为2时节流间隙振荡流流速分布数值结果分别如图4和图5所示,其中,u为无量纲速度,t为无量纲时间,y为无量纲位移。结合图4和图5可知,两种模型均发生周期振荡,且靠近运动板的流体(y=0处)流速变化幅度最大,而靠近停止板的流体(y=1处)流速始终保持为0. 对比图4(a)和图5(a)两种模型节流间隙振荡流流速分布三维图可以看出,两种模型在平板间随时间变化的流速分布趋势类似,均呈平缓的梯度分布,其振荡幅度逐渐降低,但分数Maxwell模型流速分布较牛顿流体模型流速分布非线性更强。图4(b)和图5(b)分别为两种模型在一个周期内随时间增加时的流速分布二维图。从图4和图5中可以看出在一个周期内随着时间的增长,两种模型在y=0处的流体流速振荡幅度最大,并通过振荡将流速传递至相邻位置,对比可以看出分数Maxwell模型流速分布较牛顿流体模型非线性明显,而牛顿流体模型在流速最大时发展近似呈直线。
图6和图7分别为ω=6时分数Maxwell模型和牛顿流体模型节流间隙振荡流流速分布。对比图6(a)和图7(a)可以看出:分数Maxwell模型的流速分布随y的增加由较大的流速降至较低流速后降为0,变化幅度较大;而牛顿流体模型流速下降较为平缓,有明显过度。图6(b)和图7(b)为一个周期内两种模型随时间增加的二维流速分布,可以看出分数Maxwell模型较牛顿流体模型具有较强非线性,振荡传递性较为明显。结合图4~图7可以看出:振荡频率ω对分数Maxwell模型影响较大,而对牛顿流体模型影响较小,原因在于分数Maxwell模型具有较强的非线性,后运动的流体流速受前一刻流体流速和频率影响均较为明显;而牛顿流体模型中后运动的流体流速仅受前一刻流体流速的影响,频率对其影响较小,这也是图7(a)中牛顿流体模型相比Maxwell模型流速分布下降平缓的原因。因此,分数Maxwell模型模拟的流体较牛顿流体模型具有较强的非线性。

图7 ω=6时牛顿流体模型节流间隙流速分布(η=0.2)Fig.7 Flow velocity distributions of the Newtonian fluid model in the gap for ω=6 (η=0.2)
2.2 阻尼孔数值模拟
图8和图9分别为ω=2时分数Maxwell模型和牛顿流体模型阻尼孔振荡流流速分布数值结果,从中可以看出两种模型均发生周期振荡,且在阻尼孔内的流速分布曲线沿y=0.5的轴线对称。对比图8和图9中ω=2时阻尼孔振荡流流速分布可知,两种模型的流速分布趋势类似,一个周期内同一时刻分数Maxwell模型较牛顿流体模型的非线性稍强,当振幅较大时牛顿流体模型流速分布在0 图8 ω=2时分数Maxwell模型阻尼孔流速分布(α=0.8,β=0.3,η=0.2)Fig.8 Flow velocity distributions of the fractional Maxwell model in the orifice for ω=2 (α=0.8,β=0.3,η=0.2) 图9 ω=2时牛顿流体模型阻尼孔流速分布(η=0.2)Fig.9 Flow velocity distributions of the Newtonian fluid model in theorifice for ω=2 (η=0.2) 图10和图11分别为ω=6时两种模型的阻尼孔流速分布。对比图10(a)和图11(a)流速分布三维图,可以看出分数Maxwell模型流速分布形状呈柱塞形,而牛顿流体模型流速分布呈抛物线状。对比图10(b)和图11(b)两种模型二维流速分布图可知,牛顿流体模型流速分布振荡传递性明显较分数Maxwell模型弱,因此其非线性也较弱。结合图8~图11可以判断分数Maxwell模型对频率的依赖性更强,振荡频率不同流速分布也不同,而牛顿流体模型则对频率依赖性较弱,该结果与节流间隙类似。 图10 ω=6时分数Maxwell模型阻尼孔流速分布(α=0.8,β=0.3,η=0.2)Fig.10 Flow velocity distributions of the fractional Maxwell model in the orifice for ω=6 (α=0.8,β=0.3,η=0.2) 图11 ω=6时牛顿流体模型阻尼孔流速分布(η=0.2)Fig.11 Flow velocity distributions of the Newtonian fluid model in the damping orifice for ω=6 (η=0.2) 图12 ω=6时各参数变化对分数Maxwell模型阻尼孔y=0.5处应力- 应变率分布影响Fig.12 Influences of parameters on the stress-strain rate distributions of the fractional Maxwell model in y=0.5 of the damping orifice for ω=6 图13 ω=6时不同η对牛顿流体模型阻尼孔y=0.5处应力- 应变率分布影响Fig.13 Influence of η on the stress-strain rate curves of the Newtonian fluid model in y=0.5 of damping orifice for ω=6 为检验分数Maxwell模型对黏弹性胶体阻尼缓冲器滞回曲线的预测性,采用MTS 810型电液伺服疲劳实验机(如图14所示)加载正弦波激励模拟阻尼缓冲器的实际工况。为简化模型运算,仅考虑阻尼孔的影响,黏弹性胶体阻尼缓冲器实验样机采用单出杆阻尼孔式,其结构如图2去除节流间隙所示,具体尺寸参数如表1所示。 图14 MTS 810型电液伺服疲劳实验机Fig.14 MTS 810 electro-hydraulic servo fatigue testing machine 表1 黏弹性胶体阻尼缓冲器结构尺寸 Tab.1 Basic parameters of viscoelastic elastomer shock absorber 阻尼孔直径/mm活塞直径/mm最大行程/mm2.52012 为使黏弹性胶体阻尼缓冲器实际工况与模型初始及边界条件相近,采用文献[26]的实验结果,当位移小于等于1 mm时,边界滑移现象不明显。因此,选择加载频率振幅为0.3 mm,由于阻尼缓冲器无法承受拉应力,实验过程中采用疲劳实验机先将阻尼缓冲器压缩0.3 mm,后分别加载8 Hz、10 Hz的正弦波激励频率及0.3 mm的振荡振幅,并采集阻尼缓冲器滞回曲线。表2胶体材料及模型参数代入分数Maxwell模型中,得到应力- 应变率曲线,对应变率进行积分可得模型的应力- 应变曲线,将其看作模型所模拟的阻尼缓冲器滞回曲线。 表2 胶体材料及模型参数[27] 图15 频率为8 Hz时实验滞回曲线和数值模拟滞回曲线对比Fig.15 Test and simulated hysteretic curves at 8 Hz 图15和图16分别为8 Hz和10 Hz时疲劳实验机实验所得滞回曲线和分数Maxwell模型模拟所得滞回曲线,实验和模拟结果如表3所示。对比图15和图16不同频率下分数Maxwell模型模拟的黏弹性胶体缓冲器滞回曲线与实验所得滞回曲线可知:数值模拟的滞回曲线与实验所得滞回曲线具有相同的形状趋势,均呈椭圆形,其能量吸收率、最大位移、最小力和最大力与实验结果相近,相对于实验结果平均误差分别为3.60%、2.55%、1.81%和3.77%. 数值模拟阻尼缓冲器滞回曲线时,能量吸收率和曲线形状趋势是考察模型准确与否的主要指标。分数Maxwell模型模拟阻尼缓冲器滞回曲线形状趋势与实验结果相近,且能量吸收率平均误差为3.60%. 因此,分数Maxwell模型可用以预测黏弹性胶体阻尼缓冲器滞回曲线的形状及变化趋势,从而指导黏弹性胶体阻尼缓冲器的设计。加之其非线性较强,可很好地描述黏弹性胶体的黏弹性特性。 图16 频率为10 Hz时实验滞回曲线和数值模拟滞回曲线对比Fig.16 Test and simulated hysteretic curves at 10 Hz 表3 实验与数值滞回曲线结果及误差对比 Tab.3 Test and simulated results errors of hysteretic curves 不同激励频率滞回曲线结果最大力/kN最小力/kN最大位移/mm能量吸收率/%8Hz时实验结果2.49750.19390.5879.298Hz时数值模拟结果2.45390.18870.5775.9110Hz时实验结果2.48570.23600.5479.3610Hz时数值模拟结果2.36160.23820.5277.03数值模拟相对实验结果误差最大力误差/%最小力误差/%最大位移误差/%能量吸收率误差/%8Hz时1.752.681.724.2610Hz时4.990.933.372.94平均误差3.371.812.553.60 本文根据黏弹性胶体阻尼缓冲器受力时周期往复运动的实际工况,简化黏弹性胶体在阻尼缓冲器阻尼孔和节流间隙中的振荡流动过程,设定振荡流初始和边界条件,提出并构建了含准态特性参数用于研究黏弹性胶体阻尼缓冲器振荡流的分数Maxwell模型,采用有限差分法求得数值解。通过与牛顿流体模型结果进行对比,分析了不同振荡频率下的流速分布及各参数对应力- 应变率曲线的影响。采用疲劳实验机加载频率模拟阻尼缓冲器实际工况,采集滞回曲线并与分数Maxwell模型模拟结果进行对比,验证了模型的可预测性。数值及实验结果表明: 1)分数Maxwell模型流速分布较牛顿流体模型非线性强,且具有较强的频率依赖性;不同参数下,分数Maxwell模型应力- 应变率曲线均呈椭圆形,而牛顿流体模型应力- 应变率曲线呈直线。 2)随着参数α、β和η的增加,分数Maxwell模型的应力- 应变率曲线椭圆长轴沿逆时针旋转。 3)分数Maxwell模型模拟的滞回曲线与实验所得滞回曲线具有相同的形状趋势,均呈椭圆形,且相对于实验结果能量吸收率平均误差为3.60%. 因此,分数Maxwell模型可模拟黏弹性胶体在阻尼缓冲器阻尼孔和节流间隙中振荡流的流动特性,用以预测黏弹性胶体阻尼缓冲器滞回曲线的形状及变化趋势,从而指导黏弹性胶体阻尼缓冲器的设计。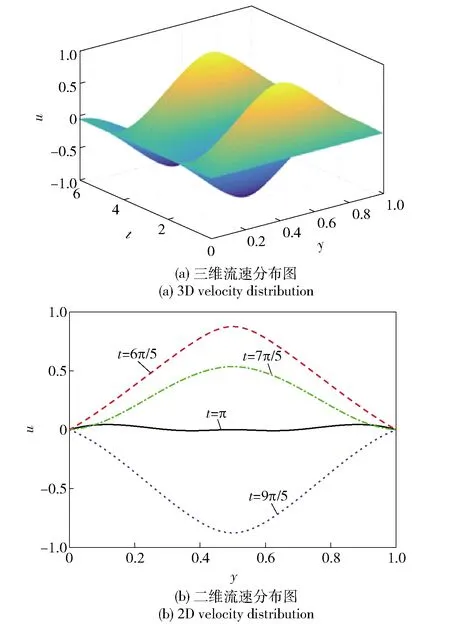

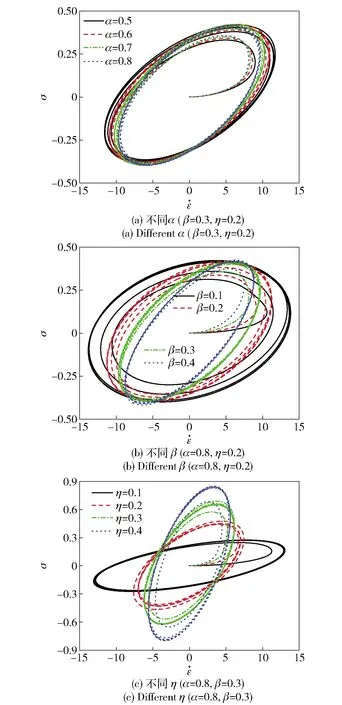
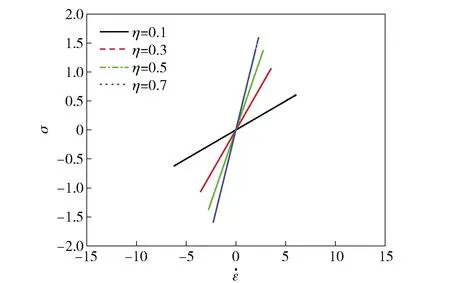
2.3 参数变化影响分析
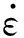
4 实验验证





4 结论

