弹丸在炮口的状态参数对地面密集度影响研究
钱林方, 陈光宋, 王明明
(1.西北机电工程研究所, 陕西 咸阳 712099; 2.南京理工大学 机械工程学院, 江苏 南京 210094)
0 引言
火炮发射无动力飞行弹丸的地面密集度是衡量中大口径火炮性能优劣的一个重要指标,影响密集度的主要因素有弹丸在炮口的状态参数、弹丸参数(物理和几何)、气象条件、气动载荷等随机误差。弹丸在炮口的状态参数由火炮发射过程赋予,理清弹丸在炮口的状态参数误差对地面密集度影响,为火炮总体设计提供依据,对提高火炮射击精度具有重要意义。
火炮射击精度问题一直是火炮设计和工程应用研究的热点和难点。众多的国内外学者在射击精度方面发表了大量研究成果。例如:韩子鹏等[1]通过建立不同复杂程度的外弹道方程,系统地分析了影响弹丸落点分布的因素,并给出了炮口状态参数对射击精度影响的物理解释;郭锡福[2]对远程火炮射击精度的计算分析模型、影响因素、试验技术等进行了深入研究;王宝元[3]讨论了影响火炮射击密集度的因素,并归纳了火炮武器型号研制和提高射击密集度所采取的技术措施;芮筱亭等[4]基于最大熵法对武器系统的射击密集度进行了分析,结果显示,弹丸落点的分布为具有偏态性质的类正态分布;张领科等[5]计算分析了点火具点火延迟时间、底排装置工作时间和底排药剂部分脱落质量偏差对射程散布影响;曹宁等[6]利用逐步回归法研究了弹丸初速、质量和偏心距等因素对火炮射击密集度影响;张海燕等[7]基于拉丁超立方试验设计方法和极差分析法进行了射击密集度灵敏度计算,分析了结构参数对射击密集度的影响规律;王瑞林等[8]研究了高、低射击频率对射击精度的影响;王丽群等[9]提出一种面向指标要求的随机因素参数区间计算方法,在给定密集度指标的前提下,给出了最终的优选参数方案;李建中等[10]分析了影响弹丸起始扰动的重要参数,重点研究了弹丸质量偏心对大口径火炮射击精度影响;Qian等[11]采用基于统计信息的区间方法分析了弹炮耦合系统的不确定性传播问题。在国际上,国际弹道会议以及相关的其他会议和学术论文等对火炮射击精度相关的理论和技术进行了探讨,例如:Dursun[12]探讨了炮架刚度、弹丸初速和制造公差等对弹丸散布影响;Rabbath等[13]通过比较样本标准差置信区间的假设检验方法来评估火炮的射击精度;Khalil等[14]利用基于工程算法的火箭弹、导弹、炮弹快速设计平台PRODAS软件建立了M107型155 mm弹丸6自由度的发射动力学模型,分析了弹丸质量、初速、炮口摆角与偏角对射击精度影响。国内外众多的研究和取得的成果对认识和深入研究火炮射击精度提供了重要的帮助,也为进一步提高火炮射击精度奠定了良好的基础。
近年来,不确定性问题逐渐成为国内外学者研究的热点,开展了深入广泛的研究,发展了多种不确定性量化和分析方法,例如概率方法[15-16]、非概率方法[17-18]、混合方法[19-21]等,这些方法为解决工程中的具体问题提供了有效途径。最近,稀疏网格数值积分(SGNI)方法被成功引入到不确定性传播分析中,并取得了较好的效果[22-23],它是基于一种特殊的张量积法则,通过低阶积分点的嵌入式配置方法,在多变量空间构建高阶的积分点,形成积分精度较高的SGNI点,有效避免传统高维积分法因维度较大而引起的“维度灾难”问题。
本文基于6自由度刚体外弹道方程,考虑无动力飞行弹丸参数和炮口状态参数误差影响,采用SGNI获得弹丸落点的统计特性参数,在此基础上利用最大熵估计方法,获得弹丸落点散布的统计特性。最后,通过与蒙特卡洛方法对比验证了本文方法的有效性,并利用本文方法计算分析了某155 mm加榴炮的地面密集度。
1 刚体外弹道方程
将弹丸视为空间运动的刚体,则弹丸有6个自由度。定义惯性坐标系为Oixiyizi,弹体坐标系为Opxpypzp,其中Op为弹丸的几何中心点,Opxp沿弹轴方向,Opypzp平面垂直于Opxp,则弹丸的运动可用Opxpypzp相对Oixiyizi的3个平动位移量u和3个角度位移量ψ描述,相应速度量分别为v和ω,加速度分别为a和ε.
为推导动力学方程方便,令
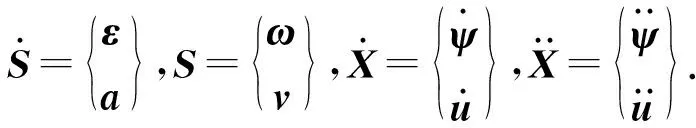
(1)
弹丸运动关系可表示为
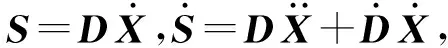
(2)
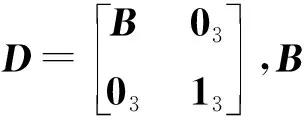
弹丸运动的虚功率方程可表示为
(3)
由外弹道理论可知,作用在弹丸上的合外力f包含了阻力fx、升力fy、马格努斯力fz、哥氏力fk和重力fg,则合力f为
f=fx+fy+fz+fk+fg.
(4)
作用在弹丸上的合外力矩t包含了静力矩tz、赤道阻尼力矩tzz、极阻尼力矩txz、马格努斯力矩ty,则合外力矩t为
t=tz+tzz+txz+ty.
(5)
(2)式代入(3)式,根据变分原理可得弹丸动力学方程为
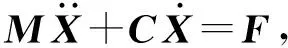
(6)
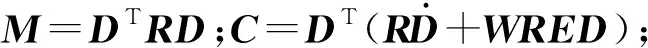
F=DTQ.
(7)
(6)式中左端两项均为惯性力,其中:第1项为主惯性力,与加速度有关;第2项为附加惯性力,包括离心力、哥氏力等。
2 弹丸落点统计参数的求解
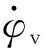
2.1 基于SGNI的弹丸落点统计矩求解
考虑上述参数影响,无动力飞行的弹丸外弹道方程可表示为
(8)
式中:t为弹丸飞行时间。
随机初始条件为弹丸在炮口的状态参数
(9)

为分析参数误差对弹丸落点分布的影响,需要根据已知随机参数ξ的联合概率密度函数fξ(ξ)求解方程(8)式获得弹丸落点的概率分布。记弹丸落点的纵向和横向位置分别为x=g(ξ)和z=h(ξ),弹丸落点中心矩即是对地面密集度的衡量。以纵向落点分布为例,落点分布的e阶原点矩μe与中心矩ce分别为
(10)
(11)
式中:Ωξ为随机参数ξ的空间。由前4阶统计矩转化而来的均值μ、标准差σ、偏度τ和峰度κ分别为
(12)
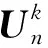
(13)
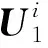
对于上述积分点,相应的积分权重可根据Smolyak方法[25]计算:
(14)
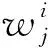
(15)
ωi(ξ)=(ξ-ξ1)(ξ-ξ2)…(ξ-ξi).
(16)

2.2 基于最大熵原理的弹丸落点分布估计
最大熵原理[26]可以描述为在给定部分信息推断概率分布时,所有可能的分布中存在一个使信息熵取最大值的分布,该分布是最小偏见的。文献[27]对常见分布的最大熵估计进行了推导和证明,并给出了一般分布的最大熵估计求解方法。考虑到弹丸落点服从类正态分布[4]的特性,可利用该方法对弹丸落点分布进行估计。
以纵向落点x=g(ξ)分布为例,定义弹丸落点参数x的信息熵S为
(17)
式中:fx(x)为弹丸纵向落点的概率密度函数;Ωx为积分空间。
将落点分布的前r阶中心矩(本文中取r=4)作为信息熵约束条件,则可建立如下求解fx(x)的优化模型:
(18)
(18)式为等式约束优化问题,可采用拉格朗日方法进行变换,定义如下形式的拉格朗日函数:
(19)
式中:λe(e=0,1,…,r)为拉格朗日乘子。令(19)式对fx(x)求导等于0,则满足最大熵原理的fx(x)[27]可表示为
(20)
将表达式(20)式代入约束方程可得如下非线性方程:
(21)
(21)式中待定系数λe与方程数相同,理论上存在一组最优解,通常将(21)式的非线性方程转化为无约束优化问题来求解,定义误差函数最小,即
(22)
式中:λ={λ0,λ1,…,λr}T.
为确保上述优化问题能够得到较为准确的解,本文利用遗传算法和序列二次规划的方法进行求解,以此来满足全局搜索和局部精细求解的目的。先通过遗传算法求解(22)式,并将计算得到的结果作为初始值,利用序列二次规划方法计算获得最终的解。计算落点统计矩和概率分布的流程如图1所示。
3 算例分析
以某155 mm加榴炮为研究对象,分析最大射程的弹丸落点散布,最大射程角为51°.
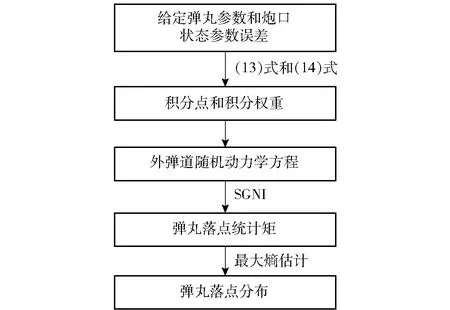
图1 计算流程Fig.1 Flowchart of computation
3.1 有效性验证

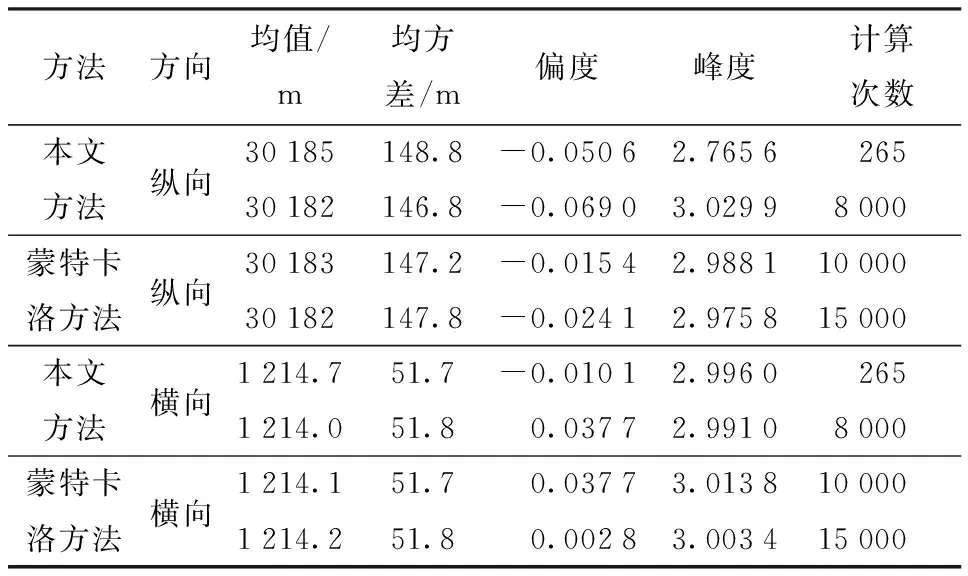
由于难以获得弹丸落点分布统计特性的解析解,为了验证本文方法的有效性,本文将蒙特卡洛方法的计算结果作为参考解。采用稀疏网格积分的精度水平取k=2,根据前文的推导,n=11个参数的总积分点数N=2n2+2n+1=265. 计算得到的弹丸落点纵向和横向概率密度函数(PDF)如图2和图3所示,落点参数的统计值如表2所示。从计算结果可看出,本文方法和蒙特卡洛方法获得的落点统计分布特性吻合得很好,从而验证了本文方法的有效性。

表1 弹丸不确定性参数
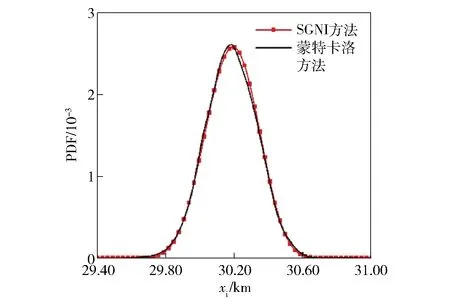
图2 落点纵向分布Fig.2 Longitudinal dispersion of projectiles
3.2 弹丸在炮口的单状态参数影响分析
本节考虑7个炮口状态参数单独作用对弹丸落点密集度影响。参考文献[3]和型号研制工程经验,将参数范围进行适当放大,给定炮口状态参数的均值和均方差的范围如表3所示;弹丸参数的统计特性与表1所示相同,在具体分析中也可根据不同型号火炮的特点确定对应的参数范围。采用稀疏网格积分的精度水平取k=2,根据前文的推导,单变量的积分点数N=2n+1=7. 炮口状态参数误差与地面密集度的影响呈近似二次关系,为此,建立如下所示的炮口单状态参数均方差和落点均方差二次形式的参数化模型:
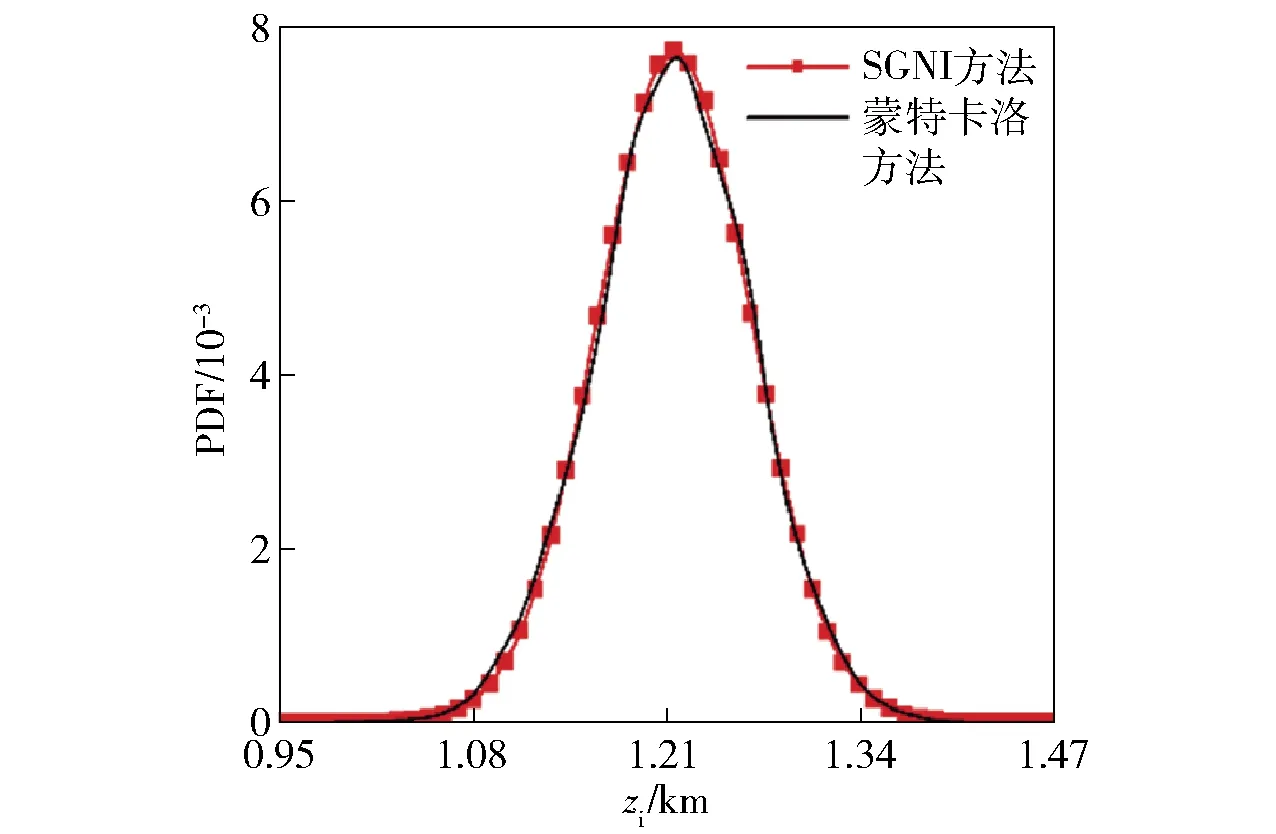
图3 落点横向分布Fig.3 Transverse dispersion of projectiles
表2 落点统计特性
Tab.2 Statistical parameters of projectiles dispersion
方法方向均值/m均方差/m偏度峰度计算次数本文纵向30185148.8-0.05062.7656265方法30182146.8-0.06903.02998000蒙特卡纵向30183147.2-0.01542.988110000洛方法30182147.8-0.02412.975815000本文横向1214.751.7-0.01012.9960265方法1214.051.80.03772.99108000蒙特卡横向1214.151.70.03773.013810000洛方法1214.251.80.00283.003415000

表3 弹丸在炮口的状态参数
(23)
(24)

(25)
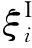
根据炮口单状态参数影响的数据,通过拟合得到各个模型系数如表4和表5所示,其中R2为拟合模型的可决系数。将(23)式、(24)式分别绘制成曲线得各炮口状态参数均方差对弹丸落点纵向和横向地面密集度Axi和Azi的影响规律,如图4~图10所示。
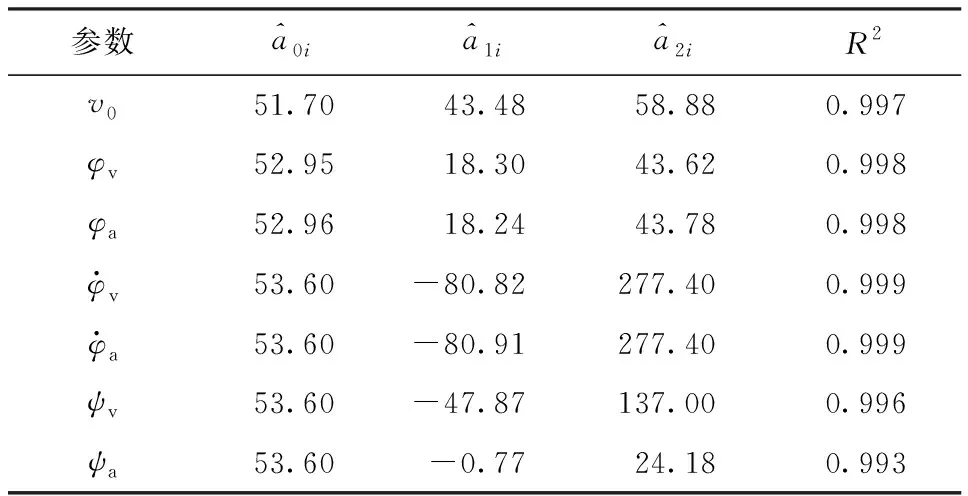
表4 模型(23)式的系数
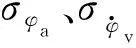
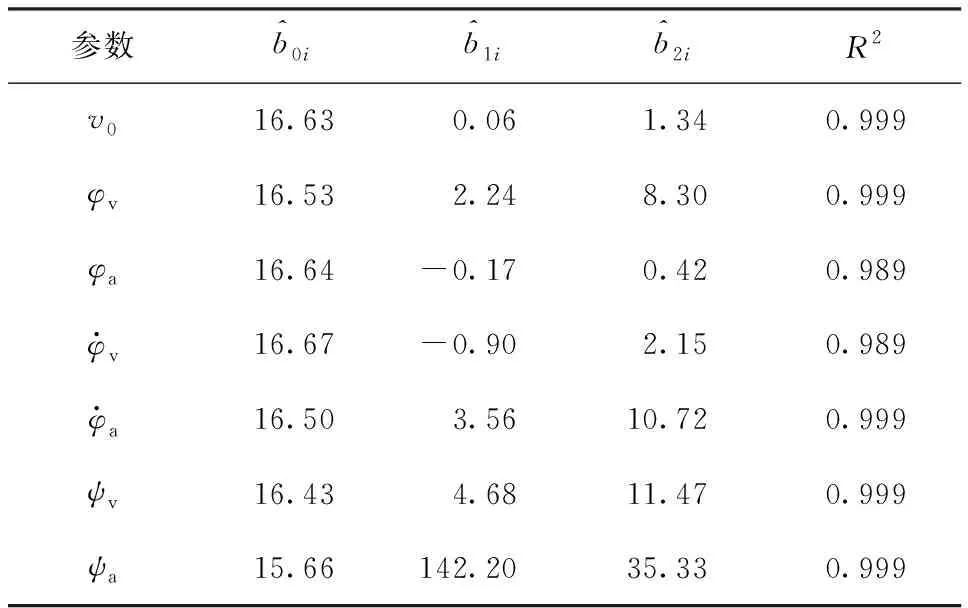
表5 模型(24)式的系数
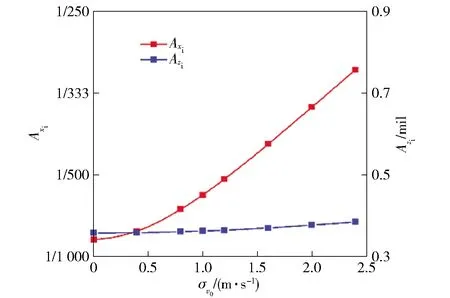
图4 初速均方差对地面密集度影响Fig.4 Effect of σv0 on ground dispersion
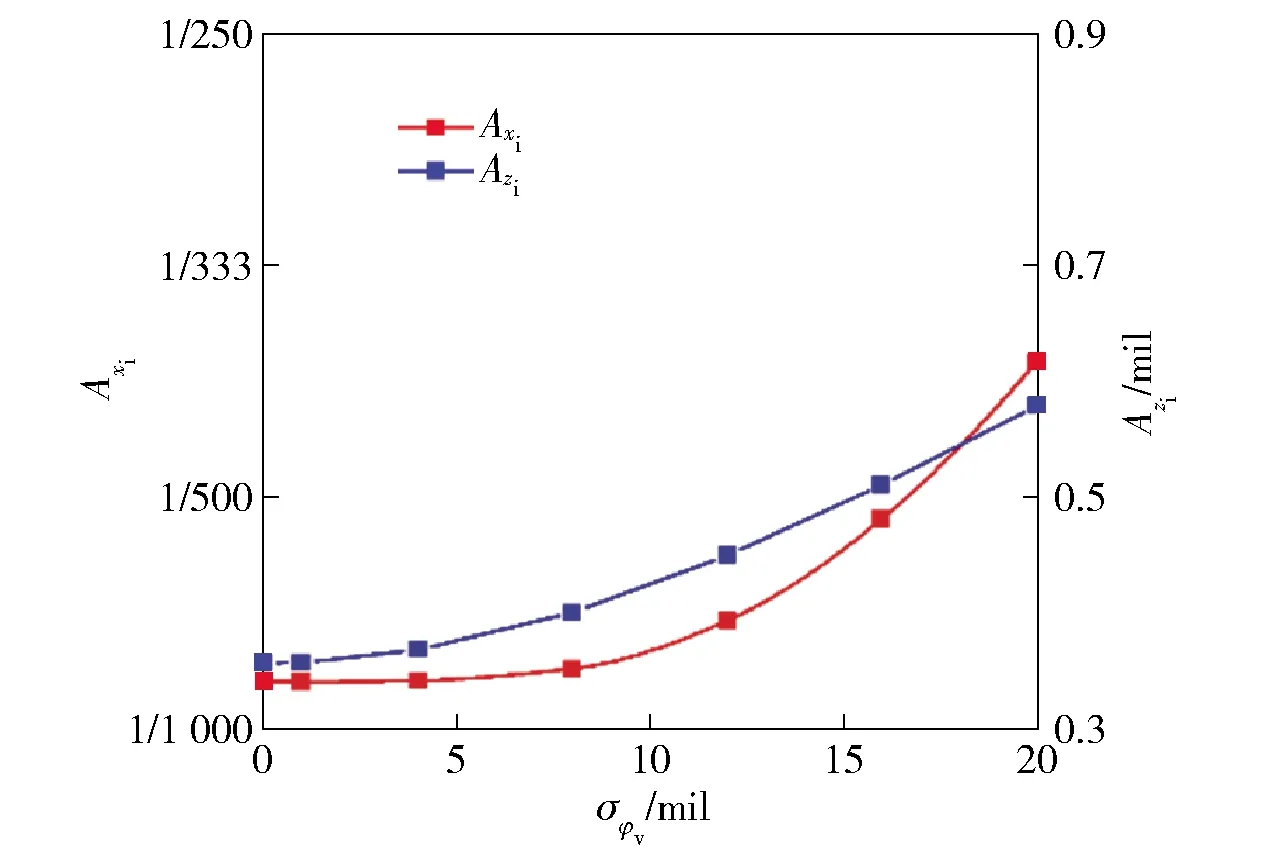
图5 高低摆角均方差对地面密集度影响Fig.5 Effect of σφv on ground dispersion

图6 方向摆角均方差对地面密集度影响Fig.6 Effect of σφa on ground dispersion
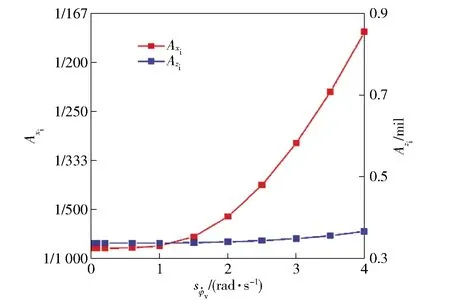
图7 高低摆角速度均方差对地面密集度影响Fig.7 Effect of on ground dispersion

图8 方向摆角速度均方差对地面密集度影响Fig.8 Effect of on ground dispersion
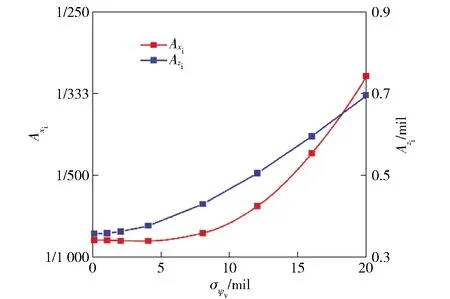
图9 高低偏角均方差对地面密集度影响Fig.9 Effect of σψv on ground dispersion
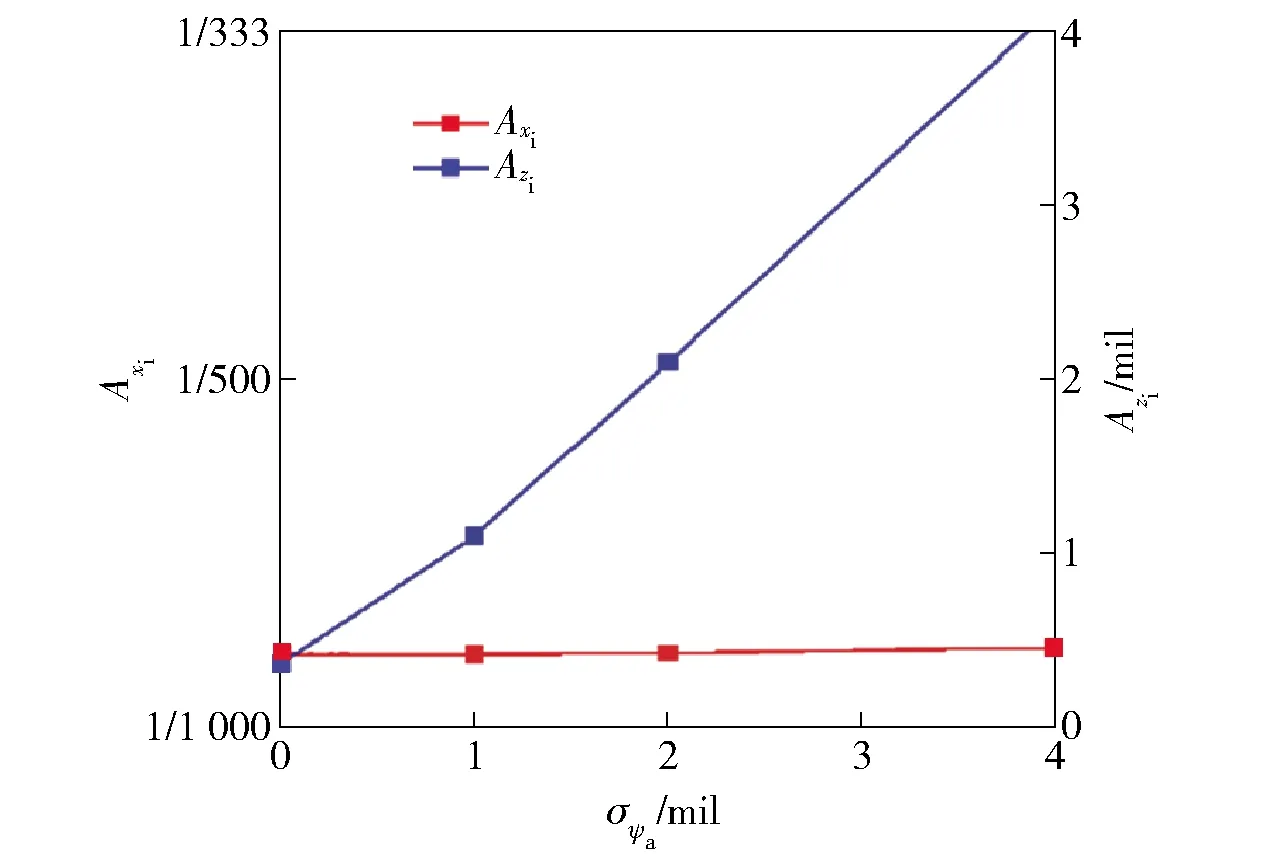
图10 方向偏角均方差对地面密集度影响Fig.10 Effect of σψa on ground dispersion
3.3 弹丸在炮口的多参数变量影响分析
弹丸在炮口的多状态参数影响的综合模型可表示为
(26)
(27)
式中:σxi0和σzi0为0阶综合模型,表达式为
(28)
其含义是仅考虑与表1中给定的弹丸参数统计特性时弹丸落点的均方差。
为验证该模型的准确性,在表3给定的炮口均方差范围内随机抽样5组,将(26)式、(27)式计算得到的结果和稀疏网格法得到的结果进行对比验证,结果如表6所示。从表6中可看出,(26)式和(27)式的计算结果和稀疏网格的计算结果吻合较好,从而验证了(26)式和(27)式的准确性和可行性。
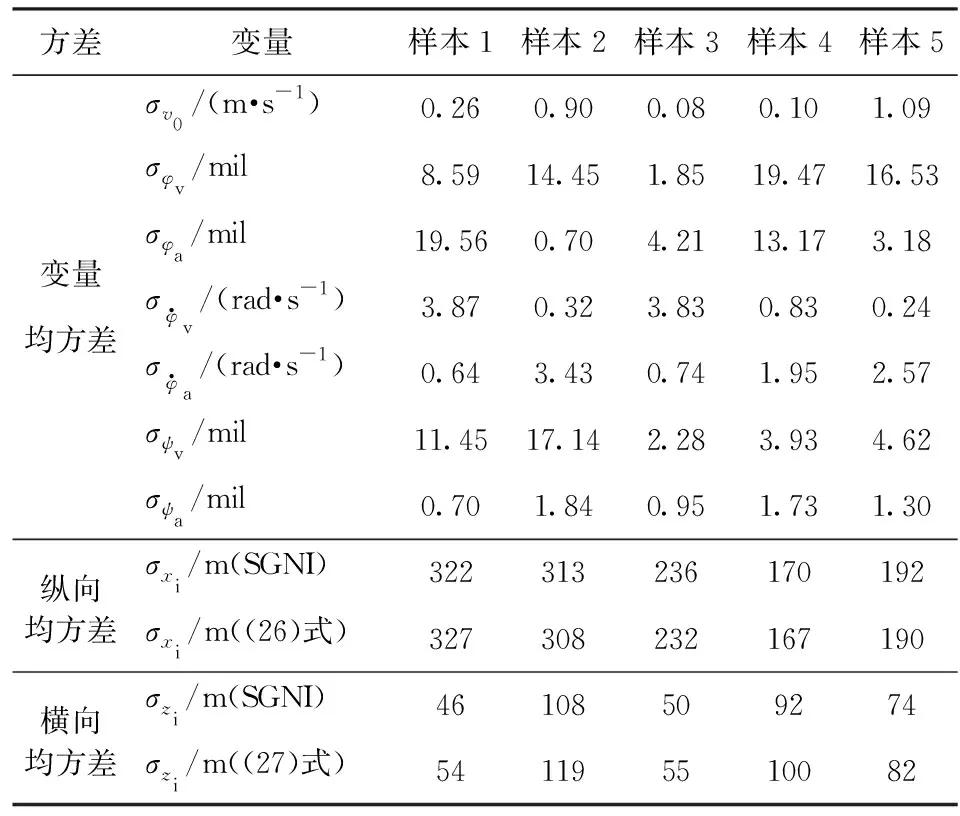
表6 弹丸在炮口的状态参数均方差样本
(26)式、(27)式对火炮射击精度设计具有指导作用,当给定弹丸最大射程密集度指标xi和zi时,(26)式和(27)式转换成由7个变量构成的空间超曲面方程fxi()=xi和fzi()=zi,火炮总体密集度设计的任务是根据给定的最大射程密集度要求xi和zi,设计一组火炮关键参数,确保弹丸在炮口的状态参数误差i的综合作用满足条件fxi(i)≤xi和fzi(i)≤zi.
以最大射程xi,max=30 km,纵向地面密集度Axi=1/300为例,由密集度计算公式反求弹丸纵向落点的均方差
(29)
另外,将表4中的模型系数带入(28)式得到仅考虑表1中给定的弹丸参数分布特性时弹丸纵向落点的均方差
(30)
式中:σxi0占(29)式均方差σxi的36%,此时,弹丸在炮口的状态参数分布导致的弹丸纵向落点均方差占64%.
4 结论
本文考虑了弹丸在炮口的状态参数误差影响,采用SGNI方法获得了落点散布的统计特性参数,并利用最大熵估计方法获得了落点散布的概率密度函数;重点分析了弹丸在炮口的状态参数误差对地面密集度影响规律,其结果可为火炮总体设计提供理论指导。根据理论分析和数值仿真结果,得到如下主要结论:
1) 通过与蒙特卡洛方法计算的统计矩和概率密度对比,验证了本文方法求解弹丸落点统计矩及其概率密度的正确性和有效性。
2) 通过炮口单状态参数对地面密集度影响分析,除了初速误差外,炮口其他6个参数的误差对地面密集度均有影响,而且其影响近似呈二次规律。
3) 通过炮口多状态参数对地面密集度影响分析,建立了弹丸在炮口的状态参数均方差与弹丸落点均方差之间的综合映射模型,该模型可为火炮射击密集度的总体设计提供理论指导。
4) 若以射程30 km,纵向地面密集度1/300为指标要求,则弹丸参数ξp对纵向地面密集度的贡献约为36%,弹丸在炮口的状态参数ξ0对纵向地面密集度的贡献约为64%.

