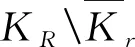三阶周期边值问题的正解
康文苗
(兰州理工大学理学院,甘肃 兰州 730050)
三阶微分方程起源于应用数学和物理学的各种不同领域中,例如,带有固定或变化横截面的屈曲梁的挠度、三层梁、电磁波、地球引力吹积的涨潮等[1],因此,对于其正解的理论研究在实际问题中就显得格外重要。近年来,关于三阶微分方程边值问题的研究已经有了很多的成果[2-9]。
Li[10]运用不动点指数理论证明了四阶周期边值问题
(1)
正解的存在性,其中:f∈C([0,1]×[0,+∞),[0,+∞));α,β∈R且满足0<α<(β/2+2π2)2,β>-2π2;α/π4+β/π2+1>0。
受以上文献的启发,我们的主要目的是研究三阶周期边值问题
(2)
正解的存在性,其中:f∈C([0,2π]×[0,+∞),[0,+∞));a,b,c∈R且满足
(3)
为方便起见,我们引入以下记号:
研究的主要结果如下:
定理1设f∈C([0,2π]×[0,+∞),[0,+∞)),且式(3)成立,则在下列每一种情形下:
周期边值问题(2)至少有一个正解。
从定理1中我们能得到以下推论:
推论1设f∈C([0,2π]×[0,+∞),[0,+∞)),且式(3)成立,则在下列每一种情形下:


周期边值问题(2)有一个正解。
注记1注意到-a(b2+c2)是线性特征值问题
的一个特征值,如果定理1的(ⅰ)或(ⅱ)中的一个不等式不成立,那么将不能保证周期边值问题(2)解的存在性。
1 预备引理
我们考虑一般的线性边值问题
其中:n≥2;ai,μ∈R;h∈C[0,2π]。我们有以下的引理[11]:
引理1若线性边值问题
(5)
有唯一解rn(t)∈C∞[0,2π],则线性问题(4)有唯一解u∈Cn[0,2π],它的表达式为

其中:
引理2设a,b,c∈R且a≠0,b≠0,c≠0,则三阶线性问题
(6)
的唯一解为

t∈[0,2π]
其中:
p=(e2πb-1)2+2e2πb(1-cos(2πc))。
证明由于三阶线性问题(6)中微分方程的特征根为a和b±ic,则线性问题(6)的通解为
r3(t)=c1eat+c2ebtcos(ct)+c3ebtsin(ct),
t∈[0,2π]
经过计算得
通过化简整理可得到r3(t)的表达式。
引理3设a,b,c∈R且式(3)成立,则对任意的t∈[0,2π],r3(t)>0。

1-e2πa>0,a-b<0,p>0,
经过简单的推导得
e2πbsin(c(2π-t))+sin(ct)<0,
cos(ct)-e2πbcos(c(2π-t))<0,t∈[0,2π]
所以,对任意的t∈[0,2π],r3(t)>0。
假设式(3)在文章的剩余部分都成立,由引理3可得,对任意的t∈[0,2π],有r3(t)>0。令m=mint∈[0,2π]r3(t),M=maxt∈[0,2π]r3(t),则对任意的t∈[0,2π],有0 m≤G3(t,s)≤M,t,s∈[0,2π]。 (7) 令h∈C[0,2π]。由引理1,线性周期边值问题 有唯一解u,它的表达式为 现在我们定义一个算子A:C+[0,2π]→C+[0,2π]为 (8) 其中:C+[0,2π]是C[0,2π]中所有非负函数构成的锥,则周期边值问题(2)的解等价于A的不动点,我们将运用锥上的不动点指数理论找到A的非零不动点。选择C+[0,2π]中的子锥 K={u∈C+[0,2π]|u(t)≥σ‖u‖,0≤t≤2π}, 其中:σ=m/M>0,‖u‖是C+[0,2π]中的最大范数,则我们有以下引理: 引理4A(K)⊂K且A:K→K是全连续的。 证明设u∈K,由式(7)后面的不等式可得 因此 再由式(7)前面的不等式得 这表明Au∈K,因此A(K)⊂K。A的全连续性是显然的。 对r>0,令Kr={u∈K|‖u‖ 引理5设A:K→K是全连续算子,若对任意的u∈∂Kr和0<μ≤1,有μAu≠u,则i(A,Kr,K)=1。 引理6设A:K→K是全连续算子,若满足以下2个条件: (ⅰ) infu∈∂Kr‖Au‖>0; (ⅱ) 对任意的u∈∂Kr和μ≥1,有μAu≠u,则i(A,Kr,K)=0。 定理1的证明由引理4和K的定义得,式(8)定义的算子A的非零不动点是周期边值问题(2)的正解,我们分2种情况证明A有一个非零不动点。 f(t,u)≤[-a(b2+c2)-ε]u,∀t∈[0,2π], 0≤u≤r0。 (9) 令r∈(0,r0),要证明对任意的u∈∂Kr和0<μ≤1,有μAu≠u,用反证法,即存在u0∈∂Kr和0<μ0≤1,使得μ0Au0=u0,则由A的定义得u0(t)满足微分方程 u‴0(t)-(a+2b)u″0(t)+(b2+c2+2ab)u0′(t)- a(b2+c2)u0(t)=μ0f(t,u0(t)), t∈[0,2π] (10) 和边界条件,对方程从0到2π上积分,并且利用u0(t)的周期性和式(9),可得 i(A,Kr,K)=1。 (11) f(t,u)≥[-a(b2+c2)+ε]u,∀t∈[0,2π], u≥H。 (12) 令 C=max0≤t≤2π,0≤u≤H|f(t,u)- [-a(b2+c2)+ε]u|+1, 则可得 f(t,u)≥[-a(b2+c2)+ε]u-C, ∀t∈[0,2π],u≥0。 (13) 取R>R0∶=max{H/σ,r0},设u∈∂KR。由于对s∈[0,2π],有u(s)≥σ‖u‖>H,结合式(7)、式(12)和K的定义可得 2πm[-a(b2+c2)+ε]σ‖u‖, 即 ‖Au‖≥2πm[-a(b2+c2)+ε]σ‖u‖。 (14) 因此infu∈∂KR‖Au‖>0,即引理6的(ⅰ)成立。下面证明若R足够大,则对任意的u∈∂KR和μ≥1,有μAu≠u,用反证法,即存在u0∈∂KR和μ0≥1,使得μ0Au0=u0,则u0(t)满足微分方程(10)和边界条件,对方程(10)从0到2π上积分得 因此 (15) (16) i(A,KR,K)=0。 (17) 再由不动点指数的可加性、式(11)和式(17)可得 i(A,Kr,K)=-1。 f(t,u)≥[-a(b2+c2)+ε]u, ∀t∈[0,2π],0≤u≤η。 (18) 令r∈(0,η),则对任意的u∈∂Kr,由式(14)得infu∈∂Kr‖Au‖>0,即引理6的条件(ⅰ)成立。下面证明对任意的u∈∂Kr和μ≥1,有μAu≠u,用反证法,即存在u0∈∂Kr和μ0≥1,使得μ0Au0=u0,则u0(t)满足微分方程(10)和边界条件,由式(10)和式(18)可得 i(A,Kr,K)=0。 (19) f(t,u)≤[-a(b2+c2)-ε]u,∀t∈[0,2π],u≥H。 令 C=max0≤t≤2π,0≤u≤H|f(t,u)- [-a(b2+c2)-ε]u|+1, 则可得 f(t,u)≤[-a(b2+c2)-ε]u+C, ∀t∈[0,2π],u≥0。 (20) 要证明对任意的u∈∂KR和0<μ≤1,有μAu≠u,用反证法,即存在u0∈∂KR和0<μ0≤1,使得μ0Au0=u0,则u0(t)满足微分方程(10)和边界条件,由式(10)和式(20)可得 i(A,KR,K)=1。 (21) 再由不动点指数的可加性、式(19)和式(21)得到






2 主要结果的证明