Koch曲线的Hausdorff测度的改进下界估计∗

郭 东 亮

(中山大学电子与通信工程学院，广东 广州 510006)

0 引 言

在分形几何研究中，确定分形的Hausdorff维数与Hausdorff测度非常重要，但这又是一个难题，相对而言，计算Hausdorff测度更困难[1].对于一般集合，计算其Hausdorff测度难度很大，尚无普遍适用的计算方法.满足开集条件的自相似分形集由于具有严格的自相似性，目前已知的研究成果最多.Cantor集、Koch曲线和Sierpinski垫片是3个经典自相似集，目前三分Cantor集的Hausdorff维数与Hausdorff测度已经解决[1]，但对于Koch曲线和Sierpinski垫片，人们只算得其Hausdorff维数，对于其Hausdorff测度则难以计算出准确值，只能估计其上下界[2].

文献[3-5]研究了Koch曲线K的Hausdorff测度并对其上界进行了估计，文献[6-8]利用质量分布原理得出了K的Hausdorff测度的下界估计值Hs(K)≥0.526 316；文献[9-10]用数值计算方法对K的Hausdorff测度进行了计算机模拟并得到了数值解.本文在已有研究成果基础上，通过定义质量分布函数μ，对任意覆盖U导出了关系式μ(U)≤1.876|U|s，基于该式并利用质量分布原理得出了Koch曲线Hausdorff测度的更好下界估计.

1 Koch曲线及其Hausdorff测度

1.1 Koch曲线

设K0是Euclid平面R2上的线段[0，1]，将K03等分，以中间的1/3线段为底边向上作正三角形，再去除底边，得到一条由4个长度为1/3的边组成的折线，记为K1，对K1的每个边重复上述过程，得到42个长度为1/32的边组成的折线，记为K2，无限重复以上过程，得到折线序列K0，K1，K2，…，Kn，…，当n→∞时，此折线序列趋于一条曲线K，即Koch曲线.

下面是关于Koch曲线K的一些相关定义和结果[1-2].

(1)K是由压缩比为1/3的相似压缩定义的，其Hausdorff维数是s=log34.

(2)K是路径连通的，设点A、A′∈K，记AA′为K上的从点A到点A′的连通弧.

1.2 相关定义和引理

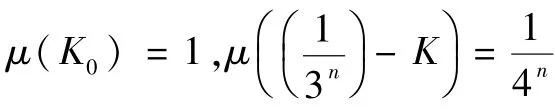
定义2第n级Koch曲线Kn含有4n个底边长为1/3n的等腰三角形，每个这样的等腰三角形称为一个基本三角形，记为△n，Kn中与覆盖U相交的△n的个数记为α(U).

引理1(质量分布原理)[1]设任意非空紧集F⊂Rn，μ是F上定义的质量分布，且对某个s存在c＞0和δ＞0，使

μ(U)≤c|U|s

对所有满足|U|≤δ的集U成立，则F的Hausdorff测度

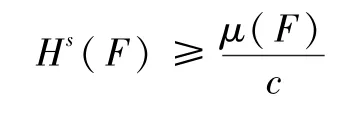
2 主要结果及证明

定理1记K为Koch曲线，U为K的任意覆盖，则有

证明分别分析α(U)的可能情况.对于α(U)=2的情况，所有覆盖类型可以归结为4种，如图1所示.注:为表达简便，本文只画出各等腰三角形的底边，以下同).

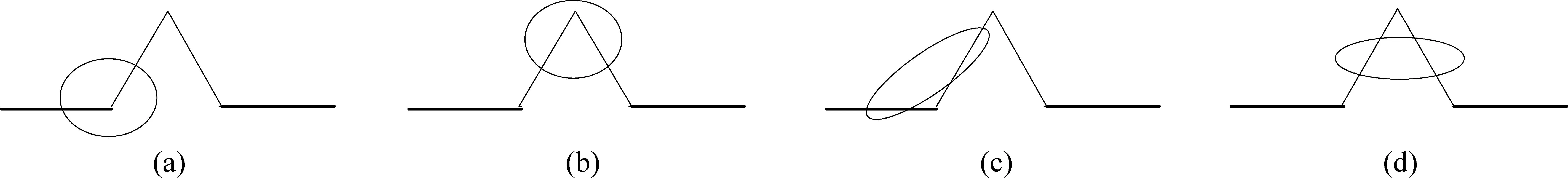
图1 第1种情况(α(U)=2)

图1中，(a)和(c)都是U覆盖K1的第1个和第2个三角形的情况，其中(a)代表U的边界与K1相交只有2个交点的情况，(c)代表U的边界与覆盖K1相交有≥3个交点的情况；(b)和(d)都是U覆盖K1的第2个和第3个三角形的情况，其中(b)代表U与覆盖K1的交点数为2的情况，(d)代表U与覆盖K1的交点数≥3的情况.

α(U)=3、4的情况分别示于图2、3，且根据交点数量情况分别示于(a)和(b)图.

图2 第2种情况(α(U)=3)

图3 第3种情况(α(U)=4)

最后分析α(U)=1的情况，图4示出其覆盖类型的几种情况，对于图4(a)的情况，由于分形迭代过程的无限性和分形的自相似性，图4(a)的下一步迭代将出现图1(a)的情况，即α(U)=2的情况.同理，图4(b)的下一步迭代将出现图2(a)的情况，即α(U)=3的情况；图4(c)的下一步迭代将出现图3(a)的情况，即α(U)=4的情况.此外，根据覆盖U的位置和形状，也可能出现图1(c)、图2(b)、图3(b)的情况，不再赘述.

综上，由于分形迭代的无限性和分形的自相似性，仅需考虑α(U)=2，3，4 3种情况(由平面几何关系，α(U)≥5的情况并不存在).

选取Kn，n=3的情况讨论，如图5.对于第1种情况的(a)，称U的边界与Kn相交的2个交点中，左边的交点为左交点，记为L，右边的交点为右交点，记为R.

当L在线段D3E上时，根据R的位置分别分析如下:

(1)当R在线段EE2、E2E1、E1E3和E3F内时.

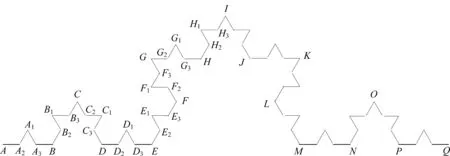
图5 Koch曲线(K3)

这种情况是L落在△DD1E内(指该三角形所包含的线段DD2、D2D1、D1D3和D3E内)且R落在△EE1F内(指该三角形所包含的线段EE2、E2E1、E1E3和E3F内)，根据分形的自相似性，这种情况不需单独考虑.

(2)当R在线段FF2和F2F1内时.

对任意覆盖U和Kn(n可为任意大)，都有

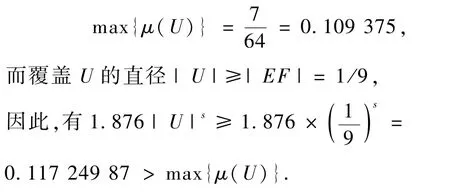
(3)当R在线段F1F3和F3G内时.

对任意覆盖U和Kn(n可为任意大)，都有

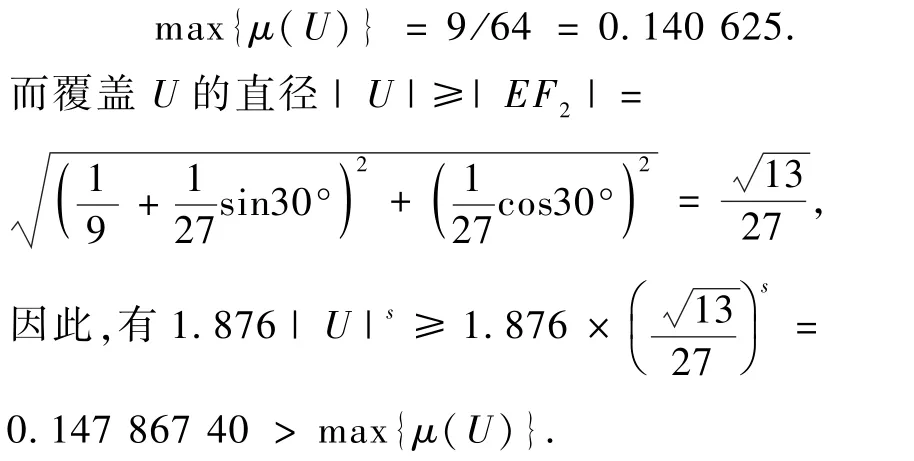
(4)当R在线段GG2、G2G1、G1G3、G3H、HH2、H2H1内时.

对任意覆盖U和Kn(n可为任意大)，都有

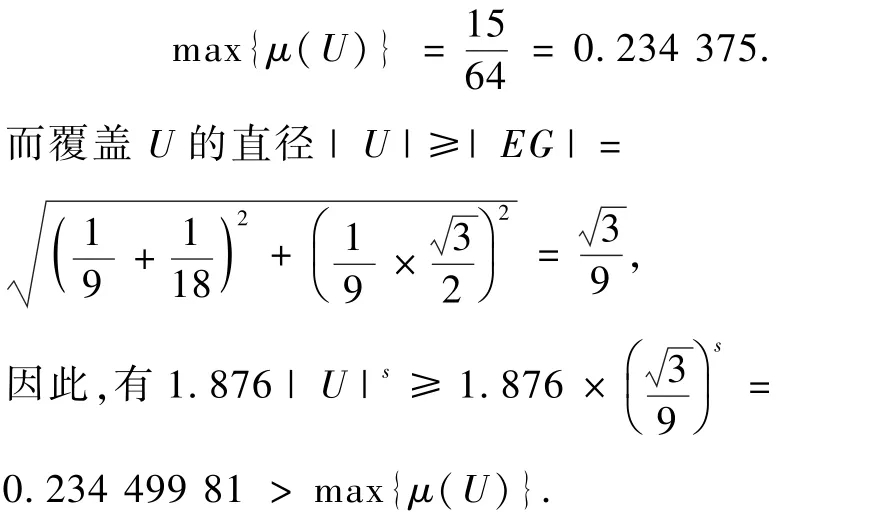
(5)当R在线段H1H3、H3I内时.

对任意覆盖U和Kn(n可为任意大)，都有

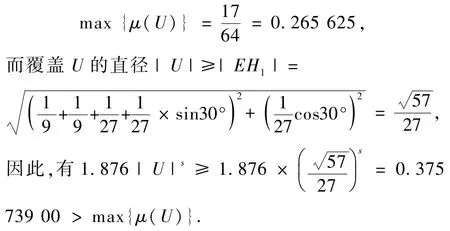
综上，对于Kn，不管n多大，只要覆盖U满足:L在线段D3E上，R在多边形FF1GG1HH1I所对应的Koch曲线内，式(1)恒成立.

同理，可以得到对任意的n，当L分别在线段D3D1、D1D2、D2D、DC3、C3C1、C1C2、C2C、CB3、B3B1、B1B2、B2B、BA3、A3A1、A1A2、A2A上，R在多边形FF1GG1HH1I所对应的Koch曲线内时，式(1)恒成立.

用同样的方法，可以得到对于第2、3种情况，式(1)也成立.

定理1证毕.

利用质量分布原理，可立刻得到Koch曲线K的Hausdorff测度的下界估计.

定理2记Koch曲线K的Hausdorff测度为Hs(K)，则有

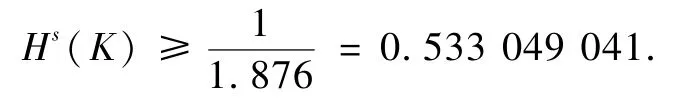
这是Koch曲线Hausdorff测度目前已知的最好下界.

3 结 论

本文通过在Koch曲线K上定义质量分布函数μ，导出对K的任意覆盖U的关系式μ(U)≤1.876|U|s，利用质量分布原理计算出了K的Hausdorff测度的新下界估计值Hs(K)≥0.533 049 041，这是关于Koch曲线Hausdorff测度下界的更好估计，也是目前已知的最好下界.