基于广义Kelvin模型的非定常盐岩蠕变模型
韩伟民,闫怡飞,闫相祯
(1.中国石油大学(华东)储运与建筑工程学院,山东青岛,266580;2.中国石油大学(华东)机电工程学院,山东青岛,266580)
四川盆地作为油气资源的重要赋存地,分布着大量厚度不一的盐岩地层。而位于川东北三叠系嘉陵江组盐岩地层的多口油气田生产井出现了套管变形损坏情况[1],因此,研究该地层段盐岩的流变特性就显得尤为重要。当应力水平低于岩石长期强度时,其蠕变曲线仅存在衰减蠕变阶段和稳态蠕变阶段;当应力水平高于岩石长期强度时,其蠕变曲线呈现完整的3个阶段,即衰减蠕变阶段、稳态蠕变阶段和加速蠕变阶段。室内试验结果表明盐岩的蠕变曲线也存在上述3个阶段[2],但对于工程问题而言,处于高应力状态下的深层盐岩体蠕变过程中并不会进入加速蠕变阶段而发生损伤破坏,因此,研究衰减蠕变阶段和稳态蠕变阶段盐岩的非线性蠕变特征对工程实际更有意义。其中,衰减蠕变阶段的存在时间相对短暂,在恒定载荷作用下稳态蠕变阶段则更为持久。国内外学者针对盐岩的蠕变特征开展了大量研究[3-6],但由于地质环境、矿物成分及含水率等影响因素的存在,不同地区的盐岩弹性参数及流变特性存在明显差异,因此,单一的蠕变本构模型形式并不具有普适性。目前针对盐岩的非线性流变问题,主要有以下几种常见研究方法[7]:1)以组合的黏弹性或黏塑性元件模型为基础,在其后串联加入非线性元件,蠕变参数可根据室内试验结果来确定。刘开云等[8]将Maxwell模型与非线性黏塑性体串联组成新的非线性黏塑性模型以描述泥岩的蠕变过程。一般的工程问题可采用该方法进行近似处理,但对于复杂的岩石蠕变本构,组合的黏弹性或黏塑性元件模型并不能反映与蠕变时间和应力水平相关的非线性蠕变特征,此时,该方法的近似处理结果并不适用。2)将元件模型中的线性元件视为时间的函数,并以非线性元件进行替代,改进后的非线性元件组合模型的蠕变参数可根据室内试验结果进行确定。王军保等[9-10]用非线性黏壶代替常规Burgers模型的线性黏壶,通过考虑损伤因子和蠕变对黏滞系数的影响等,建立了改进的非线性元件组合模型以描述盐岩的非线性蠕变特性。ZHOU等[11-12]用分数阶Abel黏壶元件替代西原模型的线性黏壶,建立了改进的西原模型以反映盐岩流变的3个阶段。该方法虽较为理想,但模型中蠕变参数辨识的计算处理相对繁琐和困难,且改进后的非线性元件模型并不能反映温度因素对岩石蠕变过程的影响。3)基于室内试验结果,考虑损伤和断裂力学,建立经验本构关系式。高小平等[13]应用不同应力和温度条件下的盐岩变形机制,得到了盐岩的稳态蠕变应变率与偏应力、能量与温度之间的函数关系式。杨春和等[14-15]通过不同应力水平作用下盐岩蠕变变形与时间的关系,建立了盐岩瞬态与稳态蠕变的耦合本构方程。王安明等[16-17]采用Norton Power盐岩蠕变本构模型分别对盐穴储气库及盐岩井段井眼缩径进行了计算分析。该方法可充分利用试验数据进行回归分析得到较为可靠的本构关系式,但由于岩石取芯费用较高且室内蠕变时间较长,短期内较难获得大量可靠的室内试验数据。鉴于此,为了避免上述几种非线性蠕变模型构建方法的局限性,根据川东北油气田盐岩三轴蠕变试验结果,并参考其他学者在研究盐岩蠕变特性中采用的方法[7,10-12,18],本文作者将改进后的非线性元件组合模型与非线性元件进行串联,构建新的适用于川东北油气田嘉陵江组盐岩的非线性蠕变本构模型,以便能够更好地描述蠕变时间、温度和应力水平对盐岩衰减蠕变阶段和稳态蠕变阶段的非线性蠕变特征的影响。首先,在广义Kelvin模型的基础上用非定常黏壶替代线性黏壶构建非定常广义Kelvin模型,将其与能够描述盐岩稳态蠕变特征的Heard模型进行串联组合,构建新的NGKH非线性盐岩蠕变模型,以描述盐岩的瞬态蠕变和稳态蠕变过程;然后,基于套损现象集中发生的嘉陵江组盐岩地层的岩心室内蠕变试验结果,采用Levenberg-Marquardt算法分别对不同应力水平下的NGKH模型、非定常广义Kelvin模型和广义Kelvin模型参数进行辨识,通过比较验证新模型的适用性;最后,基于FLAC3D提供的接口程序对NGKH模型进行二次开发,并通过数值试验对其正确性进行验证。
1 盐岩蠕变本构模型
1.1 非定常广义Kelvin模型的构建
广义Kelvin模型是由胡克体与Kelvin模型串联而成,如图1所示。

图1 广义Kelvin模型Fig.1 Generalized Kelvin model
广义Kelvin模型的蠕变方程为[18]:

式中:E0为串联胡克体的弹性模量;E1为Kelvin体的黏弹性模量;η1为Kelvin体的初始黏滞系数。
由于广义Kelvin模型只能描述岩石的线性蠕变特征,对于蠕变特性复杂的盐岩来说并不适用。将Kelvin体中牛顿黏壶的黏滞系数视为时间的函数,建立非定常黏壶[19]:
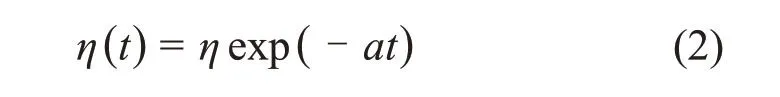
式中:η(t)为非定常黏壶的黏滞系数;a为待定系数。
对式(2)求导可得
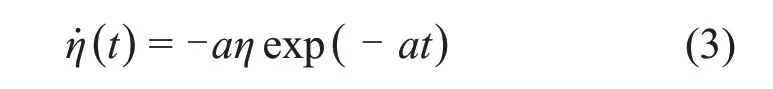
由式(3)可知:当a>0时,˙(t)≤0,黏滞系数随时间衰减;当a=0时,η(t)=η,非定常黏壶退化为线性黏壶;当a<0时,˙(t)≥0,黏滞系数随时间增大。因此,可通过变化a来实现非定常Kelvin体的非线性蠕变特征。用上述非定常黏壶替换图1中广义Kelvin模型的线性黏壶,构建而成的非定常广义Kelvin蠕变模型如图2所示。

图2 非定常广义Kelvin模型Fig.2 Non-stationary generalized Kelvin model
非定常Kelvin体的状态方程为

式中:˙为蠕变速率。
分离变量求定积分,并由ε=J(t)σ可得其蠕变柔量JK为
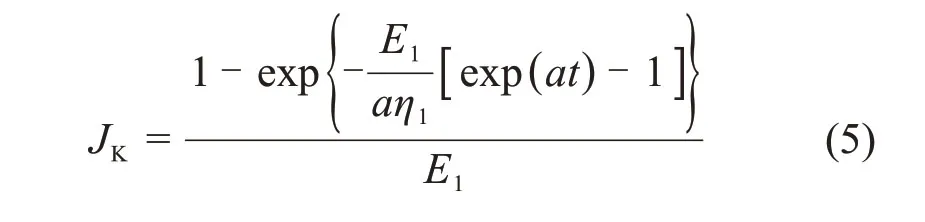
由式(1)和式(5)可得非定常广义Kelvin模型的蠕变柔量为

则非定常广义Kelvin模型的一维本构方程为
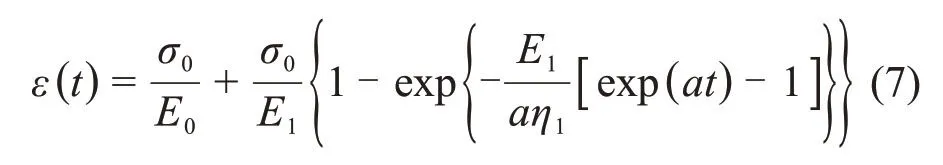
在三维应力状态下,岩石的应力张量可分解为偏应力张量Sij和球应力张量σm。通常考虑应力偏量仅引起蠕变变形,球应力引起弹性变形,同时假定岩石为各向同性体,由式(1)可得广义Kelvin模型的三维蠕变方程为[19]
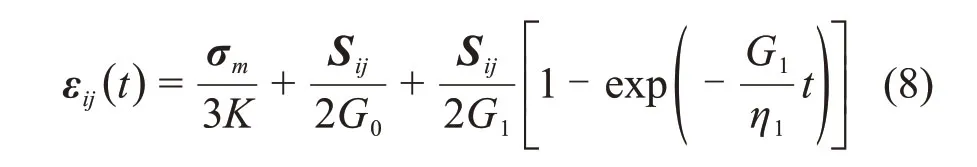
式中:εij为应变张量;K和G0分别为串联胡克体的体积模量和剪切模量;G1为Kelvin体的剪切模量。
在等围压三轴压缩试验中σ2=σ3,代入式(8)可得常规三轴压缩试验中广义Kelvin模型的轴向应变方程:
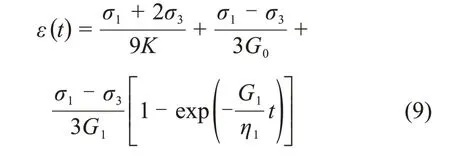
同理,由式(7)和式(8)可得非定常广义Kelvin模型的三维蠕变方程和轴向应变方程分别为[19]:
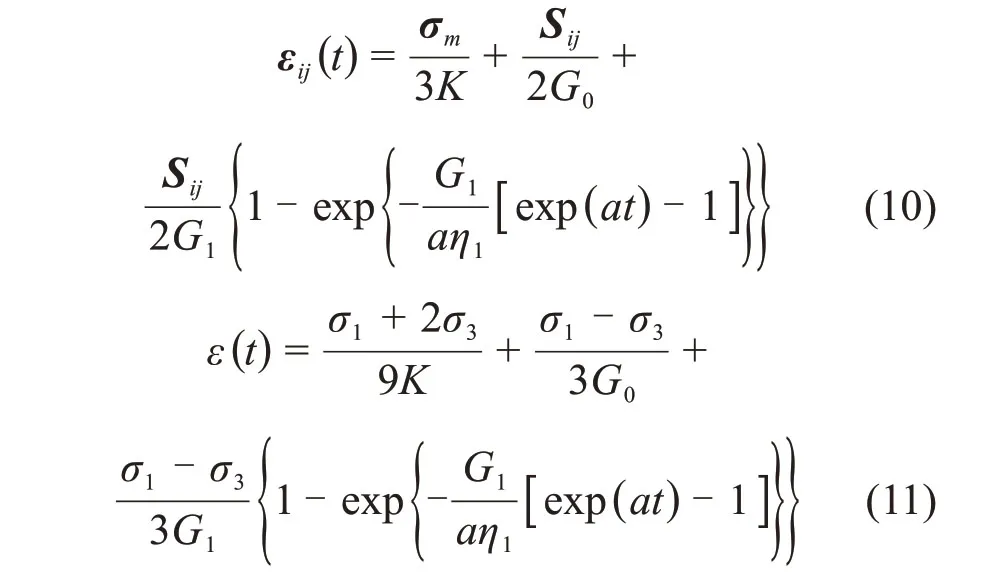
1.2 Heard模型的构建
研究盐岩的稳态蠕变本构方程即确定其稳态蠕变速率与温度、偏应力之间的变化关系,盐岩的蠕变机制和蠕变本构方程随其所处地质环境的不同而变化[20]。对于川东北油气田的深部盐岩地层来说,其蠕变机制属于位错滑移机制[6],符合Heard本构模型,本构方程如式(12)所示。曾德智等[21-22]利用Heard蠕变模型对盐岩地层套管蠕变外载、盐岩层井壁稳定性及井眼缩径量进行了计算分析;LI等[6]通过对盐岩和盐膏岩进行的室内三轴蠕变试验,分析了不同矿物成分和围压对盐岩蠕变速率的影响,并采用Heard模型对试验结果进行了拟合。

式中:为稳态蠕变速率;Q为激活能;R为摩尔气体常量,R=8.314 J/(mol·K);σ为偏应力;T为热力学温度,K;A和B为流变常数。
按照GB/T 50266—2013“工程岩体试验方法标准”,将取自川东北某气田嘉陵江组地层埋深3 838~3 858 m处的岩石岩芯,加工成高为100mm、直径为50mm的标准圆柱体岩石试样共2组。该地层段盐岩层厚度为174m,地层岩性以灰白色硬石膏岩、白色盐岩、灰白色膏盐岩为主,夹灰色灰质白云岩、深灰色、灰色白云岩、膏质灰岩、泥灰岩。本试验采用MTS材料试验机进行,该装置由轴向加压、侧向加压、温控设备和微机系统组成。对第一组岩石试样,在室温条件下将围压加载到15MPa并保持不变,轴向采用单级加载方式分别施加30,35,40和45MPa的均布载荷并保持不变,加载时间持续40 h左右。由前人研究成果可知:温度因素对盐岩的蠕变特性影响非常显著,因此,对于第二组岩石试样,首先将三轴室的温度分别加到50℃和100℃并保持3 h左右,再将围压加载至15MPa并保持不变,轴向仍然采用单级加载方式施加30MPa均布载荷并保持不变,加载时间持续30 h左右。图3(a)和图3(b)所示分别为围压15MPa时,不同偏应力及不同温度下的盐岩应变-时间曲线。基于Heard蠕变模型,采用Origin分析软件对图3中不同条件下的稳态蠕变率进行非线性拟合,得到的参数A,B和Q见表1。
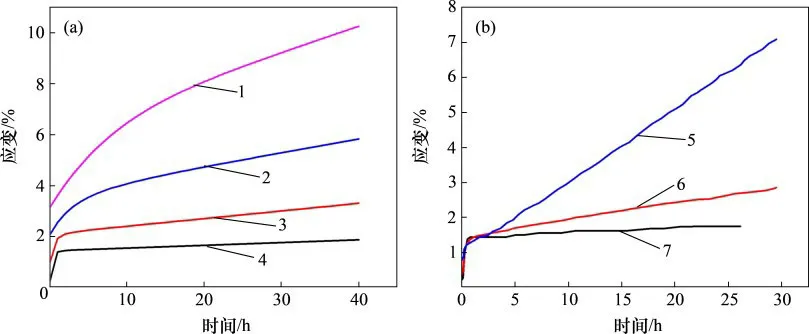
图3 盐岩室内试验蠕变曲线Fig.3 Creep curves of salt rock

表1 拟合得到的Heard模型蠕变参数Table1 Creep parameters of fitted Heard model
1.3 NGKH模型的构建
王军保等[18]基于芒硝的室内三轴蠕变压缩试验,将分数阶广义Kelvin模型与未考虑温度因素的Heard模型相结合,构建了能够反映芒硝非线性蠕变特性的蠕变本构模型。而在不同地层深度和地层温度下,盐岩的蠕变过程受温度影响较为显著,因此,本文采用的Heard模型中仍然考虑温度影响因素。
上述建立的非定常广义Kelvin模型能够描述盐岩的瞬时变形及衰减蠕变状态,而Heard蠕变模型能够反映盐岩的偏应力、温度与稳态蠕变速率的关系,因此,参考岩石非线性蠕变模型的经典构建思路,将非定常广义Kelvin模型与Heard蠕变模型进行串联,构成新的盐岩非线性蠕变模型,简称NGKH蠕变模型(见图4),下式即为NGKH蠕变模型的轴向应变方程:

式(13)中第1项和第2项反映初始蠕变阶段的瞬时应变,第3项反映衰减蠕变阶段的黏弹性应变,第4项反映稳态蠕变阶段的黏性流动应变。

图4 NGKH蠕变模型Fig.4 NGKH creep model
1.4 蠕变参数敏感性分析
在应力状态、温度相同的条件下,对式(13)中的待定系数a和A进行敏感性分析,图5(a)和图5(b)所示分别为系数a和A对NGKH模型蠕变曲线的影响。对式(3)进行分析可知a的变化能改变Kelvin体中非线性黏壶的蠕变性质。由图5(a)可以看出a的变化对蠕变曲线的形状尤其是衰减蠕变阶段影响较为显著:当a>0时,随着a增大,衰减蠕变阶段的蠕变速率衰减速度加快,进入稳态蠕变阶段的时间提前,此后各蠕变曲线几乎重合;当a<0时,随着a减小,衰减蠕变阶段的蠕变速率衰减速度同样加快,进入稳态蠕变阶段的时间同样提前,但此后各蠕变曲线近似平行,轴向应变呈近似线性减小。从图5(b)可知:A的变化主要影响稳态蠕变阶段的曲线形态,对衰减蠕变阶段则影响很小。随着A增大,稳态蠕变率明显增大,轴向应变也明显增大。蠕变参数B对蠕变曲线的影响规律与A的影响规律相似。

图5 蠕变参数a和A对NGKH模型蠕变曲线的影响Fig.5 Influence of parameters a and A on creep curves of NGKH model
将围压固定为15MPa,在其他蠕变参数不变的情况下,分别观察应力σ1的变化对NGKH模型及广义Kelvin模型蠕变曲线的影响,如图6所示。
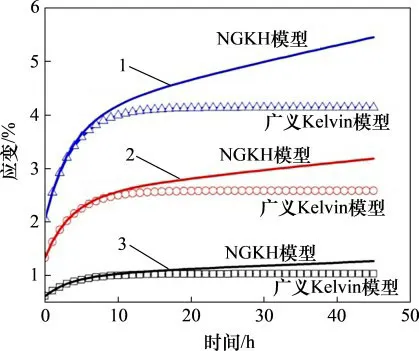
图6 轴向载荷对NGKH模型和广义Kelvin模型蠕变曲线的影响Fig.6 Effect of axial load on creep curves of NGKH model and generalized Kelvin model
从图6可以看出:随着轴向载荷增大,NGKH模型及广义Kelvin模型的轴向应变均随之增大,但广义Kelvin模型的蠕变曲线呈线性变化,而NGKH模型的稳态蠕变速率和蠕变曲线均呈非线性变化。因此,在不同应力状态下,盐岩的蠕变曲线形态可通过变化NGKH模型中a,A和B来调整,使NGKH模型更加适用于岩石的流变分析。
2 蠕变模型参数辨识
针对本文提出的NGKH蠕变模型,式(13)中需要给出的参数分别是K,G0,G1,a,η1,A,B和Q,其中A,B和Q已经通过室内蠕变试验曲线拟合分析确定。令A1=(σ1+2σ3)/(9K)+(σ1-σ3)/(3G0),再利用K,G0与弹性模量E0和泊松比λ0之间的关系求得E0,进而反求出K和G0,此时,需要拟合确定的参数变为A1,G1,a和η1。根据图3中不同应力状态下盐岩室内三轴蠕变试验结果,运用Origin分析软件的Levenberg-Marquardt算法[23],通过自定义函数模型,对A1,G1,a和η1进行辨识。表2、表3和表4所示分别为NGKH模型、非定常广义Kelvin模型和广义Kelvin模型的蠕变参数辨识结果。将拟合得到的各模型蠕变曲线与室内试验结果进行对比,如图7所示。其中图7(a)~7(d)所示分别为不同偏应力下的蠕变曲线对比,图7(a)、图7(e)和图7(f)所示分别为不同温度下的蠕变曲线对比。从表2~4可见:在相同应力状态下,不同蠕变模型的K、G0和G1较为接近,而a和η1却存在明显差异。从图7(a)和图7(b)可知:a和η1组成的非定常黏壶对衰减蠕变阶段起着控制作用,而Heard体的加入直接影响了稳态蠕变阶段的蠕变曲线走向,同时反映出NGKH模型的灵活性和适用性。
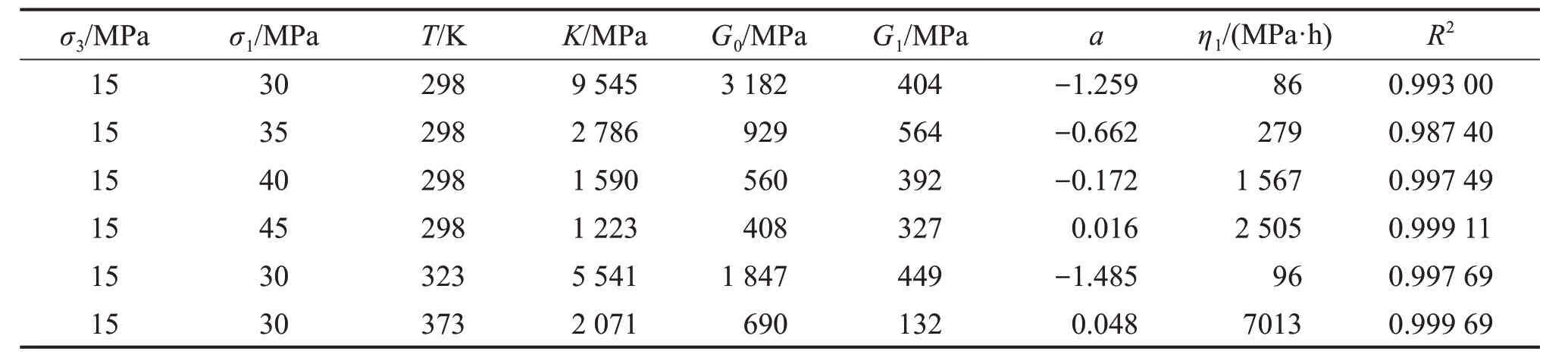
表2 NGKH模型蠕变参数辨识Table2 Creep parameters identification for NGKH model
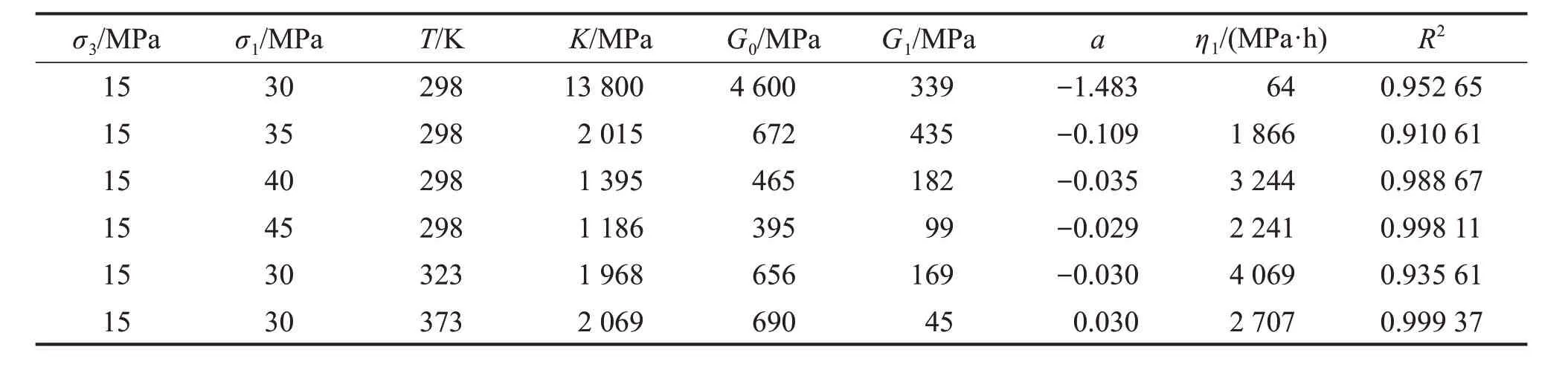
表3 非定常广义Kelvin模型参数辨识Table3 Creep parameters identification for non-stationary generalized Kelvin model
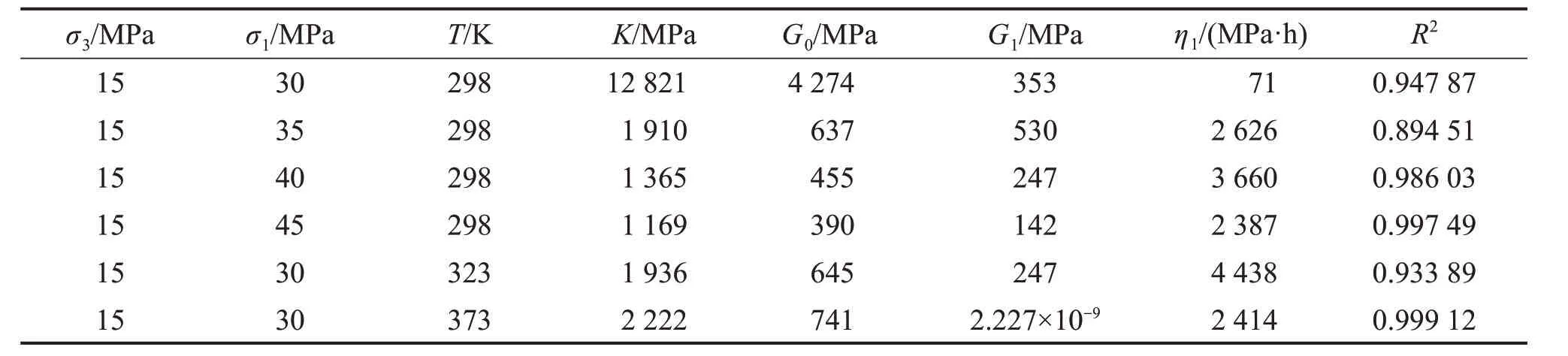
表4 广义Kelvin模型参数辨识Table4 Creep parameters identification for generalized Kelvin model
从图7可知:与非定常广义Kelvin模型及常规广义Kelvin模型相比,由于引入了非定常黏壶及Heard蠕变体,本文提出的NGKH模型的拟合效果相对较好,理论计算结果与室内试验结果吻合度明显更高,能够较好地对不同应力状态下盐岩的瞬时应变、瞬态蠕变阶段和稳态蠕变阶段进行描述,更能反映盐岩的非线性蠕变特征,由此验证了该模型的合理性和可靠性。
3 蠕变模型二次开发
FLAC3D软件内置的蠕变模型均有特定的使用范围,在一定程度上影响了FLAC3D的广泛应用[24]。因此,部分学者利用其提供的接口程序对新的蠕变模型进行了二次开发,例如熊良宵等[25-27]就基于FLAC3D分别对改进Burgers模型和河海模型进行了二次开发。为了能够将本文提出的NGKH蠕变模型程序化,首先将其本构方程改写成三维差分形式。
3.1 NGKH模型的有限差分形式
3.1.1 模型各部分的偏应力与偏应变关系式
由图4和式(13)可知:NGKH模型各部分之间为串联关系,因此应力相等,应变相加,则有[24,28]
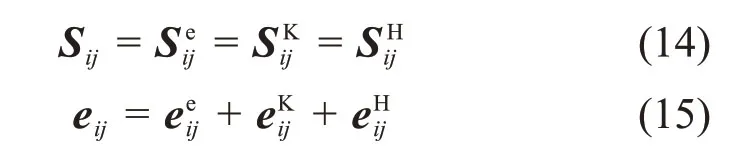
对于串联弹簧胡克体,偏应力与偏应变速率的关系为

对于非定常Kelvin体,偏应力Sij和偏应变有如下关系[28]:

式中:为非定常Kelvin体的黏滞系数,且
对于串联Heard体,有
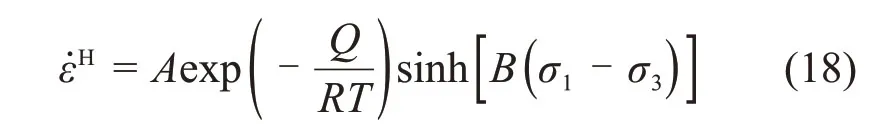
引入应力强度q,且q=在FLAC3D中可通过相应指针读取应力张量的各分量,然后求出q。由经典弹塑性力学可知因此,对于Heard体,偏应力Sij与偏应变速率之间的关系为

3.1.2 模型各部分的增量形式
为了利用FLAC3D软件进行二次开发,将NGKH本构方程的上述内容改写成有限差分形式。将式(15)写成增量形式:
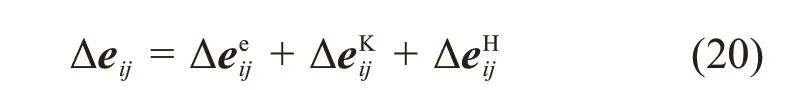
式(16)的增量形式可写为
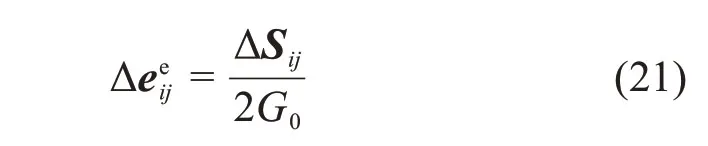
将式(17)写成增量形式:

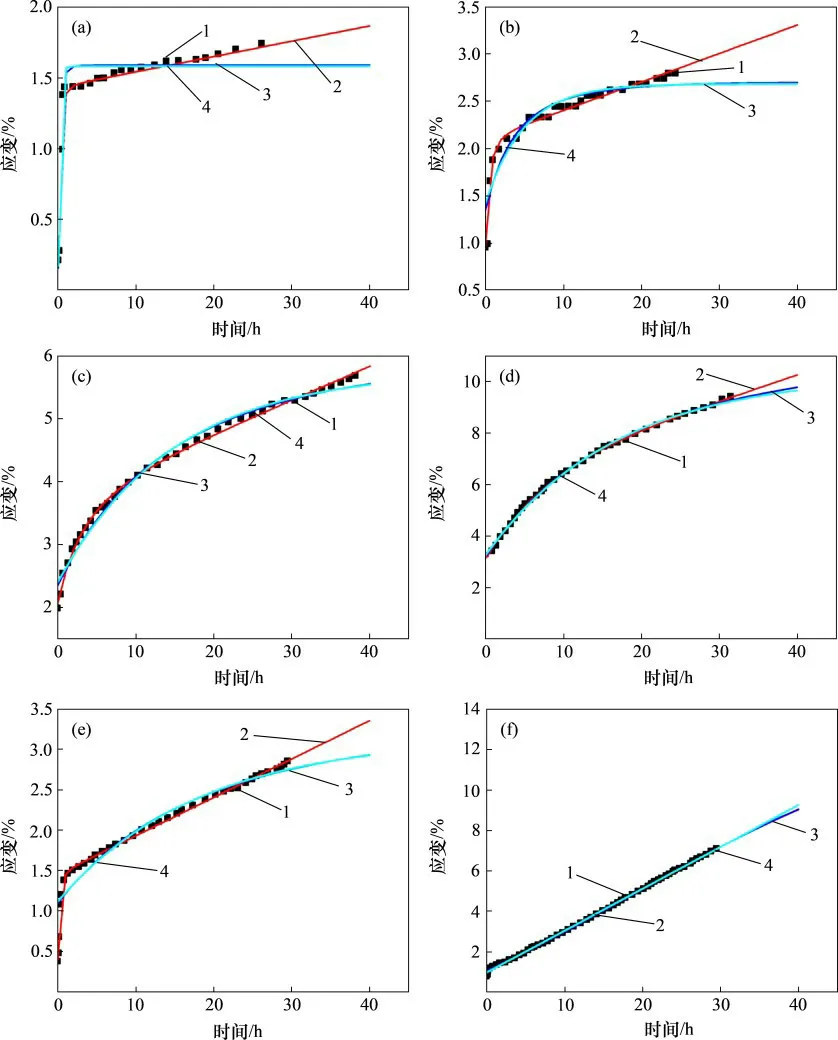
图7 NGKH模型、非定常广义Kelvin模型和广义Kelvin模型拟合曲线对比Fig.7 Comparison of fitting curves of NGKH model,non-stationary generalized Kelvin model and generalized Kelvin model
将式(22)整理后,得到非定常Kelvin体第i步偏应变更新公式为
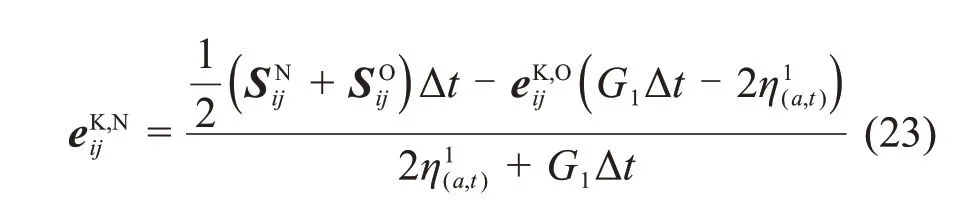
将式(23)进一步整理后可得:


式中:γ为蠕变乘子,随应力和蠕变应变的变化而变化。
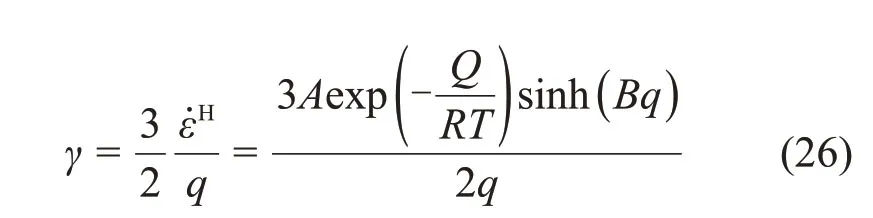
由此式(19)的增量形式可写为
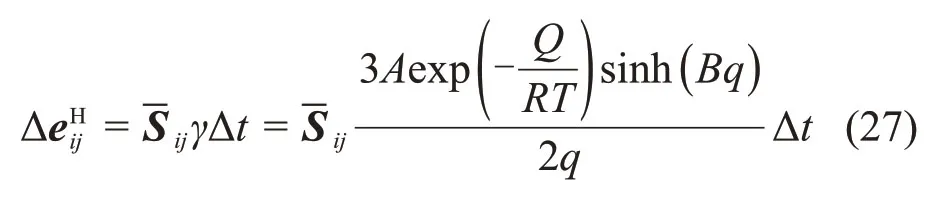
将式(21)、式(24)和式(27)代入式(20),有
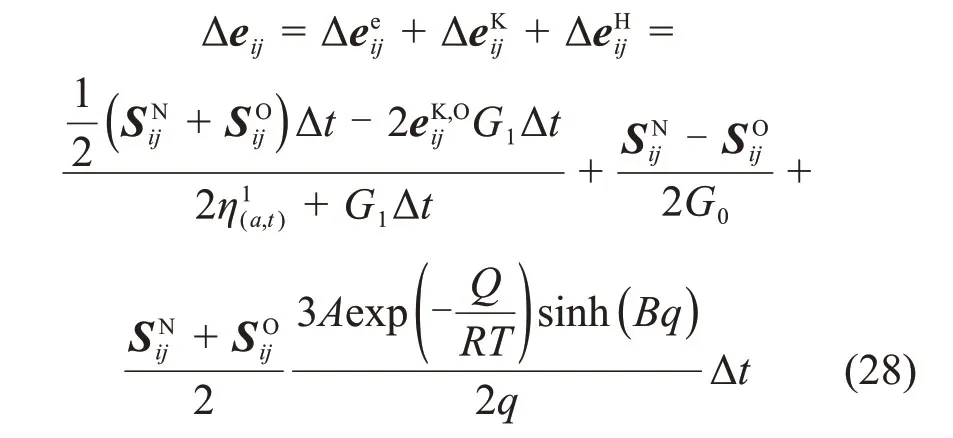
整理可得NGKH模型第i步应力更新公式为


3.2 二次开发程序的验证
基于C++语言,利用Visual Studio2010平台将上述NGKH蠕变模型本构方程的差分形式进行编译写入动态链接库.dll文件中,利用FLAC3D的UDM接口程序进行二次开发。图8所示为NGKH模型的二次开发流程。

图8 自定义NGKH本构模型二次开发流程Fig.8 Secondary development process of self-defined NGKH constitutive model
为了验证开发NGKH模型程序的正确性,建立与室内试验规格相同的直径为50mm、高度为100mm的盐岩圆柱体数值模型,共划分1 440个单元和1 595个节点,如图9所示。模型底面施加法向约束,顶面分别施加30,35,40和45MPa的均布载荷,侧面施加15MPa围压,分别进行三轴蠕变压缩试验。
3.2.1 黏弹性特征验证

图9 盐岩的有限差分数值试样Fig.9 Finite difference numerical sample for salt rock
由式(11)可知:当a=0时,非定常广义Kelvin模型退化为广义Kelvin模型,因此,在NGKH模型中将a和A同时设置为0,此时NGKH模型即退化为广义Kelvin模型。在FLAC3D程序内置的常规Burgers模型中,对Maxwell体串联牛顿黏壶的黏性系数不进行赋值,即退化为广义Kelvin模型。退化后的NGKH模型和退化后的Burgers模型均属于三元件模型,按照表4所示的广义Kelvin参数分别对这2个退化模型进行赋值,计算不同轴向载荷下的盐岩试样蠕变曲线。图10(a)~10(d)所示分别为偏应力25MPa时由退化NGKH模型计算得到的蠕变10,20,30和40 h后的盐岩数值试样位移分布云图,图11所示为不同偏应力下退化NGKH模型与退化Burgers模型的蠕变曲线对比图。
由图10可以看出:盐岩试样的顶部轴向位移最大,往底部方向逐渐减小;随着蠕变时间的增加,盐岩试样的最大轴向位移随之增大,但在20 h后轴向应变增速开始放缓。从图11可知:在非定常参数a及Heard体不起作用的情况下,退化NGKH模型与退化Burgers模型的瞬时应变一致,曲线吻合良好,表明开发的NGKH模型程序进行的黏弹性计算结果是可靠的。
3.2.2 非线性特征验证
按照表2中蠕变参数对NGKH蠕变模型赋值并进行三轴蠕变数值计算,图12所示为开发的NGKH模型程序模拟结果与室内试验结果的对比。其中图12(a)所示为不同偏应力下数值模拟结果与室内试验结果对比,图12(b)所示为不同温度下数值模拟结果与室内试验结果对比。从图12可以看出开发NGKH模型的程序模拟结果与室内试验结果吻合良好,证明该模型的非线性蠕变计算结果是可靠的。
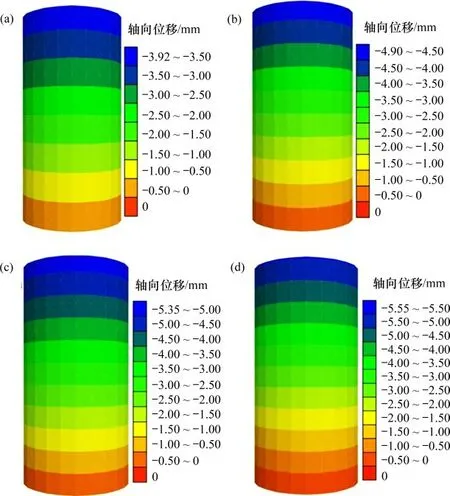
图10 不同蠕变时刻退化Burgers模型的轴向位移分布Fig.10 Axial deformation distributions of degenerated Burgers model at different creep time
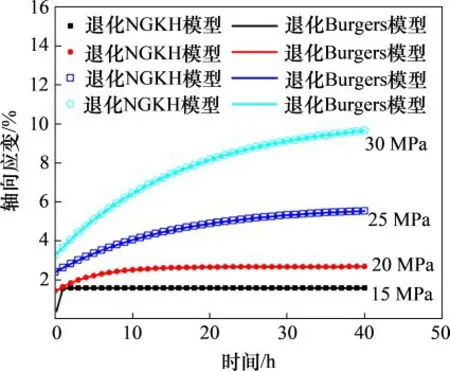
图11 退化NGKH模型和退化Burgers模型的黏弹性蠕变曲线对比Fig.11 Comparison of viscoelastic creep curves between degraded NGKH model and degraded Burgers model

图12 NGKH模型的非线性计算结果与试验结果的对比Fig.12 Comparison between nonlinear computation results from NGKH model and creep test results
上述分析验证了本文提出的将包含非定常黏壶的非定常广义Kelvin模型与稳态蠕变Heard体进行串联,最终构建NGKH蠕变模型以描述盐岩的非线性蠕变特征思路的正确性以及该蠕变模型在FLAC3D中二次开发的正确性。开发得到的FLAC3D蠕变本构模型为盐岩地层井壁围岩稳定性分析及套损问题研究提供了参考。
4 结论
1)将牛顿黏壶的黏滞系数视为时间的函数,采用非定常黏壶替换常规广义Kelvin模型中的线性牛顿黏壶,建立了非定常广义Kelvin模型,将其与非线性Heard体进行串联,组成能够描述盐岩瞬时蠕变阶段和稳态蠕变阶段的四元件非线性NGKH蠕变模型。
2)基于盐岩的室内三轴蠕变试验结果,对NGKH模型的蠕变参数进行辨识。拟合结果与室内试验曲线吻合良好,表明与广义Kelvin模型及非定常广义Kelvin模型相比,本文提出的NGKH蠕变模型更加适合描述川东北油气田嘉陵江组盐岩的非线性蠕变特征。
3)基于FLAC3D二次开发NGKH模型程序的黏弹性计算结果与非线性计算结果都是可靠的,从而证实了开发NGKH模型的正确性与合理性。

