差异变形下地铁盾构隧道内行车舒适性研究
施成华,刘建文,李翔,雷明锋,2,彭立敏
(1.中南大学土木工程学院,湖南长沙,410075;2.重载铁路工程结构教育部重点实验室,湖南长沙,410075)
随着城市化的不断发展,在既有地铁隧道邻近区域进行基坑开挖的现象频繁,国内外学者对此类问题进行了深入研究[1-3]。郑刚等[4]总结了近年来国内基坑施工引起盾构隧道变形的代表性工程案例,其中邻近基坑开挖引起盾构隧道最大隆起量可达33mm。基坑开挖引起的土体卸载会破坏下方既有地铁隧道的应力平衡,造成隧道线路局部隆起,不仅引起隧道结构管片开裂、螺栓屈服、接缝张开及渗漏水等病害,而且影响隧道内行车安全性及舒适性,因此,对隆起变形下隧道内列车运行动力性能进行研究尤为重要。国内外学者对列车行车安全性与平稳性开展了大量研究。CHENG等[5]基于线性蠕变模型,推导出曲线上铁道车辆运动的振动微分方程,采用线性和非线性模型分析了不同曲线半径的轨道条件下车速对安全性和平稳性的影响;张小会等[6]研究了行车速度及路基不均匀沉降对列车动力性能的影响。YAU[7]研究了在不均匀沉降的导轨梁上运行的磁悬列车动力响应问题,发现即使不均匀沉降很小,在车速较大的情况下,列车动力响应也会有明显放大的现象。RECUERO等[8]提出了一种能够有效地捕捉到中频车辆-轨道相互作用、接触片弹性和车辆动力学规律的方法。JU等[9]研究了一系列磁浮列车在多跨桥梁基础沉降和地震作用下的安全性问题。杨吉忠等[10-11]运用车辆-轨道耦合动力学模型对有砟轨道下沉变形特性、横风中的列车运行安全性进行了研究。CHELI等[12]分析了轨道不平顺对车体振动的影响,发现不同振动模态的激励对行车舒适性有很大影响。事实上,列车在地面路基上与地下隧道中行驶时,由于行车所处的环境不同,车辆振动与平稳性也有差别。当前,大量研究关注于地铁行车引起的隧道结构动力响应及周围环境的振动,具有代表性的有NEJATI等[13]的2D模型、GALVÍN等[14]的2.5D模型、FORREST等[15]的“Pipe-in-Pipe”模型、YANG等[16-17]的盾构隧道振动激励模型试验等,而关于地铁内行车安全性与平稳性的研究很少。当前大部分研究一般以铁路轨道不平顺谱作为外部激励,忽略了车辆、轨道、盾构隧道与围岩之间的相互作用,通常将邻近基坑开挖对既有盾构隧道的影响和列车行车安全性、舒适性分开单独进行研究,无法揭示地铁线路差异变形对列车行车产生的影响。为此,本文作者以1个基坑开挖引起既有下卧地铁线路隆起变形的工程案例为研究背景,建立车-轨-隧-围岩一体化模型,开展差异变形下地铁盾构隧道内行车舒适性研究,进而对行车舒适性影响因素进行分析并对列车行车舒适性限值进行讨论。
1 工程简介
1.1 工程概况
深圳市桂庙路快速化改造工程西起规划振海路,终于南海大道,道路全长约4.9 km。桂庙路改造工程需在既有地铁11号线上采用明挖法修建双洞矩形公路隧道,共线长度约3 km。其中,K3+840~K3+980段内基坑与地铁相对位置关系如图1所示。

图1 基坑与下卧盾构隧道相对位置关系Fig.1 Relative position between excavation and underlying shield tunnel
基坑开挖深度约20m,宽度约40m,围护结构为地下连续墙,墙厚1m,深度约30m。共线段地铁11号线盾构隧道左、右两线均位于基坑下方,隧道内径为6m,壁厚0.35m,与基坑底板净距约8 m。该标段内地层自上而下依次为素填土(厚2~3m)、砾质黏性土(厚7~10m)和粗砾花岗岩(厚20~25m)。为保证施工进度和土体稳定性,设计采用全幅、分层、分步开挖,施工步长为6m。
1.2 现场监测
基坑开挖时,除加强基坑监测外,开挖引起的隧道隆起变形会对运营列车的行车安全性和舒适性产生不利影响,因此,对下卧地铁11号线变形的监测尤为重要。将工程施工区域往两端各延伸20m作为开挖影响区域,在影响区域内,间隔2.5m布置监测断面,每个监测断面共布置4个监测点,分别位于道床,左、右拱腰和拱顶。
在工程建设过程中,K3+840~K3+980段地铁11号线发生明显隆起变形,实测左线隆起峰值已超过施工阶段控制值10mm,截至目前自动化监测隆起峰值基本稳定在14mm左右。
2 车-轨-隧-围岩一体化模型
随着计算机性能的提高和计算方法的发展,对于涉及基坑开挖引起下卧盾构隧道隆起变形的静力计算过程和隆起变形后地铁列车运营安全性、舒适性的动力计算,大多采用有限元法。为此,本文基于ABAQUS有限元平台,根据赫兹非线弹性接触理论模拟轮轨接触关系,考虑车辆、轨道、隧道、围岩的空间结构特征和相互接触关系,建立车-轨-隧-围岩一体化模型,具体包括地铁车辆模型、轮轨接触模型、轨道模型及隧道-围岩模型,以研究基坑开挖引起的隧道差异变形对地铁行车的影响。
2.1 地铁车辆模型
根据地铁车辆结构特点,车辆动力学模型包含车体、转向架以及轮对3种结构。车体与转向架之间通过二系悬挂弹簧连接,转向架与轮对之间通过一系悬挂弹簧连接。根据Hamilton原理建立车辆结构的动力学方程,该模型中车体、转向架和轮对采用实体单元模拟,用弹簧阻尼单元模拟一系、二系悬挂系统连接,地铁车辆模型如图2所示[18]。

图2 地铁车辆模型Fig.2 Metro vehicle model
2.2 轮轨接触模型
列车运行时,轮轨之间的相互关系可概化为图3所示的移动非线性Hertz弹簧模型。轮轨接触的法向力可采用如下公式计算[19]:

式中:P(t)为轮轨接触法向力;ΔZ(t)为接触点处轮轨间的法向弹性压缩量;G为轮轨接触常数。

图3 轮轨接触模型Fig.3 Wheel-rail interactionmodel
2.3 轨道模型
本案例地铁道床形式为短轨枕式整体道床,轨道振动主要体现在钢轨的振动上,钢轨与道床之间采用弹簧阻尼元件连接。仅考虑其垂向、横向及扭转自由度,图4所示为短枕式整体道床轨道动力模型纵断面图和横断面图。

图4 轨道动力学模型Fig.4 Dynamicmodelsof track
2.4 隧道-围岩模型
管片是盾构隧道最基本的单元,接头的存在是其最显著的特征。为准确模拟管片与管片、管片与围岩之间相互接触关系,基于三维非线性接触理论建立多尺度精细化三维盾构隧道-围岩模型,管环分为1个封顶块K(圆心角为21.5°)、2个邻接块B(圆心角为68°)和3个标准块A(圆心角为67.5°),管环宽度为1.5m,衬砌环接缝采用12个纵缝螺栓(M27)和16个环缝螺栓(M27)连接,错缝拼装。螺栓采用弯梁单元模拟,并将梁单元嵌入管片单元中,既可模拟接头的拉、压、剪切力学性质,也可模拟管片之间的相互作用。为提高计算效率,在基坑开挖影响范围外,隧道采用等效均质模型,刚度折减系数经验值取为0.78。管片与管片、管片与围岩之间的接触面法向行为均采用“硬接触”关系模拟。在接触面切向行为中,若接触面闭合,则接触面定义为可传递摩擦力。SHI等[1,20]介绍了该模型,并成功地应用于邻近基坑开挖对盾构隧道的影响研究和列车动载作用下管片结构静动力响应特性研究。
通过对本文工程案例进行分析,数值模型中隧道及线路的隆起变形主要通过隧道上部基坑开挖卸荷实现。模型主要针对K3+846~K3+946段,共计100m,基坑长30m,宽40m,深20m,与地铁隧道净距为8m。基坑开挖模型如图5所示。开挖分为6层10步进行(图5中间位置数据1~10表示开挖步序),在基坑施工过程中,考虑围护结构及支撑的作用。建立的车-轨道-隧道-土体三维动力学耦合模型局部放大图如图6所示。

图5 基坑开挖模型Fig.5 Excavationmodel

图6 车-轨-隧耦合动力学模型Fig.6 Dynamic train-track-tunnel-soil coupledmodel
3 模型参数与模型验证
3.1 模型参数
采用瑞利阻尼模型(Rayleigh damping),由质量阻尼系数α和刚度阻尼系数β确定模型中阻尼比系数。围岩与衬砌结构的相关力学参数见表1。地铁车辆为B型车,车辆及轨道模型参数见表2。
3.2 模型验证
为验证本文静、动力模型的有效性,基坑开挖引起下卧盾构隧道隆起变形(静力过程)采用案例验证,计算结果与现场实测结果对比见图7。列车荷载作用下隧道结构动力响应(动力过程)的验证可基于文献[21]中上海地铁9号线隧道振动实测值采用本文模型进行,隧道壁加速度频谱的计算值与实测值对比见图8。
由图7可知:基坑开挖所致隧道隆起变形的模型计算结果与现场实测结果基本吻合,且模拟计算的各测点隆起值随开挖步的变化也与实测结果一致。同时,图8表明采用本文中的车-轨-隧-围岩一体化模型计算得到的加速度谱与现场实测结果较吻合,验证了本文所采用的计算模型计算静、动力的有效性与准确性。

表1 围岩与衬砌相关力学参数Table1 Related mechanical parameters of soil and lining

表2 车辆与轨道相关力学参数Table2 Related mechanical parameters of vehicle and track

图7 隧道隆起变形曲线对比Fig.7 Comparison between simulations and measurements of tunnel heave
4 列车动力性能分析
4.1 行车安全性分析
在车-轨耦合系统分析中,常选取脱轨系数和轮重减载率作为评估列车运行安全性的主要指标。轮重减载率一般用于轮对横向力等于零的情况,适用于本文研究对象。
分别提取隧道隆起变形为15mm、行车速度为72 km/h时首节车厢第1和第2轮对处车轮与轨道之间的竖向接触力,计算并绘制轮重减载率时程曲线,如图9所示。

图8 隧道壁加速度频谱对比Fig.8 Comparison between simulation values and measurement values of acceleration spectrum on tunnel side wall

图9 轮重减载率时程曲线Fig.9 Time-history of wheel load reduction ratio
由图9可知:各轮对轮重减载率时程曲线均呈现“增—减—增—减”趋势,每条时程曲线中第1个波峰出现在列车刚驶入隆起段线路,车轨接触不稳定,减载率较大;第1个波谷出现在列车稳定行驶在隆起线路段,该时段列车行驶平稳,轮重减载率较低;第2个波峰也是该时程曲线的峰值,出现在轮对刚刚驶过线路的隆起顶点即t=0.63 s和0.74 s时,此时,列车车轮由“上坡”变为“下坡”,出现类似于“跳车”的现象是最危险的时段。
以上2轮对轮重减载率最大值分别为0.020 9和0.023 96,与规范[22]规定的标准值0.600 00相差甚远。可见:当列车以正常运行速度行驶在隆起程度不超过规范控制值且无明显横向荷载的盾构隧道段时,地铁列车不易出现脱轨事故,行车安全性较高。
5.2 行车舒适性分析
国内常用列车车体振动加速度及平稳性指标2个标准来评判列车行车舒适性[22],本文选取后者进行分析研究。我国列车运行平稳性指标W采用Sperling指标:

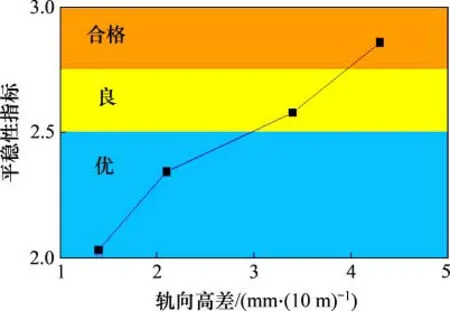
式中:A为列车车体振动加速度;f为列车振动频率;F(f)为频率修正系数。规范[22]规定:当地铁列车运行平稳性指标W≤2.50时,行车舒适性评级为“优”;当2.50 由图10可知:列车行驶在线路隆起段时,垂向加速度时程曲线除自身震荡外,总体上呈现一定的波动性,前车厢垂向加速度峰值为0.058m/s2,后车厢垂向加速度峰值为0.053m/s2。车厢垂向振动加速度时程曲线变化趋势为:列车行驶在隆起前半段即“爬坡”段,对应时间分别为前车厢0.5~1.0 s,后车厢1.5~2.0 s,垂向加速度均值出现正向峰值;达到隆起段顶点时(前车t=1.0 s,后车t=2.0 s),垂向加速度均值降到0m/s2左右;在行车“下坡”段(前车1~2 s、后车2~3 s),车辆垂向加速度均值呈现负值,之后稳定在0m/s2左右震荡。 图10 车厢垂向振动加速度-时程曲线Fig.10 Vertical acceleration-time curves of vehicle 计算前后车行车平稳性指标分别为2.577 1与2.549 5,可见地铁列车运行在该线路隆起段时,前后两车厢平稳性指标均不达标,仅处于“良”等级,不满足规范中“优”的要求,且前车行车舒适性比后车略差。 经过以上分析可知:不考虑其他荷载因素,当地铁列车行驶在基坑开挖引起的隧道线路隆起段时,列车在正常运行速率下行驶不会出现安全问题,但地铁列车大多为客车,所以,需要满足乘客乘坐的舒适性即列车运行舒适性要求。这里对隆起变形下盾构隧道内行车舒适性影响因素进行研究,着重考虑隧道隆起程度和列车行车速度2个主要因素。 隧道隆起程度主要通过轨向高差体现。选取隧道隆起变形峰值为5,10,15和20mm时对应的轨向高差1.4,2.1,3.4和4.3mm/(10m)作为隧道隆起变形量,提取隧道不同隆起变形工况下前车垂向加速度时程曲线,如图11所示。 由图11可知:在各工况下,车体垂向振动加速度峰值分别为0.023,0.045,0.058和0.065m/s2,可见线路钢轨轨向高差在一定程度上影响列车运行振动加速度;隆起值越大,车体垂向加速度越大。对以上4条曲线进行快速傅里叶变换,求解其平稳性指标,如图12所示。 从图12可见:列车平稳性指标与线路轨向高差值基本上呈线性关系;当轨向高差达到3.4mm/(10m)时,行车平稳性指标已经超过规范规定值2.500 0;当轨向高差达4.3mm/(10m)时,行车平稳性指标达到2.856 7,按照规范评级为“合格”,不满足规范规定的“优”的标准,极有可能出现乘客乘坐不舒适问题。 分别提取36,54,72,90和108 km/h共5种车辆运行速率下后车车体的垂向振动时域曲线,并进行平稳性指标求解,结果如图13所示。 由图13可知:平稳性指标相对于行车速率增大呈现指数增大趋势;当行车速率低于54 km/h时,列车运行平稳性指标处于规范值2.500 0以内,乘客乘行车舒适性较好;当车速达到72~90 km/h时,平稳性指标处于2.500 0~2.750 0之间,行车舒适性评级为“良”;当车速增大到108 km/h后,平稳性指标迅速增大,达到2.973 4,处于合格线边缘,此时列车运行舒适性较差,无法满足乘客乘坐的舒适性要求。 图11 不同隆起工况下车体垂向加速度-时程曲线Fig.11 Vertical acceleration-time curves of vehicle in different tunnelheave cases 图12 盾构隧道隆起值与平稳性指标关系Fig.12 Relationship between tunnel heave and stability index 图13 列车运行速率与平稳性指标的关系Fig.13 Relationship between train running speed and stability index 由以上分析可知,当地铁列车行驶在隧道隆起段时,行车平稳性指标与隧道隆起程度及列车行车速度均呈正相关关系,针对上述2个因素共20个工况下的平稳性指标数据进行二元回归分析,得到列车运行平稳性指标W与隧道隆起程度、行车速度的关系: 式中:v为列车运行速率,km/h;Δh为盾构隧道轨向高差最大值,mm/(10m)。由式(3)计算得到平稳性指标为2.50,2.75和3.00时的Δh-v曲线,见图14。 由图14可知:当隧道轨向高差峰值达到规范规定预警值2mm/(10m)时,平稳行车速度约为80 km/h;当隧道轨向高差峰值达到规范控制值4mm/(10m)时,平稳行车速度仅为20 km/h左右,若超过此速度行驶,则会产生舒适性问题,乘客行车舒适性降低;当地铁列车平稳行车时,其车速与隧道轨向高差峰值呈现负相关关系,隧道轨向高差峰值越大,平稳行车车速越低;当盾构隧道轨向高差峰值超过3.5mm/(10m)时,列车平稳运行车速下降明显,此时,为了达到平稳行车要求,需对车速进行控制。 图14 平稳行车车速与线路轨向高差的关系Fig.14 Relationship between train velocity and rail altitude difference 1)基于赫兹非线弹性接触理论,考虑车辆、轨道、隧道、围岩的空间结构特征和相互作用关系,构建了车-轨-隧一体化计算模型,建立了差异变形影响下盾构区间隧道内行车舒适性的计算方法。 2)采用建立的计算模型,分析了隆起变形下盾构隧道内运行车辆的安全性和舒适性。当盾构隧道隆起变形不超过规范控制值且地铁列车以正常运行速度行驶时,能够保证隧道内的行车安全,但会对隧道内列车运行的舒适性产生一定影响。 3)地铁列车以正常运行速度行驶在线路隆起段时,由车体垂向振动加速度计算得出的平稳性指标与线路轨向高差呈现线性关系,与行车速度呈指数关系;当隧道轨向高差达到规范规定预警值2mm/(10m)时,平稳行车速度约为80 km/h;当达到控制值4mm/(10m)时,满足行车舒适性要求的车速仅为20 km/h左右。
5 行车舒适性影响因素分析
5.1 隧道隆起程度
5.2 行车速度


5.3 列车行车舒适性限值讨论


6 结论

