正交各向异性功能梯度微板的自由振动行为
(中国石油大学(华东)储运与建筑工程学院,山东青岛,266580)
功能梯度材料是材料组分或几何尺寸沿结构特定方向成连续梯度变化的一种新型功能材料,它具有消除应力集中、减小残余应力、增强连接强度、减小裂纹驱动力等许多普通均质材料不具备的优异性能[1-3]。随着微电子科技的发展,功能梯度微结构的应用更加广泛,众多的微观实验发现并证实,当金属或复合材料构件的特征尺寸减小到一定范围时,其力学性能随着特征尺寸的改变而变化,表现出较强的尺度效应[4-5]。为对该现象作出合理解释且方便建模,许多学者在弹性体的本构关系中引入与微观结构相关的特征尺度参数,提出偶应力理论用以描述材料力学行为的尺度依赖性。YANG等[6]在偶应力理论基础上,提出了修正偶应力理论,该理论只引入1个长度尺度参数,简化了建模过程,更便于实际应用。ASGHARI等[7]基于修正偶应力理论在线弹性范围建立了能够描述功能梯度Timoshenko微梁弯曲及自由振动尺度效应的力学模型。KE等[8]基于修正偶应力理论分析了功能梯度Timoshenko微梁的动态稳定性问题。在修正偶应力理论的基础上,REDDY[9]利用Euler-Bernoulli和Timoshenko梁理论,研究了功能梯度微梁的弯曲,自由振动和屈曲行为。DEHROUYEH-SEMNANI等[10]基于修正偶应力理论,通过参数分析研究了微尺度梁剪切变形的尺度效应,并对微尺度梁的静弯曲、屈曲和自由振动等力学问题进行了研究。DAI等[11]基于修正偶应力理论,考虑大变形和尺度效应,提出一种非线性模型描述悬臂微梁的共振特性。除此之外,许多专家学者对微板的力学行为的尺度效应进行了理论研究。TSIATAS[12]基于修正偶应力理论和Kirchhoff板理论,建立了能够描述不同边界条件下任意边界形状微板静弯曲行为尺度效应的力学模型。KE等[13-14]基于修正偶应力理论,研究了不同边界条件下Kirchhoff和Mindlin微板自由振动行为。THAI等[15]基于3种不同板理论对功能梯度微板的弯曲,自由振动以及屈曲行为进行分析并探讨了材料尺度参数对板弯曲挠度,自振频率以及屈曲载荷的影响。LOU等[16]考虑几何非线性,基于修正偶应力理论提出一种能够描述功能梯度微板尺度效应的统一高阶板理论,并利用哈密顿原理推导了微板的控制方程和边界条件。随着材料科学的发展和实际工程需要,各向异性的功能梯度微结构的应用愈发广泛,针对其力学行为研究也得到青睐。CHEN等[17]将偶应力理论推广到各向异性材料,提出了一种新修正偶应力理论,并基于该理论开展了一系列有关层合梁板结构弯曲、振动和稳定等问题的研究[18-19]。贺丹等[20-21]]基于新修正偶应力理论,对平面正交各向异性功能梯度微梁和斜交铺设层合Kirchhoff微板的弯曲行为的尺度效应进行研究。YANG等[22]基于新修正偶应力理论和虚功原理研究了正交各向异性功能梯度Kirchhoff微板在弯曲变形过程中挠度和正应力的尺度效应。上述研究均假设材料参数以幂指数形式变化,定性分析了各向异性和指数变化对微结构挠度、应力和固有频率尺度效应的影响。本文作者基于新修正偶应力理论和Kirchhoff板理论,定量研究材料参数沿板厚方向呈正弦梯度变化的正交各向异性简支微板的弯曲和自由振动行为,重点考察各向异性和功能梯度参数对微板挠度、偶应力和固有频率尺度效应的影响。本研究可为微电子机械系统(MEMS)中微结构的优化设计和力学分析提供理论基础和技术参考。
1 新修正偶应力理论
CHEN等[17-19]提出新修正偶应力理论,并给出了弹性体应变分量εij和曲率分量χij的表达式为:

式中:ui为平动位移分量;

ωi为转动位移分量;eijk为置换符号。
各向异性弹性体的本构关系可以描述为:

式中:Cijkl为弹性常数分量;σij为应力分量;mij为偶应力分量;Gi和Gj分别为2个正交方向的剪切模量;li和lj分别为2个正交方向的材料尺度参数。
2 微板动力学模型建立
2.1 基本变量描述
图1所示为正交各向异性微板示意图,其中:a,b和h分别为微板的长度、宽度和厚度;xy平面与微板的中面重合。根据Kirchhoff板假设,板的位移场为

式中:u,v和w分别为板内任意一点沿x,y和z方向上的位移分量;u0和v0分别为变形后板中面沿x和y方向上的位移;t为时间。将位移分量表达式(6)代入几何方程式(1),得到微板的非零应变分量为

将位移分量表达式(6)和转动位移表达式(3)代入曲率分量表达式(2),得到微板的非零曲率分量:

由式(4)可知本构关系可以表示为


图1 正交各向异性微板示意图Fig.1 Schematic diagram of orthotropicmicroplate
式中:

和

分别为应力列向量和应变列向量。刚度矩阵K中非零元素为

式中:μxy和μyx分别为材料不同方向的泊松比;Ex和Ey分别为材料沿x和y方向的弹性模量;Gxy,Gxz和Gyz为材料不同方向的剪切模量;lx和ly分别为材料沿x和y方向的特征尺度参数。
2.2 动力学微分方程
哈密顿原理亦称最小作用原理,表述为:受完整约束的有势系,在位形空间中,相同时间通过两位形点间的一切可能运动曲线中,真实运动曲线使作用量取极小值,即作用量的一阶变分为零,表示为

式中:在时间间隔[t1,t2]内微板虚动能为

式中:ρ为密度;u为板的平动位移;V为体积;Ω为中性面面积;∂Ω为其边界;系数h1,h2,h3和h4分别为

式中:nx和ny分别为中面边界外法线与x和y轴的夹角余弦,

在时间间隔[t1,t2]内微板虚应变能为

式中:

面内合力与合力矩以及合偶应力表达式为

令

式中:n和s分别为板边界的法向和切向。将式(18)代入式(16)得

式中:q7=nxp6+nyp7;q8=-nyp6+nxp7。对于矩形板,边界为直线,所以,∂w∂n=∂w∂s,对式(19)进行分部积分可得


式中:[q8]i为q8在i个转角处的跳跃值。
在时间间隔[t1,t2]内外力虚功为

式中:ωx和ωy为转动位移分量;fT为体力;-fT为表面力。
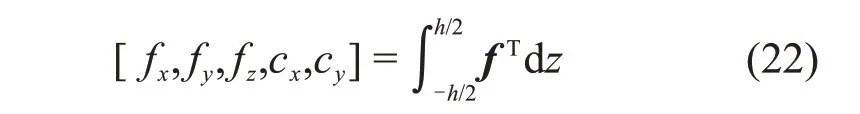

将式(23)代入式(21)并进行分部积分,化简得

将式(13),(20)和(24)代入式(12),得

式中:S1=h1-p1+fx;S2=h2-p2+fy;S3=h3-为转角;wi为挠度在第i个转角处的跳跃值。对任意的δu0,δv0和δw,式(25)均成立,可得运动控制方程:

和相应的边界条件为

将式(6)~(9)代入式(26),得到位移表示的微分控制方程:

式中:

对于微板在横向分布载荷q(x,y)作用下的静态弯曲行为,忽略式(28)中位移的时间导数项,可得微板静力学平衡方程为

3 微板动力学模型求解
以四边简支微板为例,如图2所示,对正交各向异性功能梯度微板弯曲挠度和自由振动频率的尺度效应进行研究。其材料参数Ex,Ey,Gxy,Gxz,Gyz,ρ,lx和ly均沿板厚方向呈正弦梯度变化,梯度函数为

式中:上标s表示微板上下表面;上标c表示微板中面,

α为定义的量纲一的功能梯度参数,当α=1时,材料模型退化为正交各向异性均质模型。
简支板的边界条件为


图2 正交各向异性功能梯度简支微板示意图Fig.2 Schematic diagram of orthotropic functionally graded simply supportedmicroplate
3.1 微板位移求解
工程中任何形式的载荷均可描述为三角级数的形式,为了描述微板结构所承受实际载荷的复杂情况,设作用于微板的载荷函数关系式为

设满足式(33)的位移势函数为


式中:

将位移表达式(35)代入几何方程(7)和本构方程(9),可得微板偶应力表达式为

为了便于分析,定义量纲一的坐标,量纲一挠度和量纲一偶应力的表达式为

3.2 微板固有频率求解
基于Navier法,将满足微板边界条件式(33)的位移函数描述为双三角级数解的形式:
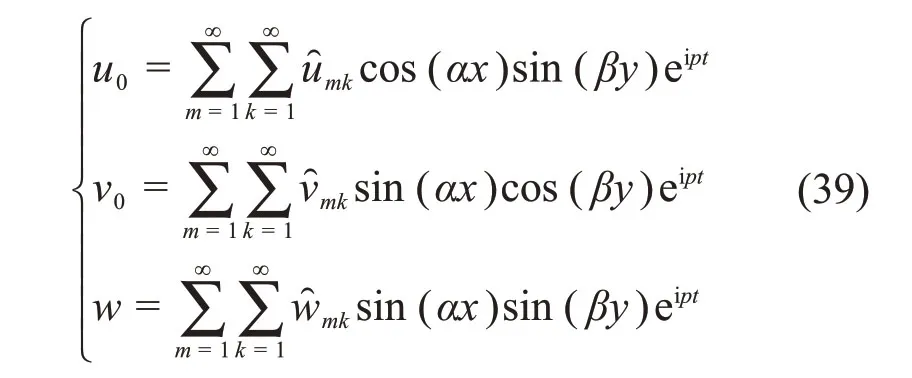
式中:p为板的固有频率;i为虚数单位,i2=-1。为待定系数。将式(39)代入位移表示的运动控制方程式(28)得

式中:D为刚度矩阵,矩阵中各元素表示为
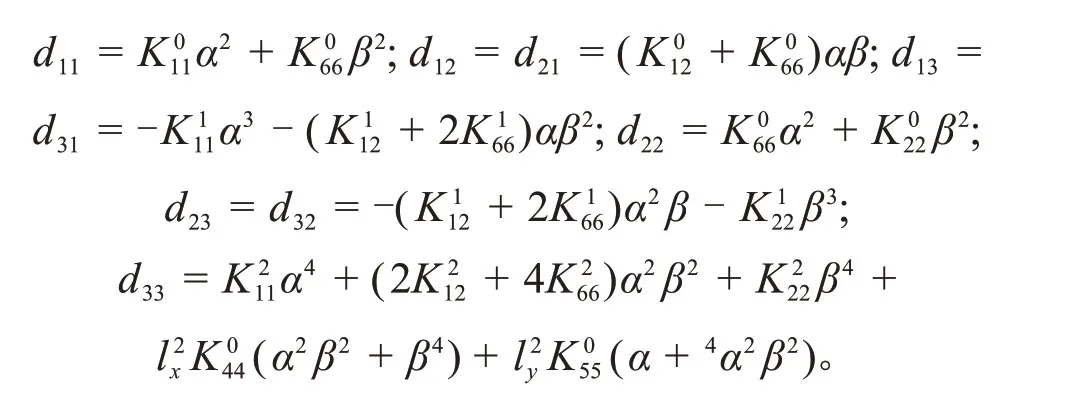
M为板的质量矩阵,矩阵中各元素表示为

由于待定系数的取值具有任意性,故求固有频率p可以转化为求刚度矩阵对质量矩阵的广义特征值。为了便于分析,将微板量纲一固有频率的表达式定义为

4 数值结果与讨论
据上述力学模型,对正交各向异性功能梯度简支微板前三阶固有频率以及其在双向正弦载荷作用下的挠度和偶应力进行数值计算。其材料参数如表1所示,载荷参数q0=1 000MPa,微板的结构尺寸为h=0.025mm,a/h=10,a=b。

表1 正交各向异性功能梯度微板材料参数[23]Table1 Materialparametersof orthotropic functionally gradientmicroplate[23]
4.1 挠度分析
图3所示为h/lx取值不同时,微板在y=b/2处截面的量纲一的挠度沿x方向的分布曲线。从图3可以看出:微板沿x方向的挠曲线均呈正弦分布,且最大挠度出现在微板中间位置。

图3 不同h/lx下微板沿x方向的量纲一的挠度w′分布Fig.3 Dimensionlessdeflection ofmicroplatewith different h/lx
图4(a)所示为不同功能梯度参数下,微板中心量纲一的挠度随h/lx的变化曲线。从图4(a)可以看出:当h/lx小于5时,微板量纲一的挠度较小,微板挠度具有明显的尺度效应;随着h/lx增大,微板量纲一的挠度逐渐增大,但增大程度逐渐减缓,表明h/lx对微板沿x方向挠曲线的影响逐渐减弱;当h/lx大于10时,微板最大量纲一的挠度基本保持恒定,微板挠度的尺度效应消失。

图4 不同功能梯度参数下微板最大量纲一的挠度w′变化曲线Fig.4 Maximum dimensionless deflection ofmicroplate with different functionally graded parameters
图4(b)所示为不同功能梯度参数下,微板中心最大量纲一的挠度随h/ly的变化曲线。从图4(b)可以看出:当功能梯度参数较小时,微板最大量纲一的挠度较小;随着功能梯度参数增大,微板最大量纲一的挠度逐渐增大,但增大程度逐渐减缓,表明功能梯度参数对微板挠度的影响逐渐减弱。除此之外,通过对图4(a)和4(b)进行对比可以发现,h/ly也是影响微板挠度尺度效应的重要因素,但沿2个正交方向的材料尺度参数对微板挠度的尺度效应影响程度不同。
4.2 偶应力分析
图5所示为h/lx取值不同时,微板量纲一的偶应力mx'在x=a/2处截面沿y方向的变化曲线。从图5可以看出:微板量纲一的偶应力mx'均沿y方向呈余弦分布,且最大偶应力出现在微板边界位置,中心处偶应力为零。

图5 不同h/lx下微板量纲一的偶应力mx'分布曲线Fig.5 Dimensionless couple stressofmicroplatewith different h/lx
图6所示为h/ly取值不同时,微板最大量纲一的偶应力mx'随h/lx变化曲线。从图6可以看出:当h/lx小于5时,微板量纲一的偶应力较大,微板最大量纲一的偶应力mx'随板厚与材料尺度参数比变化明显,具有明显的尺度效应。随着h/lx增大,量纲一的偶应力逐渐减小,但减小程度逐渐减缓,表明h/lx对微板偶应力的影响逐渐减弱;当h/lx大于12时,微板偶应力趋于0,尺度效应消失。
图7所示为不同功能梯度参数情况下,微板最大量纲一的偶应力mx'随h/lx的变化曲线。从图7可以看出:当功能梯度参数较小时,微板最大量纲一的偶应力mx'较大,随着功能梯度参数增大,微板偶应力逐渐减小,但减小程度逐渐减缓,表明功能梯度参数对微板偶应力的影响逐渐减弱。
4.3 固有频率分析
图8(a)所示为h/ly取值不同时,微板一阶量纲一的固有频率随h/lx变化曲线。从图8(a)可以看出:微板一阶量纲一的固有频率随h/lx的增大而减小;当h/lx小于5时,微板一阶量纲一的固有频率随h/lx变化明显;当h/lx大于10时,微板一阶量纲一的固有频率趋于稳定值,其尺度效应消失。

图6 不同h/ly下微板最大量纲一的偶应力mx'随h/lx的变化曲线Fig.6 Maximum dimensionless couple stressof microplate vs.h/lx for differentdimensionless thickness h/ly

图7 不同功能梯度参数下微板最大量纲一的偶应力mx'随h/lx的变化曲线Fig.7 Maximum dimensionless couple stressof microplate vs.h/lx with different functionally graded parameters
图8(b)所示为h/lx取值不同时,微板一阶量纲一的固有频率随h/ly变化曲线。从图8(b)可以看出:微板一阶量纲一的固有频率随h/ly的增大而减小;当h/ly小于3时,微板一阶量纲一的固有频率随h/ly变化明显;当h/ly大于6时,微板一阶固有频率趋于稳定值,其尺度效应消失。除此之外,通过对图8(a)和8(b)进行对比可以印证,沿2个正交方向的材料尺度参数对微板一阶固有频率的影响不同。

图8 微板一阶量纲一的固有频率p′11的变化曲线Fig.8 Curvesof dimensionless firstordernatural frequency of microplate
图9所示为h/ly取值不同时,微板二阶量纲一的固有频率随h/lx变化曲线。从图9可以看出:微板二阶量纲一的固有频率随h/lx的增大而减小;当h/lx小于5时,微板二阶量纲一的固有频率随板厚与材料尺度参数比变化明显;当h/lx大于10时,微板二阶固有频率趋于稳定值,其尺度效应消失。
图10所示为h/ly不同时,微板三阶量纲一的固有频率随h/lx变化曲线。从图10可以看出:微板三阶量纲一的固有频率随h/lx的增大而减小,当h/lx小于5时,微板三阶量纲一的固有频率随板厚与材料尺度参数比变化明显;当h/lx大于10时,微板三阶固有频率趋于稳定值,其尺度效应消失。

图9 微板二阶量纲一的固有频率p′21随h/lx的变化曲线Fig.9 Dimensionless second ordernatural frequency of microplate vs.h/lx

图10 微板三阶量纲一的固有频率p′31随h/lx的变化曲线Fig.10 Dimensionless third ordernatural frequency of microplate vs h/lx
图11所示为不同功能梯度参数下,微板一阶量纲一的固有频率随h/lx的变化曲线。从图11可以看出:当功能梯度参数较小时,微板一阶量纲一的固有频率较大;随着功能梯度参数增大,微板一阶量纲一的固有频率逐渐减小并逐渐趋于稳定值,表明功能梯度参数对微板固有频率的影响逐渐减弱。

图11 不同功能梯度参数下微板一阶量纲一的固有频率p′11随h/lx变化曲线Fig.11 Dimensionless firstordernatural frequency of microplate vs.dimensionless thickness h/lx with different functionally graded parameters
5 结论
1)板厚与材料尺度参数比越小,微板挠度、偶应力和前三阶固有频率的尺度效应越明显;当板厚与材料尺度参数比大于10,微板挠度、偶应力和前三阶固有频率的尺度效应可以忽略不计。
2)沿2个正交方向的材料尺度参数对微板挠度、偶应力和固有频率的尺度效应影响程度不同。
3)功能梯度参数对微板挠度、偶应力和前三阶固有频率的尺度效应有一定影响,且随着功能梯度参数增大,功能梯度参数对微板挠度、偶应力和固有频率的影响逐渐减弱。

