一类具有产毒浮游植物的交叉扩散浮游生物模型的图灵斑图
刘婷婷,彭亚红
(东华大学 理学院,上海 201620)
我国经济的日益发展以及人口日渐增多,导致环境遭受的污染越来越严重。人们缺乏环境保护的意识,导致水资源恶化严重,因此浮游生物大量繁衍暴发的现象频繁出现。在2007年,中国第三大淡水湖——太湖由于藻类植物的暴发,直接导致水源被严重污染,给当地生态环境和淡水养殖业产生了不容小觑的影响。对于此类浮游生物暴发现象,有关学者通过建模,试图先从理论上对这一问题进行研究[1-4],进而为解决实际问题提供指导。
早在2000—2001年,Chattopadhayay等[5]对浮游植物暴发现象进行实地考察并采集一定数据对此进行分析,根据分析统计的结果,建立了浮游植物释放毒素的浮游生物模型,如式(1)所示。
(1)
其中:P=P(t)和Z=Z(t)分别为浮游植物种群和浮游动物种群在t时刻的浓度;r和K分别为浮游植物种群的内秉增长率和环境容纳量;c为生物量之间的转化系数;μ为浮游动物种群的自然死亡率;f(P)为浮游植物被浮游动物捕食的函数;g(P)为浮游植物种群释放有毒物质的函数。
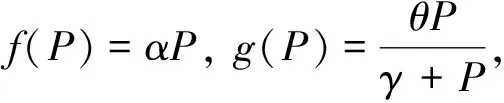
(2)
式中:β=cα;θ为浮游植物种群的毒素释放率;η为密度制约系数。文献[1]在模型(2)中引入自扩散系数,并在Neumann边界条件下考虑如下的扩散模型:
(3)
式中:P=P(x,t),Z=Z(x,t),Ω为具有光滑边界∂Ω的有界区域;v为∂Ω的外法单位向量;d1和d2分别为浮游植物和浮游动物的自扩散系数;ΔP和ΔZ分别为P和Z的拉普拉斯算子。假设上述模型中的所有参数均为正常数。
对空间扩散模型(3),文献[1]先证明了正平衡点是局部渐进稳定的,接着通过构造Lyapunov函数,进一步证明了正平衡点是全局渐近稳定的。
同时,许多学者研究了具有交叉扩散的反应扩散模型的动力学行为[6-11]。而文献[12-14]的研究表明,交叉扩散项的出现会对模型动力学行为产生影响。本文在文献[1]的研究基础上,在模型(3)中引入交叉扩散项,考虑如下模型:
(4)
其中:d11>0,d22>0分别为浮游植物和浮游动物种群的自扩散系数;d12∈R,d21∈R分别为浮游植物和浮游动物种群的交叉扩散系数。涉及的其他参数均为正常数,并假设式(5)成立。
d11d22-d12d21>0
(5)
1 模型(4)正平衡点的稳定性分析
易知,当且仅当
P* (6) 时,模型(4)存在唯一的正平衡点E*(P*,Z*),其中: 定理1不等式(6)成立当且仅当 (7) 证明由于P*是方程 的正根,显然有式(8)成立。 (8) 又因为P* (9) 成立。 不等式(9)成立当且仅当 (10) 和 (11) 同时成立。 不等式(10)成立当且仅当不等式(8)成立。不等式(11)成立当且仅当 (12) 成立,即式(9)成立当且仅当式(12)成立。从而定理1得证。 引理1(文献[1]中定理3.2和3.3) (1) 如果模型(3)满足条件(7),则模型(3)存在唯一的正平衡点E*(P*,Z*),且正平衡点E*是局部渐近稳定的; 由引理1可知,在浮游植物产生有毒物质的浮游生物模型中引入自扩散项之后,该模型的正平衡点仍旧是稳定的,即自扩散项的引入并未引起系统正平衡点稳定性的变化。 令 则模型(2)在E*处的雅可比矩阵为 显然,a11<0,a12<0,a22<0。由于 所以a21>0。从而有 T0=a11+a22= D0=a11a22-a12a21= 模型(4)在E*处的稳定性由如下特征方程的特征值决定。 λ2-Tkλ+Dk=0,k=0,1,2,… 其中: Tk=[T0-k2(d11+d22)] Dk=D0-k2(a11d22+a22d11-a21d12-a12d21)+ 这里 由Tk的表达式知,对∀k≥0,显然有Tk<0。根据式(5)和D0>0可知,Dk是关于k2的开口向上且截距为正的一元二次多项式,所以可能存在k∈N+,使得Dk<0。这是由于交叉扩散项d12或d21的出现引起的。考虑Dk的对称轴表达式为 注意到在临界值 时,Dk取到如下最小值: 模型(3)中,自扩散项的加入未引起正平衡点稳定性的变化,接下来讨论模型(4)引入交叉扩散项后正平衡点稳定性的情况。根据上文分析可知,产生图灵不稳的必要条件为 (13) (14) 式(13)成立当且仅当 (15) 式(14)成立当且仅当 (16) 若式(16)成立,显然式(15)成立。 定理2假设参数d12,d21∈R,模型(4)中其他参数均为正常数并满足条件(5)和(7),如果式(16)成立,则模型(4)的正平衡点E*(P*,Z*)是不稳定的。 L1为0.08-d12d21=0 由图1可知,曲线L1和图灵分支曲线L2所交区域D1和D2为图灵不稳区域。其中,D1分布在三、四象限,D2分布在一、四象限,且D1和D2表示如下: D1={(d21,d12)|d12<0,0.08-d12d21>0且 0.172 3d12+0.405 938<0} D2={(d21,d12)|d21>0,0.08-d12d21>0 0.172 3d12+0.405 938<0} 1.1节给出了模型(4)在正平衡点处不稳定的必要条件。模型(4)引入交叉扩散之后,交叉扩散的出现可能会引起系统不稳定的发生,由于模型(4)是在Neumann边界条件下讨论,而波数k是离散的,依赖于Neumann边界条件,因此,需进一步分析模型(4)的图灵不稳定的充分条件。为方便起见,在模型(4)中取空间变量为一维,即令Ω=(0,l)。下面分析引起模型(4)正平衡点不稳定的充分条件[12]。 记: (17) 由于d12,d21∈R,根据式(17)可知,存在d12或d21使M<0。 (18) (19) 也即 (20) 成立,其中M由式(17)给出。 由以上分析可得模型(4)的正平衡点不稳定的充分条件,即定理3。 定理3假设d12,d21∈R,模型(4)的其他参数均为正常数并满足条件(5)和(7)以及式(15)和(16),若存在正整数n,使得式(20)成立,则模型(4)的正平衡点E*(P*,Z*)是不稳定的。 为了验证定理3中满足条件的正整数n存在,下面举例说明。 根据曲线l1和曲线l2表达式可知,当取d21=2时,n1=0.223 6,n2=1.277 9,则取到一个n=1满足式(19)。 通过以上理论分析,得知模型(4)在引入交叉扩散项之后出现图灵不稳。在d21-d12平面上,得到不稳定区域D1和D2。本节对不稳定区域及其他区域进行数值模拟。由于浮游植物种群和浮游动物种群模拟出的斑图类型是类似的,所以在下文的数值模拟中,仅对浮游植物种群进行模拟。 在上文分析中已经得知模型(4)的图灵不稳定是由交叉扩散系数d12或d21引起的,在接下来的数值模拟中,固定r=1.5,K=17,α=0.063,β=0.038 7,μ=0.035,η=0.09,θ=0.1,γ=1.5,d11=0.4,d22=0.2。d12和d21取不同数值,在图1中取点验证。 (1) 固定d12=-7.5,取d21=2.35,0.029进行数值模拟,结果分别如图2和图3所示。 在图1中取(d21,d12)=(2.35,-7.5),该点在d21-d12平面的第四象限中,且在稳定区域中。由图2可知,随着时间变化,模型很快出现稳定状态。 在图1中取(d21,d12)=(0.029,-7.5),该点在不稳定区域D1中。由图3可知,随着时间变化,底部变为黄色区域,在黄色区域中出现大量的蓝色点状斑图,再经过一段时间的变化,最终稳定下来形成点条型斑图。 (2) 固定d21=2.499,取d12=-0.46和1.222进行数值模拟,结果分别如图4和5所示。 在图1中取(d21,d12)=(2.499,-0.46),该点在不稳定区域D2中。由图4可知:起初出现无规律的紫色块状,随着时间的延长,开始隐约出现条状和点状的斑点;随着时间再进一步延长,点状和条状逐渐明显,并且点状斑图连接成条状,最终,基本上以条状斑图稳定下来。 在图1中取(d21,d12)=(2.499,1.222),此点在不稳定区域D2上方的区域中。由图5可知,随着时间延长先出现一些不规则的红色斑点,但模型很快出现稳定状态。 本文主要讨论了交叉扩散对具有产毒浮游植物的浮游生物系统稳定性的影响,与仅含有自扩散项的浮游生物模型对比,交叉扩散项d12或d21的出现引起图灵不稳。在数值模拟部分,分别固定交叉扩散系数d12(改变d21的取值)和d21(改变d12的取值),发现交叉扩散系数d12或d21中任一个量的改变都会引起图灵不稳定性发生,从而产生丰富的图灵斑图,如点条混合斑图或条状斑图。同时,稳定性区域的模拟结果与理论结果也是一致的。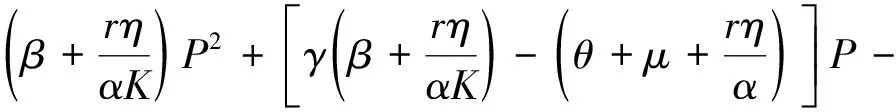
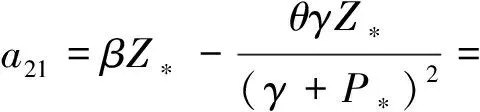
k4(d11d22-d12d21)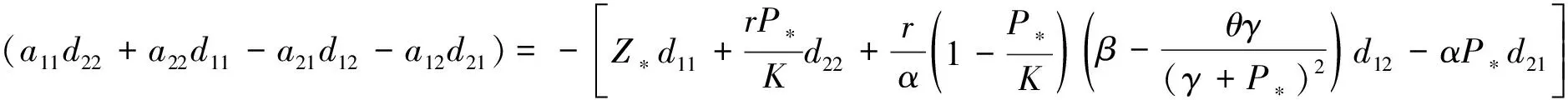
1.1 图灵不稳定的必要条件

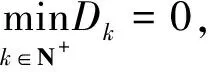
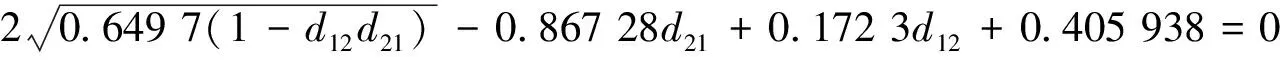
1.2 在有界区间中图灵不稳定的充分条件
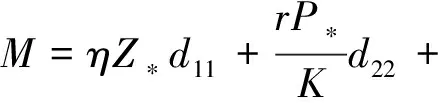
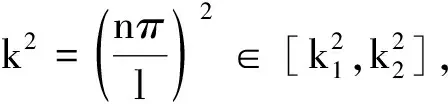
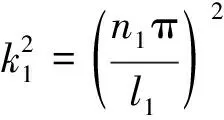
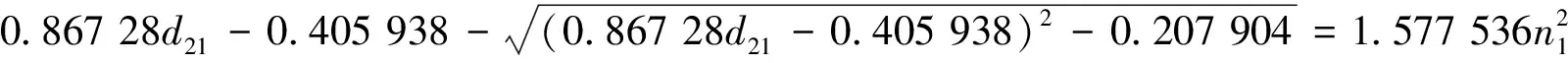
2 数值模拟
3 结 语

