解析独立性检验主观题型

■罗 铧

纵观近些年的高考数学题，我们发现多次出现了对独立性检验的综合应用题的考查，这也为我们的高考备考鸣响了警钟——不可忽视独立性检验综合应用题。下面具体分析。

一、独立性检验问题

要想解答独立性检验问题应做好两件事：一是准确解读2×2列联表，落实表中相关数据；二是正确利用公式求出K2的观测值k。

例1某部一连与二连展开各项战术技能比武，两个连队各选派了50名战士参加，规定比武成绩满分为100分，90分(包含90分)以上为优秀，90分以下为非优秀，比武结束后进行了成绩统计，得到两个连队战士比武成绩的2×2列联表，如表1，请回答下列问题。

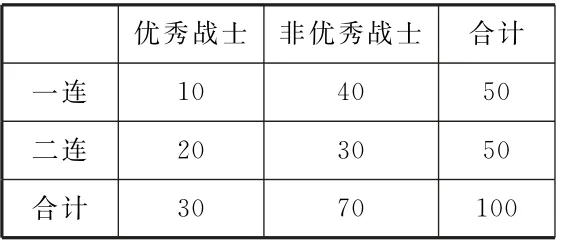
表1

(1)求K2的观测值k。

(2)判断是否有99%的把握认为“比武成绩与战士所在的连队有关系”。

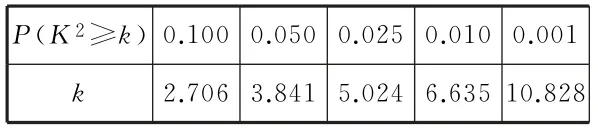
表2

解析：(1)由题意可得K2=，得k=4.762。

(2)因为K2≈4.762＜6.635，所以没有99%的把握认为“比武成绩与战士所在的连队有关系”。

二、独立性检验与频率分布直方图相交汇

在主观题中考查独立性检验一般是要渗透统计的其他知识，比如抽样方法、频率分布直方图、茎叶图等，而渗透这些统计知识的目的在于提供相关数据，来检验事件的独立性。

例2某电视台为了调查该地区观众对某一综艺节目的收视率情况，随机抽取了100名观众进行调查，其中女性观众有55人。图1是根据调查结果绘制的该地区观众每日平均收看该综艺节目时间的频率分布直方图。将日均收看该综艺节目时间不低于40min的观众称为“综艺迷”，根据统计得如表3所示的2×2列联表。

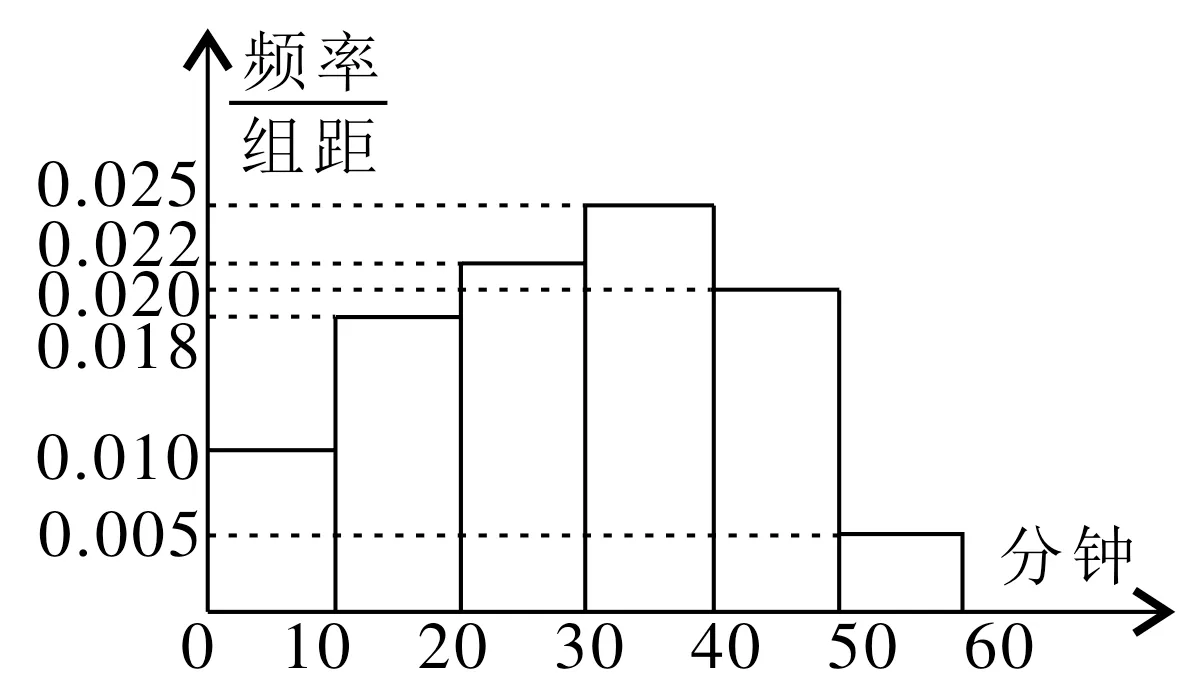
图1

表3

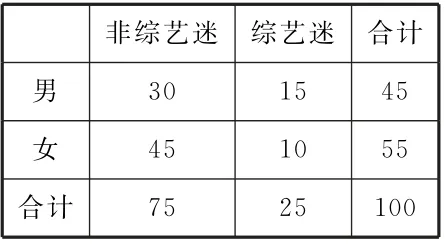
非综艺迷 综艺迷 合计男 30 15 45女 45 10 55合计 75 25 100

(1)判断是否有95% 的把握认为“综艺迷”与性别有关。

(2)把日均收看该综艺节目不低于50min的观众称为“超级综艺迷”，已知“超级综艺迷”中有2名是女性观众，若从“超级综艺迷”中任意选取2人，求至少有1名女性观众的概率。

解析：(1)由题意得K2=。因为3.030＜3.841，所以我们没有95%的把握认为“综艺迷”与性别有关。

(2)从频率分布直方图可得，“超级综艺迷”为5人，从而一切可能结果所组成的基本事件为(a1，a2)，(a1，a3)，(a2，a3)，(a1，b1)，(a1，b2)，(a2，b1)，(a2，b2)，(a3，b1)，(a3，b2)，(b1，b2)，其中ai表示男性，i=1，2，3，bj表示女性，j=1，2。由10 个基本事件组成，而且这些基本事件的出现是等可能的。用A表示“任选2 人中，至少有1 人是女性”这一事件，则A={(a1，b1)，(a1，b2)，(a2，b1)，(a2，b2)，(a3，b1)，(a3，b2)，(b1，b2)}，事件A由7个基本事件组成。因而。

备考指导：由此可知，我们在备考独立性检验问题时，应结合概率统计知识对独立性检验问题加以学习掌握，把二者交汇贯通，做到这一点，我们就不会再害怕高考中出现独立性检验主观题了。