老师搭台 学生唱戏
——例谈高中数学课堂中学生创造性思维的培养
■王兰灵
一、创造性思维及创造性思维培养的必要性
创造性思维指打破常规、具有创意、带有创新的思维。具有创造性思维的学生,观察力强,思维敏捷,逻辑缜密,能够更快速地认清问题的本质。他们能够更便捷地解决问题,甚至能对问题产生具有影响力的见解,进而丰富自身的数学思维,提升数学素养。高中阶段是学生思维和思想形成的黄金时期,创造性思维的培养在此阶段显得尤为必要。
二、例谈学生创造性思维的培养
学生的创造性思维,只能培养,不能灌输。基于这个理念,笔者尝试搭建了培养学生创造性思维的平台。在课前,布置适量的有利于培养学生创造性思维的习题,给他们足够的探究时间,鼓励学生独立思考,思考之后再互相交流。在课堂上,营造轻松和谐的氛围,鼓励大家对课堂的问题提出自己的见解,或者推荐优秀的解法。当解法巧妙时,就以学生的名字命名该解法。在课后,把学生的优秀解法记录下来,积累到一定程度后,形成论文,论文发表之后与学生一起分享其创造性的成果。将课前、课堂和课后三个环节综合起来,就形成了“老师搭台,学生唱戏”的创造性思维培养局面。现选取2020届高三12班(理科普通班)李乐恒、刘沛杰、戴志锴三位同学的三个案例跟大家一起分享。
案例一:“乐恒法”妙解“非线性”的线性规划题
例1已知变量x、y满足则目标函数的值域为_____。

图1
评注:该解法符合大部分学生的思维。根据目标式子的特点,联想到了向量的夹角公式,通过恒等变形,把目标式子转化成了2cos
解法2:乐恒法(极坐标法)。将x=ρcosθ,y=ρsinθ代入中,得z=,根据图1中可行域的位置,得,又因为cosθ和-sinθ在上都是单调递减的,所以代入端点值可快速求得结果。
评注:李乐恒同学的解法有两点被全班称赞。第一是他想到了极坐标,瞬间就把目标式子化简,变得简洁且熟悉;第二是他直接判断出了的单调性,而不是继续利用辅助角公式进行复杂化处理。这个解法非常新颖漂亮,很多经验丰富的老师都未必能想到这个处理方法。
案例二:“沛杰法”挑战函数法
例2已知函数f(x)=ex-1,g(x)=。若f(a)=g(b)成立,则b-a的最小值为_____。
解法1:常规解法(函数法)。令f(a)=g(b)=m,显然m>0。由得所以。记,,所以φ′(m)在(0,+∞)上单调递增。又,所以φ(m)在上单调递减,在上单调递增,即φ(m)的最小值为。
评注:函数法是大多数学生采用的方法,思路清晰,只要掌握了用导数研究函数单调性的技能,就能比较顺利地完成。
解法2:沛杰法(双等值法)。由得即为所求的最小值。
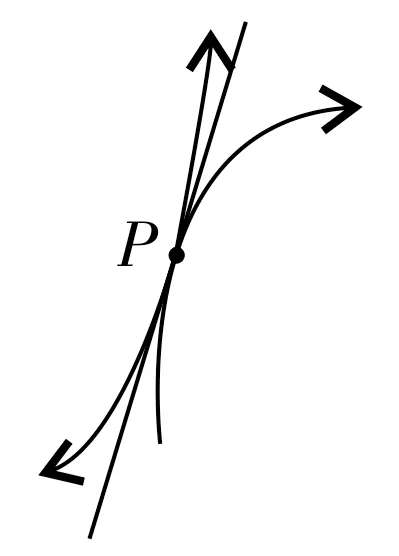
图2

图3
评注:该方法由刘沛杰同学提出,答案是正确的,但是课堂上他没有完全说清楚这种解法的理由。受沛杰同学的启发,经过课后的研究发现,这种双等值法(函数值和导数值均相等)是有根据的。如图2所示,两条“背靠背”的曲线相切时,它们有唯一的公切点P,也有唯一的公切线。当它们水平分开到某个值时,如图3所示,两条曲线水平距离的最小值是|P1P2|,其中P1和P2都是由公切点P水平移动衍生出来的。两条曲线在P1和P2处的切线与它们水平分开前的公切线平行。在本例中,因为f″(x)=ex-1>0,,所以f(x)的图像开口向上,g(x)的图像开口向下,两条曲线属于“背靠背”型,故沛杰同学的解法是正确的,而且解法简便,值得推广。
案例三:“志锴法”秒杀构造商函数法
例3已知定义在(0,+∞)上的函数f(x)恒为正数,f(x)满足f(x)<f′(x)<2f(x),则f(1)∶f(2)的取值范围是____。
解法1:常规解法(构造商函数)。由f(x)<f′(x)<2f(x)得f′(x)-f(x)>0,f′(x)-2f(x)<0。令,所以h′(x)>0,φ′(x)<0,得在(0,+∞)上h(x)单调递增,φ(x)单调递减。。
评注:该解法是根据f(x)<f′(x)<2f(x)而构造出和φ(x)=两个函数,利用这两个函数的单调性得出进而求得的范围。
解法2:志锴法(构造指数型函数)。根据f(x)<f′(x)<2f(x),设f(x)=enx,得f′(x)=nenx,代入f(x)<f′(x)<2f(x)中,得enx<nenx<2enx,化简得1<n<2,,因此。
评注:戴志锴同学的方法计算量小,方便快捷。戴志锴同学还说“看到了f(x)<f′(x)<2f(x)这个条件后,发现了导函数和原函数级别一样(可以比较),想到了函数y=ex,经过思考、修正之后,就发现了y=enx这个函数能够解决这类问题”。

