特征线法及其变体在水轮机及引水系统非线性建模中的对比研究

刘 冬，张 辉，任 刚，丁萁琦，陈 上，肖志怀

（1. 武汉大学 动力与机械学院，湖北 武汉 430072； 2. 武汉大学 水力机械过渡过程教育部重点实验室，湖北 武汉 430072；3. 中国长江电力股份有限公司 溪洛渡水力发电厂，云南 永善 657300）

1 研究背景

水轮机及引水系统构成的子系统是水轮机调节系统中的重要组成部分，蕴含着丰富的非线性动态特性，相关的建模理论研究一直以来都是行业研究的重点内容［1］。过去关于水轮机非线性模型的理论研究较多，而对于引水系统模型的研究则较少。在水轮机调节系统过渡过程仿真中，小波动情况下一般采用弹性或刚性水击模型，后者适用于长度较短的引水管道；大波动情况下采用经典的特征线模型［2］。实践证明，这些模型都能够在适用条件下以可接受的精度水平还原水轮机及引水系统的瞬时水压变化情况［3］。

引水系统的线性和非线性模型均是由描述有压管道内非恒定流的偏微分方程组推导得到的。刚性水击模型和弹性水击模型是通过将偏微分方程在稳定工况点附近线性展开得到的低阶简化模型，特征线模型则利用特征理论将偏微分方程转化为常微分方程，进而得到用于迭代计算的代数方程组［2-3］。为计算方便，在以上模型的推导中都不可避免地做出理想条件假设或忽略方程中的次要项。例如，通常假设管道的倾斜角度为零；近似认为水力摩阻恒定不变；不考虑损失项或对流项的影响［4］。

然而，基本特征线模型在实际应用中仍然存在一些问题，如对激波的捕捉能力不足［5］，水击波的振荡衰减速度慢［6］，采样周期无法任意调整［7］等。同时，在水电机组大波动仿真中，通常采用迭代法求解系统的非线性方程组，但迭代法的求解速度和稳定性很容易受到算法参数的影响［8］。此外，从模型可视化的角度来看，迭代法实际上是将水轮发电机组和引水系统作为整体进行求解，不利于子系统模型的使用和拓展［9］。

针对特征线模型的应用现状和实际仿真需求，本文提出了一种改进的特征线法，并基于该方法建立了计算方便且可视化程度高的水轮机及引水系统模块化非线性模型，同时搭建了用于基本特征线法计算的水轮机及引水系统联合非线性模型，以开展特征线法及其变体在水轮机及引水系统非线性建模中的对比研究。以国内某大型水电站机组孤网运行模式为例，基于水轮机及引水系统非线性模型，研究刚性和弹性水击模型、特征线法及其变体对水轮机调节系统大小波动过程仿真结果的影响，通过分析水轮机工作水头瞬时值的变化情况，总结各种模型的特点及其适用范围，为今后水轮机调节系统的大小波动仿真提供一定的理论指导。

2 特征线模型及其变体

2.1 基本特征线模型 基本特征线模型是通过求解有压管道非恒定流的偏微分方程建立的［2-3］。水力瞬变的基本方程包括运动方程和连续方程。当管道为水平或近似水平布置，同时考虑到对流项VVx和VHx相比其他项较小，可在数值计算中省略，则可得到一维简化水击方程组，如式（1）所示：

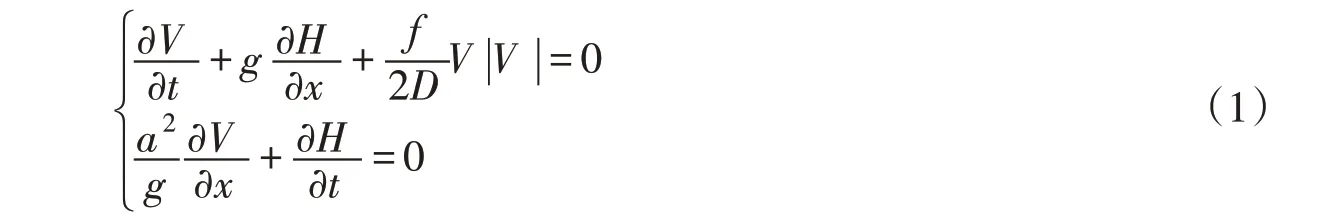
式中：V 为管道中水体的流速，m/s；H 为测压管水头，m； f 为摩擦系数； g 为重力加速度，m/s2；D 为管道直径，m；a 为水击波速，m/s；x 为自上游端开始计算的距离，m；

通过引入未知因子λ和微分法则，将偏微分方程组转化为全微分方程组，可解出特征值λ=±g a 。将其重新带入全微分方程组，即可得到两个特征线方程，如式（2）和式（3）所示：

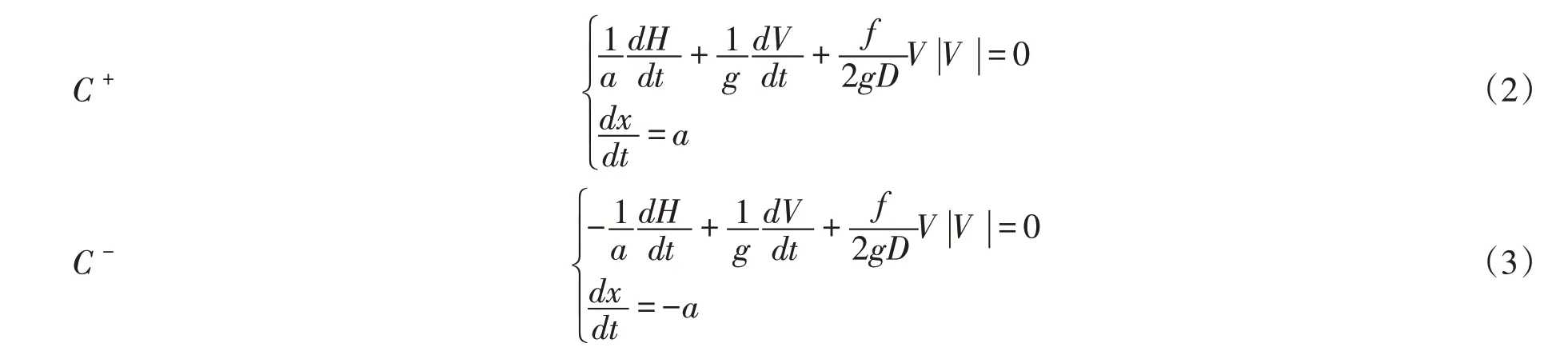
上述方程两边同时对x 进行积分，忽略二阶及以上高阶微量，得到管道内瞬变流在C+和C-方向上的代数方程，如式（4）和式（5）所示：

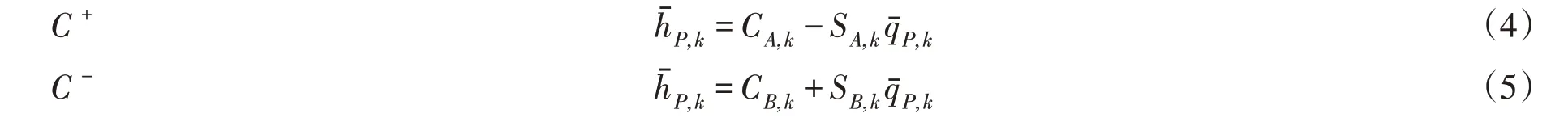
其中，下标A 、P 和B 分别表示某段管道左端、中间和右端节点处的变量和参数；下标k 表示当前时刻的变量和参数；和分别表示相对水头和相对流量；其他系数表达式分别为：

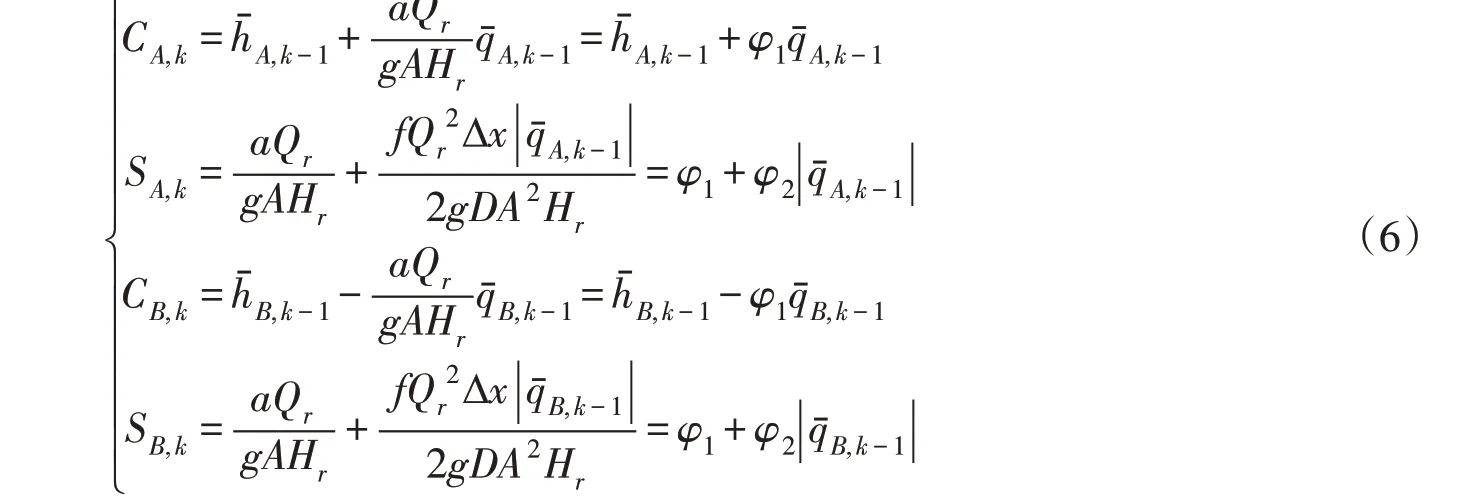
式中：Qr为水轮机额定流量，m3/s；Hr为水轮机额定水头，m； A 为管道截面积，m2；下标k-1表示上一时刻的变量和参数；φ1、φ2均为常数。

2.2 改进特征线模型一 为解决水击波的振荡衰减速度慢，采样周期无法任意调整的问题，文献［10］提出了加入水头反馈到流量和基于重采样技术的改进特征线法。该方法忽略了水头损失项（即常数φ2=0），且将有压引水管道分为单段，即上游水库端流量通过C-特征线方程求解，而蜗壳进口端水头通过C+特征线方程求解，相应的离散方程如式（7）和式（8）所示：

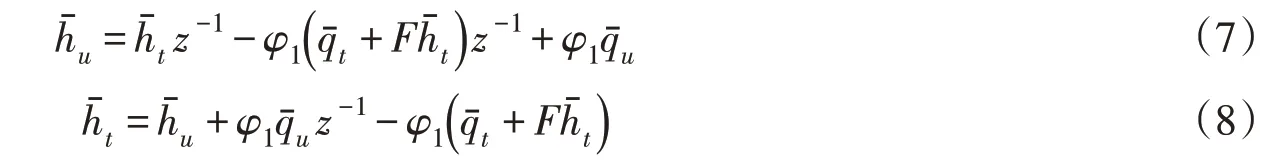
根据重采样理论，改变系统采样周期需要先将原离散系统转换为连续系统，再将该连续系统按新的采样周期离散化即可。为使转化前后系统的频率特性尽可能保持一致，转化方法采用双线型变换（即Tustin method）。由此得到重采样前后系统离散变量的函数关系，如下式：

式中：Tsn为新的采样周期；Tso为原系统的采样周期；z 、分别为重采样前后系统的离散变量。

将式（9）代入式（7）—式（8），并将变量的相对值化为偏差相对值，可得改进的特征线模型，如下式：

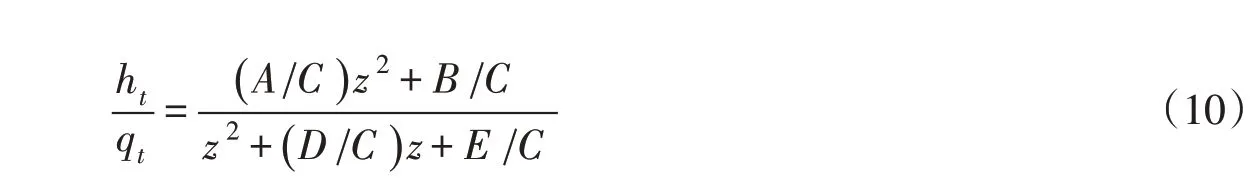
式中：ht和qt分别为水头和流量的偏差相对值，各系数的计算方法如下：

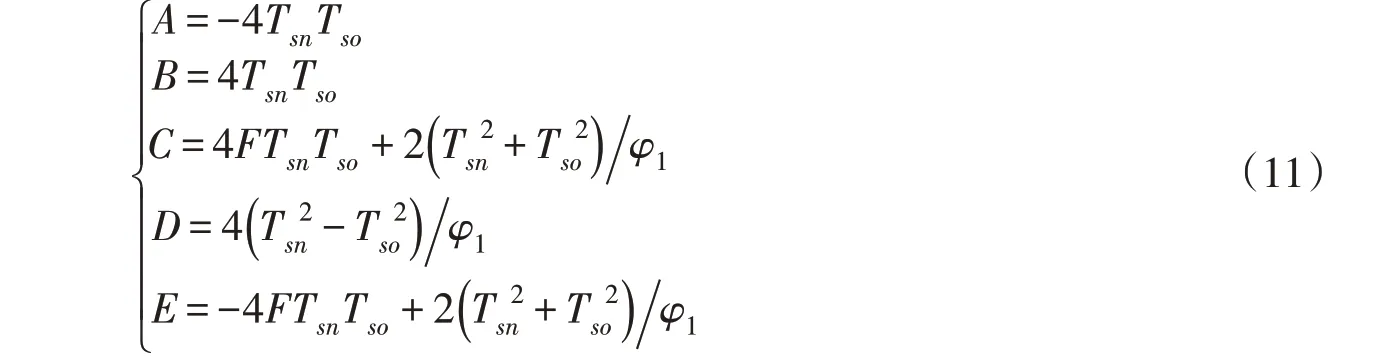
特别地，当F=0，即不考虑水头反馈时，该模型可理解为基于重采样的基本特征线模型。

2.3 改进特征线模型二 在基本特征线模型中，认为水力摩阻恒定不变。但研究表明，在水力瞬变过程中水力摩阻是非恒定的，且对水击压力瞬变过程具有重要影响［11-12］。IAB经验摩阻模型是一种重要的非恒定摩阻模型，它在原有恒定摩阻项Jq的基础上加入了非恒定摩阻项Ju，即水力摩阻变为［13］：

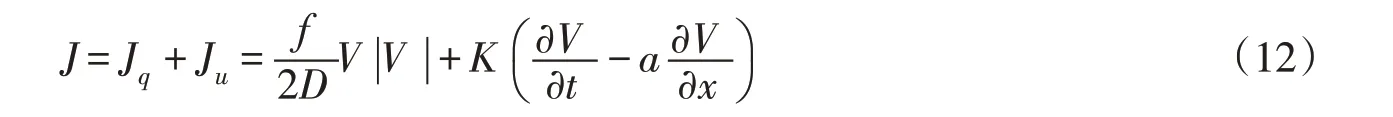
式中：K为Brunone摩阻系数，文献［14-15］给出了它的半经验半理论计算公式。

本文基于非恒定摩阻和重采样技术，提出了一种新的改进特征线法。首先将IAB 经验摩阻模型替换式（1）中的恒定摩阻项，并按照特征线法重新推导水击方程组，可解出特征值λ=( 0.5K±1) g a以及相应的两个特征线方程，如式（13）和式（14）所示：

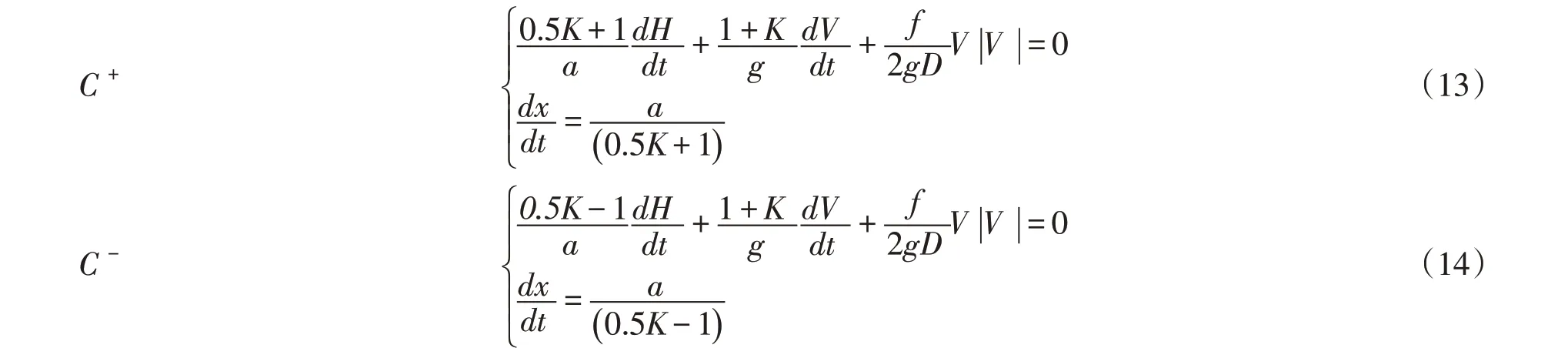
同理，上述方程两边同时对x 进行积分，忽略二阶及以上高阶微量，得到管道内瞬变流在C+和C-方向上的代数方程，其形式与式（4）和式（5）相同，但相应的系数变为：

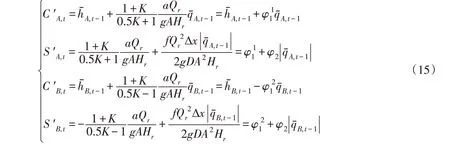
同样地，忽略水头损失项，且将有压引水管道分为单段，根据重采样理论，对系统进行相同的变换，得到另一种改进的特征线模型，其形式与式（10）相同，但相应的系数变为：

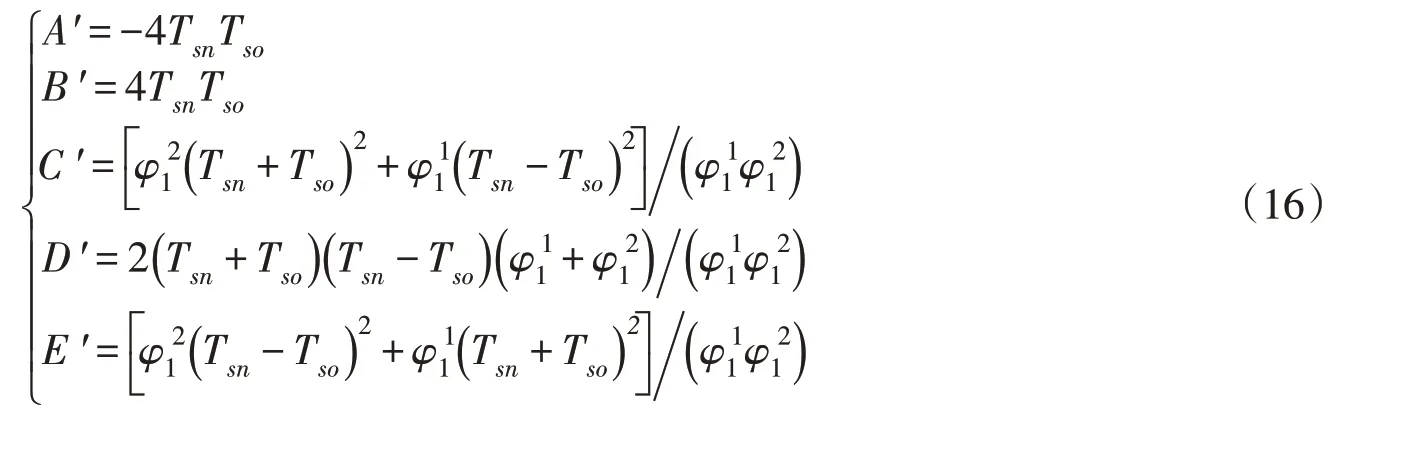
3 水轮机及引水系统非线性模型

3.1 联合非线性模型 基于引水系统基本特征线模型、水轮机神经网络模型和发电机一阶模型构成的联合非线性模型，再结合调速器非线性模型，可在MATLABSIMULINK 环境下搭建水轮机调节系统过渡过程的仿真试验平台，如图1—图3所示。图1中可通过设置给定值进行扰动模式切换（频率扰动和负荷扰动），图2的限幅环节和图3的限速环节在每个仿真步长内均需将当前变量由偏差相对值转化为绝对值后再进行计算。

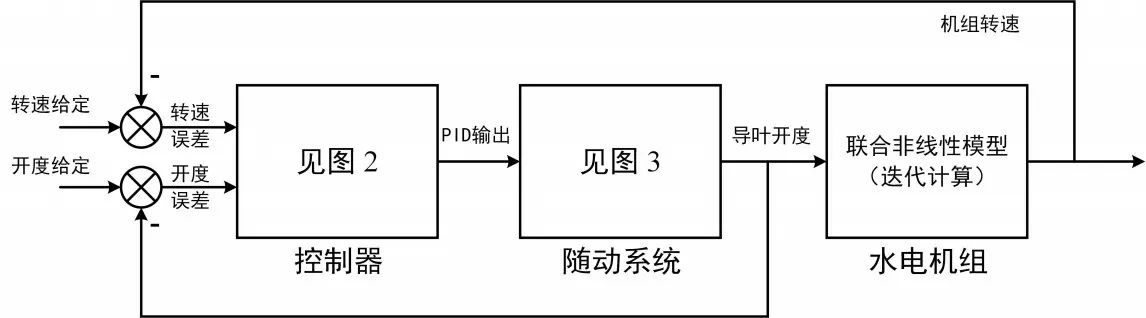
图1 基于水轮机及引水系统联合非线性模型的水轮机调节系统仿真平台

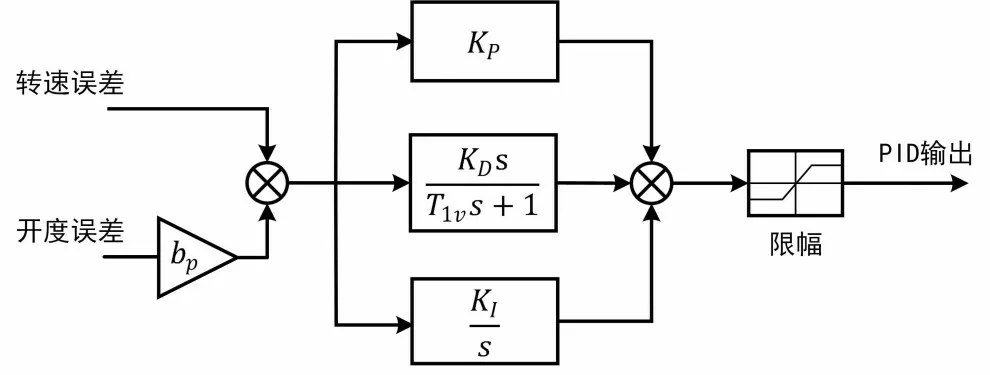
图2 水轮机调节系统仿真平台的控制器模型结构

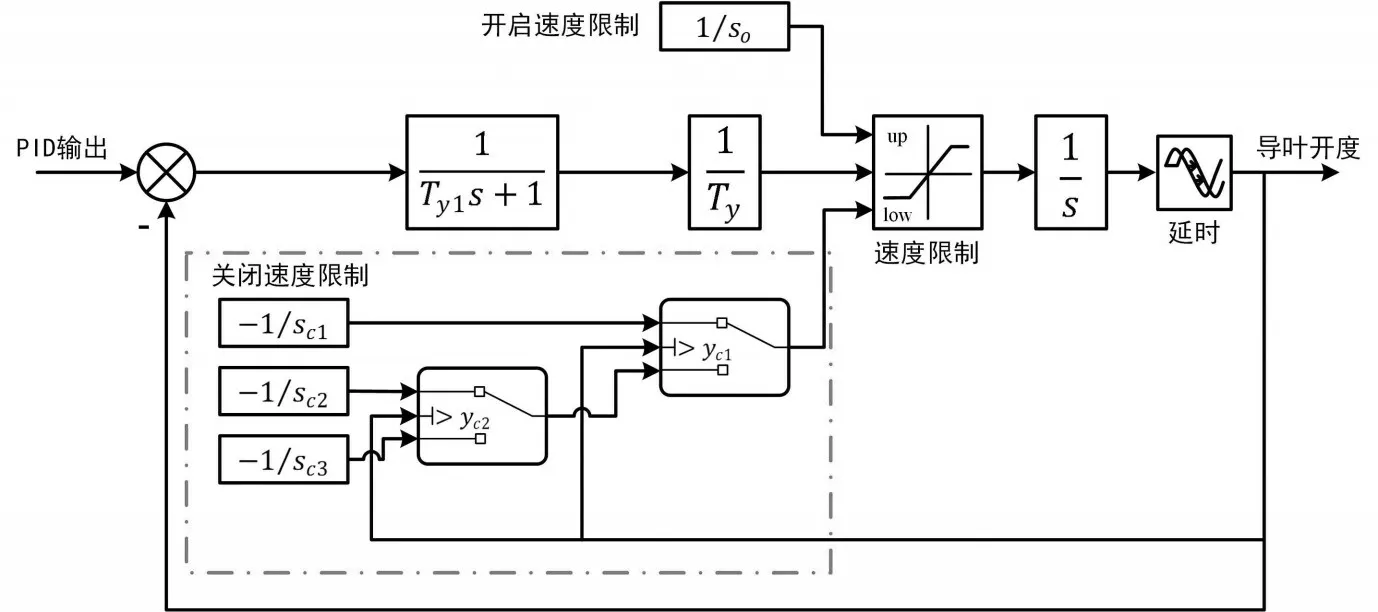
图3 水轮机调节系统仿真平台的随动系统模型结构

该平台中控制器模型采用并联PID 结构（其中参数KP、 KI和KD分别为比例、积分和微分增益；T1v为微分时间常数；bp为永态转差系数），随动系统模型包含中间接力器（其中参数Ty1为中间接力器反应时间常数，s）、主接力器（其中参数Ty为主接力器反应时间常数，s），导叶开启速度限制和分段关闭规律（其中参数so、sc1、sc2和sc3表示导叶开度从全关到全开需要的时间，s； yc1和yc2表示拐点处的导叶开度，%），以及输出限幅和延迟环节。在联合非线性模型中，水轮机非线性模型采用两个独立的神经网络，分别代表流量特性和力矩特性［16］。引水系统采用基本特征线模型（Charac⁃teristic line，简写为CL），发电机采用不考虑电气因素的一阶模型（其中参数Ta为机组惯性时间常数，s；eg为发电机负载自调节系数）。在仿真开始前，根据管道分段数确定采样周期，通过迭代计算确定水轮机初始水头和初始流量。在仿真过程中，每一采样周期内均需对水电机组联合非线性模型进行迭代计算，包括转速迭代和水头迭代两个部分，基本流程如图4所示［2］。

3.2 模块化非线性模型 模块化非线性模型是将水电机组联合非线性模型分离，将各子系统封装为独立的模块进行仿真，这样做的好处是在每个采样周期内避免了迭代计算，同时可视化效果好，便于模块的移植和重复利用。基于模块化非线性模型的水轮机调节系统在MATLABSIMULINK 环境下的整体结构如图5所示。

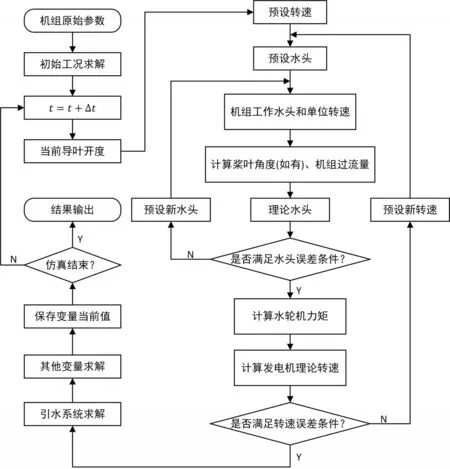
图4 水轮机调节系统过渡过程迭代计算的基本流程

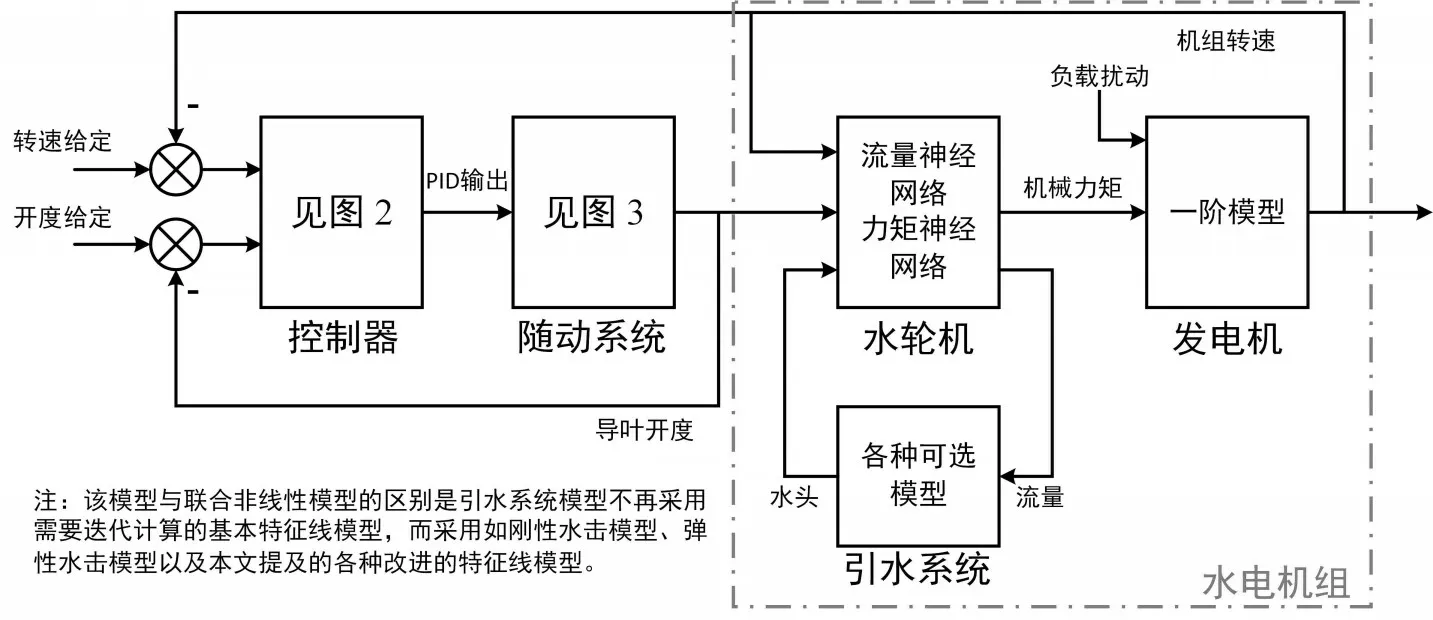
图5 基于水轮机及引水系统模块化非线性模型的水轮机调节系统仿真平台

由于采用了重采样技术，该平台的采样周期可根据需要任意设定。不同于联合非线性模型，引水系统模块不再采用需要迭代的基本特征线模型，而采用包含5种可选的非迭代模型，分别是刚性水击模型（Rigid water hammer，简写为RWH）、弹性水击模型（Elastic water hammer，简写为EWH）、基于重采样的基本特征线模型（Resampling-based characteristic line，简写为RCL）、基于重采样和水头反馈的改进特征线模型一（Improved characteristic line 1，简写为ICL1）和本文提出的基于重采样和非恒定摩阻的改进特征线模型二（Improved characteristic line 2，简写为ICL2），其他系统模块均与图1的对应部分保持一致。

4 仿真及对比研究

本文以国内某大型水电站机组为例，研究在孤网运行条件下，基于不同水击模型的非线性水轮机调节系统频率扰动响应和负载扰动响应（以基本特征线为参考进行分析）。图1 和图3 中的系统各部分详细计算参数如表1 所示。采用基本特征线法时，将管道分为20 段，采样周期由此确定为0.02 s［3］，采用其他非迭代方法时的采样周期均为0.01 s，所有方法的计算过程均不考虑水头损失。

水轮机调节系统的初始工况为：调速器运行在转速控制模式，初始开度为75%，初始水头为205 m，初始转速为125 r/min。在该工况下，分别进行频率扰动和负荷扰动（均包含大、小扰动），得到机组瞬时水头相对变化的过程曲线和最大绝对值（记为Hm），分别如图6和表2所示。

从图6可以看出，不同扰动条件下各种引水系统模型对于机组水头变化趋势的描述基本一致，仅在局部极值附近的计算结果有所差别，且在大波动条件下较为明显。局部放大来看，基于重采样技术的特征线法（RCL）和基本特征线法（CL）计算的水头变化存在一定误差，即RCL的Hm要小于CL的Hm，同时弹性水击模型（EWH）在大频率扰动时会出现水头的局部振荡现象。结合表2发现，在不同的扰动信号和扰动量下，比较非迭代方法计算的Hm，可以得出：（1）刚性水击模型（RWH）的Hm 最小；（2）RCL 的Hm 大于改进特征线法一（ICL1）但小于改进特征线法二（ICL2）；（3）Hm（CL）＞Hm（EWH）＞Hm（RCL）。

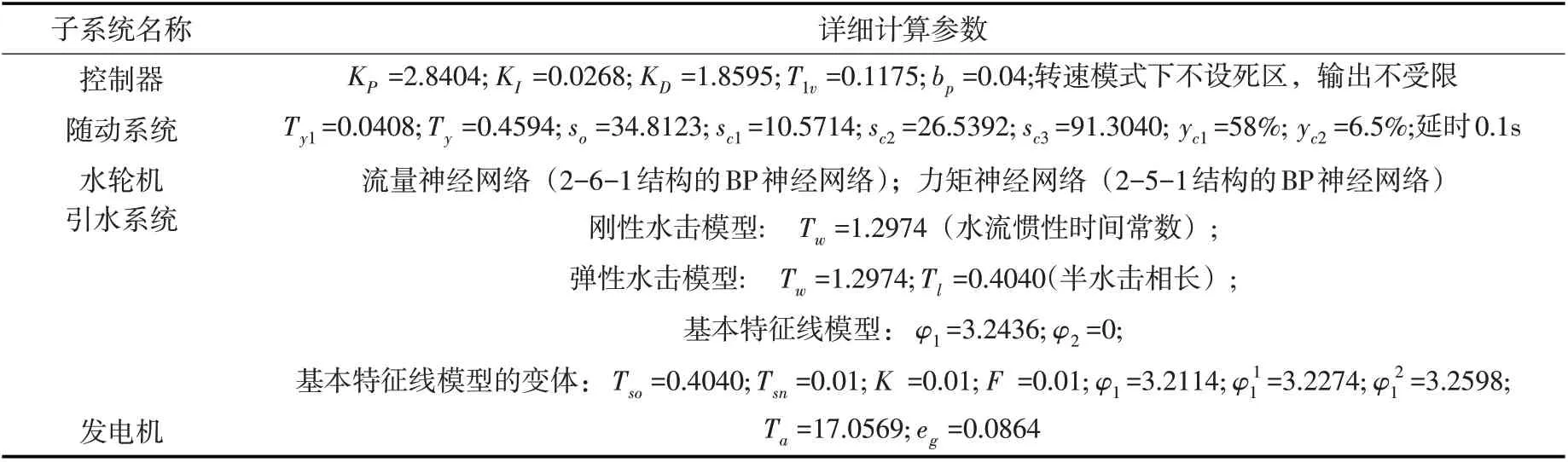
表1 非线性水轮机调节系统的详细计算参数

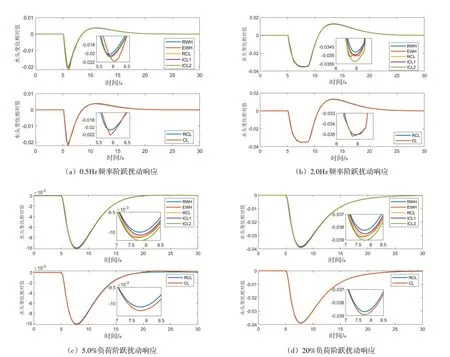
图6 不同频率和负荷扰动下机组水头的动态响应过程

表2 不同扰动信号下由各水击模型计算得到的Hm

在改进特征线模型一的基础上，改变水头反馈系数，观察机组瞬时水头相对变化情况并与基本特征线法进行对比，结果如图7（a）所示。在改进特征线模型二的基础上，改变Brunone摩阻系数，观察机组瞬时水头相对变化情况并与基本特征线法进行对比，结果如图7（b）所示。Hm随参数的变化关系如图8所示。

从图7可以看出，对于ICL1，随着水头反馈系数的增加，Hm逐渐减小，水头变化曲线整体向内收缩；对于ICL2，随着Brunone摩阻系数的增加，Hm逐渐增大，水头变化曲线整体向外扩张。当水头反馈系数或Brunone摩阻系数为零时，相应的改进特征线模型等价于RCL模型。

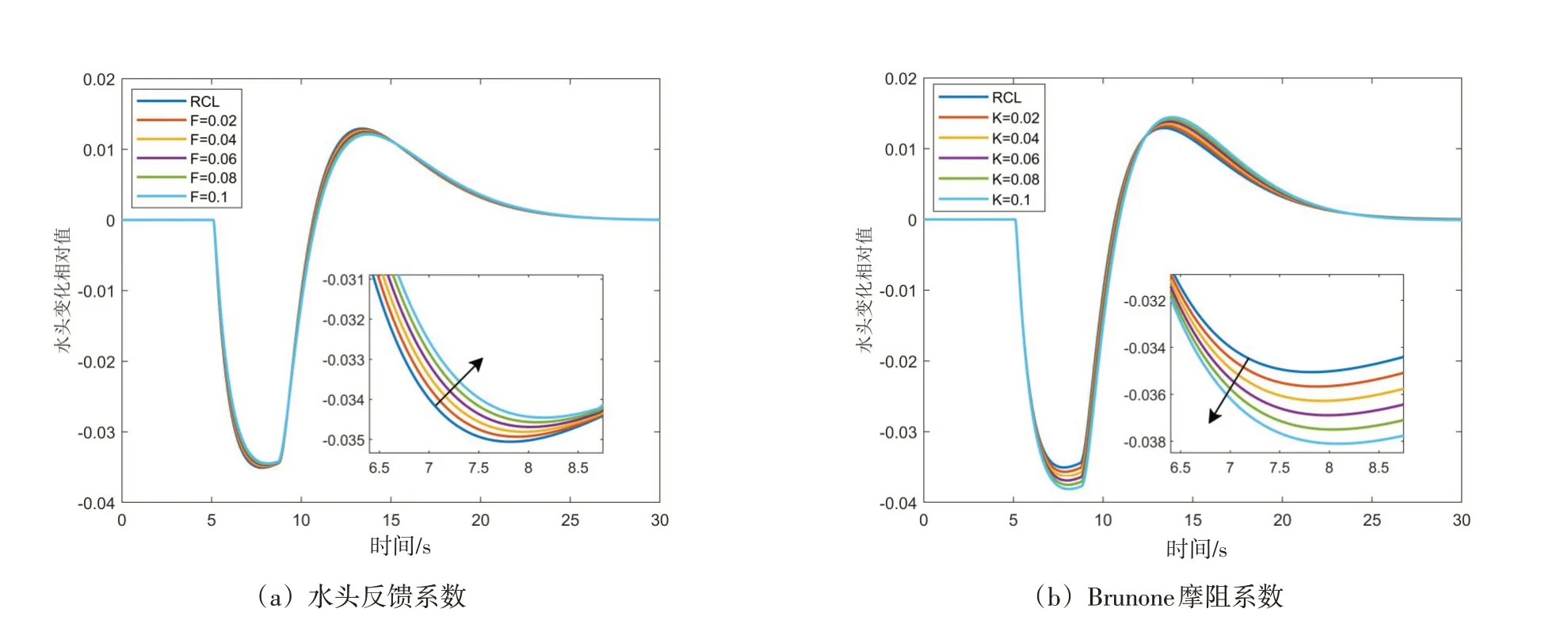
图7 参数变化时机组水头的动态响应过程（2.0Hz频率阶跃扰动响应）

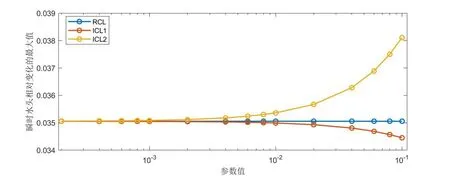
图8 Hm随不同参数的变化情况

从图8 可以看出，Hm 开始出现明显变化的临界参数值为F=0.01 和K=0.001。在同一参数范围内，Hm随参数K的变化速度明显快于其随参数F的变化速度，说明Hm对参数K的变化更为敏感。因此，在调节参数时K应当取较小值，而F 应当取较大值。

最后，针对所有基于特征线法的引水系统模型，研究两个基本参数φ1（φ1=Tw/Tl）和φ2对仿真结果的影响。在相同的初始工况和20%负荷阶跃扰动条件下采用基本特征线法，固定φ1改变φ2，得到的仿真结果如图9（a）所示。固定φ2改变φ2，得到的仿真结果如图9（b）所示。

从图9可以看出，随着φ1（与管径成反比）的增大，Hm逐渐变大，水头稳态值则不受影响；随着φ2（与摩擦系数、管径和单段管长有关）的增大，水头稳态值相对初始值逐渐减小（若为负扰则逐渐增大），Hm则基本不变。因此，在对引水系统进行建模时，可以根据实测数据并通过辨识的方法确定这两个基本参数。

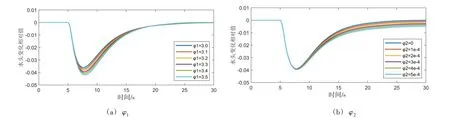
图9 引水管道基本参数对机组瞬时水头的影响

5 结论

本文在已有的引水系统基本模型的基础上，提出了改进的特征线法，建立了包含各部分详细结构和参数的水轮机调节系统联合非线性模型和模块化非线性模型。在此基础上，以机组孤网运行模式为例，在频率和负载的大、小扰动作用下，研究了刚性和弹性水击、特征线法及其变体模型的仿真结果之间的区别与联系。对仿真结果进行分析，可以得出以下主要结论：

（1）在适合的参数条件下，不同引水系统模型对于机组水头变化趋势的描述基本一致，仅在局部极值附近的计算结果有所差别，且在大波动条件下较为明显，但可通过调整具体的模型参数减小这种差别。

（2）由于改进的特征线模型二、基本特征线模型和弹性水击模型对机组瞬时水头最大变化的计算结果均大于基于重采样的基本特征线模型，因此当改进的特征线模型二的计算结果较大时，可通过减小参数K 使改进的特征线模型二的计算结果充分接近基本特征线模型或弹性水击模型，反之亦然。

（3）由于改进的特征线模型一和刚性水击模型对机组瞬时水头最大变化的计算结果均小于基于重采样的基本特征线模型，因此当改进的特征线模型一的计算结果较大时，可通过增大参数F使改进的特征线模型一的计算结果充分接近刚性水击模型，反之亦然。

（4）对于基于特征线法的引水系统模型，调整参数φ1能够改变水头变化的幅度，两者成正比关系，而调整φ2能够改变水头的稳态误差，两者成正比关系。