基于蒙特卡洛树搜索的土石方动态调配算法及验证
王仁超,张鹏程,徐跃明
(1. 天津大学 水利工程仿真与安全国家重点实验室,天津 300354;2. 中国电建集团 华东勘测设计研究院有限公司,浙江 杭州 311122)
1 问题提出
土石方调配是堆石坝等大型土建工程施工中的重要内容,制定合理的土石方调配方案对于降低工程造价、保证工程顺利实施具有重要的工程意义。土石方调配与建筑物施工进度、道路布置、料源料场设置等紧密相连且相互影响。传统的土石方调配[1]主要依靠设计人员在施工进度、料源料场设置、施工道路确定的前提下,规划各个时段土石方调运量,以确保挖、填平衡。1980年代以来,随着运筹学的发展,有些学者采用线性规划[2-4]、动态规划[5]等系统优化模型克服了土方累积图法的缺点,以运距最小为目标,优化各个时段土石方调运量。1990年代以来,随着系统科学、计算机科学的发展,有些学者尝试将粒子群算法[6-7]、蚂蚁算法[8]等群智能算法用于土石方调运优化问题,以解决模型中可能包含的非线性约束或目标关系。但总体而言,以往的土石方调配问题都假设开挖和填筑施工进度是确定的[9],这种土石方调配问题通常被称为土石方静态调配问题。
抽水蓄能电站由于施工场地狭窄、施工道路布置困难等,其大坝建设的土石方调配问题更为突出,开挖和填筑进度受水文、气象、地质等条件影响较大[10],工程实施过程中的进度和计划进度之间往往会出现一定偏差,土石方调配应根据进度变化做出实时调整,这种将填筑、开挖进度与土石方调配有机结合起来的问题通常被称为土石方动态调配问题,其目的是寻找满足一系列进度目标的土石方调运费用最小的施工方案。
针对土石方动态调配问题,使用常规的土石方静态调配方法往往需要花费较多时间重新规划填筑、开挖进度,难以满足工程实时控制的要求。目前常用的方法是计算机施工仿真技术,通过输入合理的施工参数和施工面貌信息,快速演绎实际施工过程,在短时间内进行多个施工方案的对比,为制定合理的施工方案提供了参考。然而,在应用现有施工仿真模型[11-13]进行施工进度控制和土石方调配时,会遇到以下问题:(1)形成一套土石方动态调配方案需要花费1到2个月的时间,无法做到真正的动态控制;(2)该方法需要使用者拥有丰富的工程仿真经验,包括优化、仿真建模经验;(3)计算结果包含的工程进度、资源、成本等工程控制关键信息隐含在模型和结果中,不便于工程设计、现场施工管理人员利用。
近年来,以深度学习和强化学习为代表的人工智能算法取得了惊人的发展。MCTS 算法首先出现在计算机围棋领域[14]并且取得了巨大成功,2016 年采用深度强化学习和MCTS 相结合的计算机围棋软件AlphaGo 以4∶1 的巨大优势战胜了围棋顶级职业选手李世石,刷新了人类对人工智能的认识[15],极大地推动了MCTS算法在游戏领域[16]、医疗领域[17]以及规划调度领域[18-20]的研究热潮。这些领域的研究表明MCTS算法对于序贯决策问题是一种强有力搜索算法并具有较好的适应性。
Alpha-Zero解决问题思路为:以当前对局双方形成的对弈局面为状态,通过MCTS搜索后续对弈的可能步序(期间假设对方也以最佳策略应对,这个过程称为自对弈),收集状态和策略数据用以训练策略价值网络,最后基于策略价值网络形成目前局势下的最佳对局步骤及其赢棋概率;不同的对弈局面会有不同的对弈策略以及相应的赢棋概率。本文针对土石方智能动态调配问题,在建模过程中首先将土石方动态调配离散化为多个时间阶段,将其转化为序贯决策问题;其次,以当前累计填筑工程量等为状态,用各月填筑工作面对应的填筑可达强度构造动作空间,综合考虑工期、坝面施工机械费和土石方调运费等构造奖励函数,实现类似Alpha-Zero 的自对弈过程,以搜索当前施工局面下后续时段的施工进度安排策略及可能的土石方调运方案,这些结果可以用于后续研究中策略价值网络的训练,以便在工程实施过程中实现智能动态控制,如给出后续进度安排计划以及评价某一阶段进度安排对于工期、费用目标的影响。由于本文主要探讨土石方智能动态调配MCTS方法,后续讨论将围绕MCTS算法展开,有关策略价值网络将在后续研究中进一步开展,后续算例中策略为人工选择价值最大的策略。
MCTS 算法具有以下优点使其十分适用于土石方动态调配问题:其一,对领域知识的依赖程度低。针对土石方动态调配问题,开发一个适合的启发式算法需要大量的领域知识和时间,有时甚至无法构造出一个可用的启发式算法,因此选用对领域知识依赖程度低的算法是有必要的。其二,非对称扩展。由于土石方动态调配问题的状态空间大,使用经典搜索算法求解,收敛速度会变慢且容易陷入局部最优,MCTS算法允许在搜索过程中偏向价值更高的节点,提高了搜索效率。
基于MCTS 算法对序贯决策问题的较好适应性及其优点,本文尝试将计算机围棋软件AlphaGo-Zero的核心算法框架——MCTS算法应用于土石方动态调配问题,提出一种新的土石方动态调配模型(Earthwork Dynamic Allocation Model,EDAM)。综合考虑填筑施工进度控制和土石方调配的特点,将改进的UCT算法和剪枝优化技术应用于MCTS。本文提出的EDAM可以根据填筑施工现状快速生成填筑进度计划,并基于该填筑进度计划,以运费最小为目标生成土石方调配策略,在工程项目整个实施过程中可以给施工管理人员和建设监理人员提供参考,有效减少施工管理人员因控制不当造成的时间和费用损失,从而提高工程的经济效益。
2 智能视角下的土石方动态调配问题分析与模型
2.1 土石方动态调配问题与计算机围棋问题的对比分析 土石方动态调配问题与计算机围棋问题有很多相似之处:(1)两个问题都属于情节性任务,即在有限步骤内会结束的任务;(2)两个问题都属于序贯决策问题;(3)两个模型中的动作不仅影响当前的即时回报,也会影响其后的状态以及累计回报。考虑这些相似之处,本文尝试使用MCTS算法解决土石方动态调配问题,并借鉴MCTS算法在计算机围棋软件AlphaGo-Zero中的应用。但是两个问题间也存在一定差异,为了使MCTS算法更贴合土石方动态调配问题,以下分析了两个问题的主要差异:(1)计算机围棋属于二人零和博弈问题,博弈双方具有严格的竞争关系;而土石方动态调配问题类似于单人游戏[16],系统决策者与环境之间不是对抗关系,而是一种相互影响的关系,因此本文改进了UCT算法。(2)在AlphaGo-Zero 对弈过程中,系统选择落子策略中赢棋概率最大的位置执行落子,对应落子位置的状态转移概率是1,执行落子的过程属于确定型决策过程;而在土石方动态调配问题中,环境中的不确定性因素会对进度计划的执行造成影响。(3)模拟结果范围有很大区别,计算机围棋模拟结果有三种:赢棋、平局、输棋,对应的奖励值为{1,0,-1};土石方动态调配由于评判标准的不同,其模拟结果的奖励值不再局限于[-1,1],但是MCTS要求节点平均分[21]保持在[-1,1]之间,因此需要将模拟结果进行数据标准化处理。
2.2 基于MCTS的土石方动态调运模型与假设 土石方动态调运与进度控制问题可以视为序贯决策过程,工程管理者基于当前填筑、开挖状态,确定未来一定时段内的进度计划,并配置一定的施工资源来实施进度计划。但是由于环境具有一定的不确定性,决策者拟定的进度计划在实施过程中会出现一定程度的滞后或提前。由于本文主要是为了验证基于MCTS的土石方动态调配方法的可行性,验证所用的比较对象为确定型仿真结果,计算机施工仿真模型中对于环境因素采用有效天数等平均统计方法概化,本文采用同样的方法概化环境因素,即依据计算机施工仿真采用有效天数概化环境因素,假设决策者决策将会按计划实施,后续状态为确定型的,这样就将土石方动态调配问题转化为确定型的单人决策问题。另外,现阶段为了简化问题还做了如下假设:依据施工组织设计手册和工程经验,假设填筑可达强度为填筑面等效长宽尺寸、有效施工天数的确定函数;依据模型所应用工程的特定条件,假设开挖对填筑不造成约束(对于开挖制约填筑情况,可以以开挖最大能力形成动作空间,故该假设不影响本文算法的合理性)。
基于MCTS的土石方动态调配模型(EDAM)包括状态空间、动作空间、奖励函数以及剪枝优化等方面,目前阶段,当实际进度与原始进度计划相比发生变化时,通过更新模型中的当前累计填筑工程量、当前月份信息以及工期目标等参数,来控制进度的动态变化。在后续研究完成策略价值网络的构建后,当工程工期控制目标不变时,可以直接由当前状态得到后续最佳策略。
(1)状态空间。状态空间中的每一个状态S都是一个三维特征向量,如第i阶段状态Si=(Vi,Ai-1,Mi),其中Vi代表第i阶段初累计填筑工程量,Ai-1代表第i-1阶段选择的计划月填筑工程量,Mi代表第i阶段对应的月份信息。如此来描述状态是因为在填筑形式确定的情况下,Vi可以反映第i阶段的填筑面貌,Ai-1的设定可以约束第i阶段的计划月填筑工程量,Mi可以反映当前月份对应的有效施工天数,以表示天气对施工的影响。
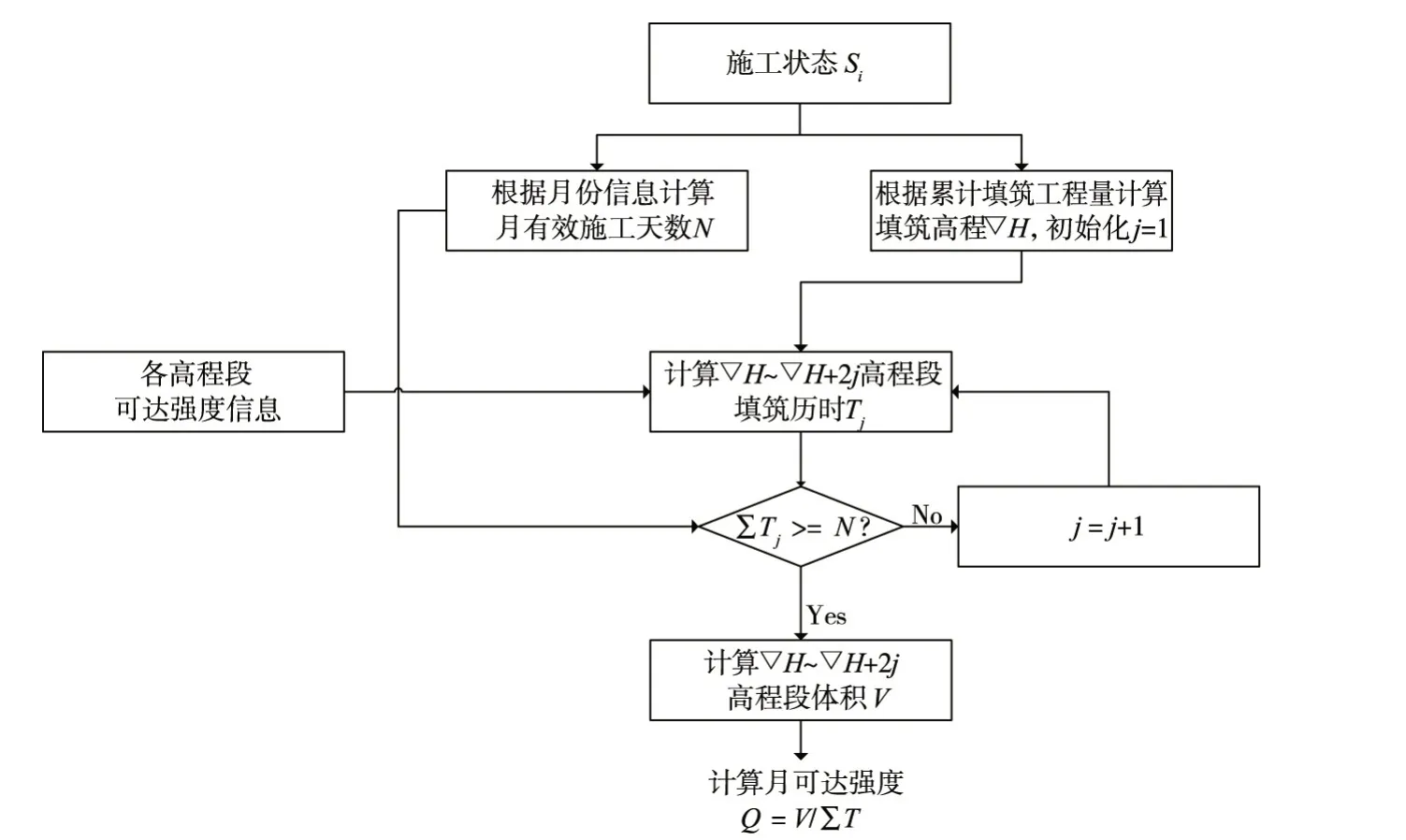
图1 月可达强度确定方法
(2)动作空间。在本文提出的EDAM中,动作是计划月填筑工程量,考虑连续的动作空间太大会导致运算速度变慢,本文将动作空间离散化。动作空间离散化需要考虑两个问题,一是计划月填筑工程量的上限是多少,二是计划月填筑工程量的精度取多少。对于第一个问题,本文将计划月填筑工程量的上限称为月可达强度Q。参考王仁超等[11]提出的坝面可达强度概念,把一个填筑子区按高程划分为若干高程段,对每个高程段,根据高程段上下工作面尺寸、坝面作业组织方式、机械类型和卸料点数量等因素确定各个高程段的坝面填筑强度。基于以上的概念,Q的计算过程如图1所示。对于第二个问题,离散的精度决定了调配效果:精度越高,动作空间越大、调配效果越好,但系统计算量也会变大、运算速度会变慢。考虑实际工程中土石方调配情况,本文选取104m3作为动作空间的离散精度。
(3)奖励函数。在EDAM模型中,奖励函数主要包含两部分:进度奖励、施工费用。其中进度奖励包含总进度奖励r1、阶段进度目标奖励r2;施工费用包含坝面施工机械费用r3、土石方调配费用r4。本文提出的奖励函数具体如下:
①总进度奖励r1。项目的正常工期为TP,EDAM模拟项目工期为TS,△T=TP-TS。若△T>0则模拟项目提前完工,系统会有提前完工奖励以及压缩工期需要的赶工费用,如图2所示;若△T <0则模拟项目不能按时完工,系统会有滞后惩罚。综合考虑按时完工奖励、提前完工奖励、赶工费用以及工程滞后惩罚等因素,总进度奖励r1与工期的关系示意图如图3所示。

图2 提前完工时间与奖励、费用关系

图3 r1与工期的关系示意图
②阶段进度目标奖励r2。根据工程项目的节点工期设置系统的阶段进度目标,若按期完成阶段进度目标奖励r2加1分。
③坝面施工机械费用r3。根据各月计划填筑工程量以及填筑工作面尺寸,统计各月需要租用的填筑设备数量,本文假设每套填筑设备每月租用费用为1,计算填筑进度计划对应的坝面施工机械费用。
④土石方调配费用r4。根据不同填筑期的道路布置情况以及土石方流信息,测量各开挖区料物到对应填筑子区的运输距离。在运输距离的基础上,综合考虑天气情况、运输强度和物价波动对道路运输费用的影响,制定综合运输单价。构建土石方调配线性规划模型,求解填筑进度计划对应的土石方调配费用r4。
对r1、r2、r3和r4分别进行归一化处理,再按照0.25∶0.25∶0.25∶0.25的权重(具体权重指标可以根据工程实际情况确定)合成一个综合指标r,EDAM模拟结果的处理过程如图4所示。
(4)剪枝优化。剪枝优化是指通过领域知识“剪去”搜索树中不必要遍历的支路,提高动作选择的质量,优化程序的搜索效率。在工程实际施工过程中,短时间内人员配置、机械配置以及道路情况基本保持一致,因此相邻月份的填筑强度变化幅度不会太大,本文以相邻月份填筑强度约束作为领域知识进行剪枝。实际施工中填筑强度会有先上升、再平稳、后下降的趋势,为了使MCTS模拟有类似填筑趋势,在填筑前、中、后期使用不同比例的相邻月份强度约束区间。
3 蒙特卡洛树搜索算法及其改进
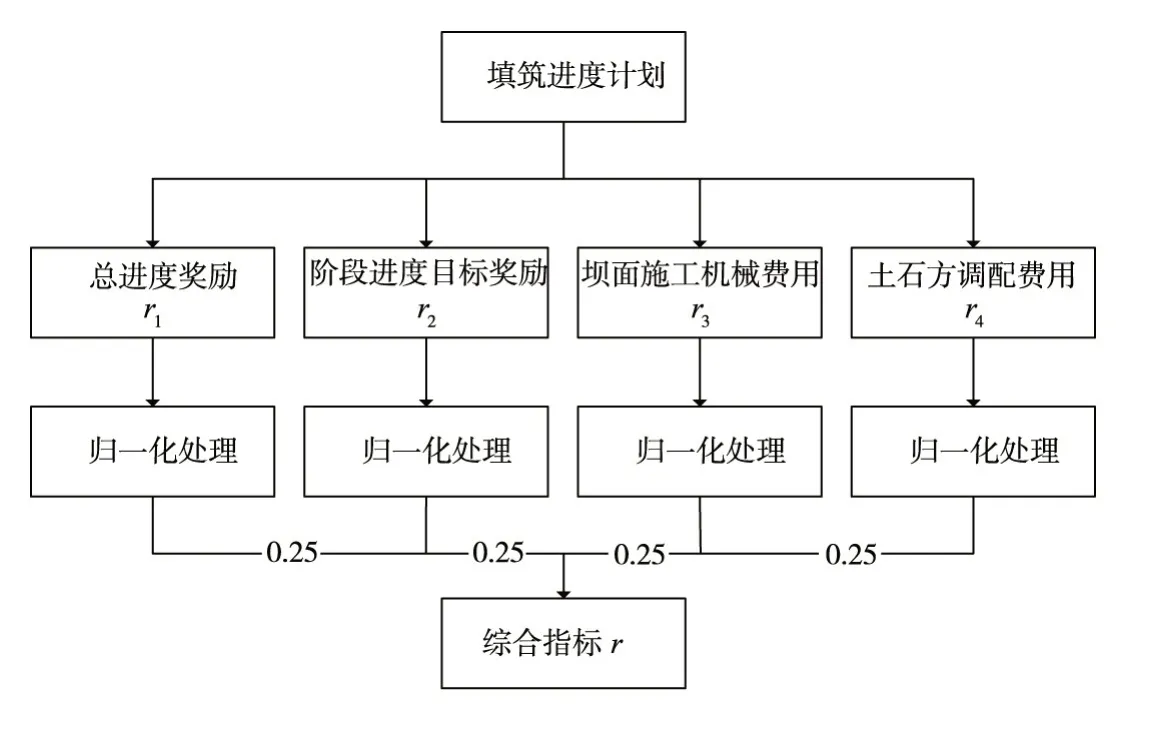
图4 模拟结果的处理过程
3.1 传统的MCTS 算法 MCTS 是一种通过随机抽样逼近实际结果的统计算法,在拥有很少领域知识的情况下仍然有很好的表现。MCTS利用蒙特卡洛模拟构建搜索树,可将树搜索的精度和随机抽样的多样性充分结合[21]。搜索树中每个节点代表一种状态,节点上储存了访问次数、奖励值等信息。节点与节点之间的连线代表一个动作,通过“节点→节点间连线→节点”模拟了系统状态转移过程。
MCTS 的搜索寻优过程由选择、扩展、模拟、反向传播4 个步骤构成,这4 个步骤会迭代执行,直到搜索时间用完为止,迭代搜索过程如图5所示,最终选择状态对应的最优动作。

图5 MCTS的迭代搜索过程
(1)选择步骤。在MCTS算法中,由于动作选择具有一定的随机性,平均奖励值最高的动作不一定最优,需要使用树策略平衡选择过程中的探索和利用。探索是指选择平均奖励值低而且访问次数较少的节点,以获取有关该节点的更多信息,探索有可能寻找到更好的动作,但过多地依赖探索会导致算法学习率过低;而利用是指选择当前统计结果中平均奖励值最高的节点,当不确定性导致计划实施与预期不符时,平均值越高,最终的结果越稳定,但过多地依赖利用会导致算法陷入局部最优。为了有效地解决“探索-利用”矛盾,Kocsis 等[22]选择UCB1作为树策略,提出UCT算法来平衡选择过程中的探索和利用,UCT算法的基本公式如式(1)所示。从根节点开始,在计算出各节点的UCT指标值后,依次选取UCT指标值最大的节点进行搜索,搜索选到待扩展节点为止。

(2)扩展步骤。根据待扩展节点上的状态信息计算动作选择空间,从可选动作列表中随机选择没有访问过的动作进行状态转移,在搜索树中扩展一个新节点储存新的状态信息。
(3)模拟步骤。从扩展的子节点起,利用默认策略一直模拟到游戏最后,得到相关奖励值。常用的默认策略是随机选择策略。
(4)反向传播步骤。从扩展节点起,向上回溯至根节点为止,更新搜索路径上各节点信息,包括节点访问次数,节点平均奖励值,更新公式如式(2)、式(3)所示。

式中,∑Qi表示节点i上所有模拟结果之和。
重复选择、扩展、模拟、反向传播这4个步骤,直到搜索时间用完为止。接下来,按照不同策略选择最终执行的动作,本文将对比以下三种选择策略:(1)选择平均奖励值最高的子节点;(2)统计各子节点的最高奖励值,选择最高奖励值最大的子节点;(3)选择访问次数最多的子节点。


3.3 算法流程 本节给出改进的MCTS 迭代搜索流程,流程图如图6 所示,算法搜索的具体步骤如下:
步骤1。初始化系统,创建根节点,选择根节点作为当前节点。
步骤2。计算当前状态的可选动作范围。
步骤3。判断当前节点是否完全扩展。若没有完全扩展,随机扩展子节点;若完全扩展,根据改进的UCT公式,计算各子节点的价值,选择价值最高的子节点作为当前节点,重复步骤2-3。
步骤4。从扩展节点开始随机模拟,直到终止状态。
步骤5。将终止状态输入评价模块,计算得到本次模拟的奖励值。
步骤6。反向依次更新父节点信息,包括节点访问次数和奖励值信息。
步骤7。判断是否完成阶段迭代次数,若没有完成阶段迭代次数,则重复步骤2-6;若完成阶段迭代次数,则根据最优动作选择策略,选择最优子节点。
步骤8。判断最优子节点是否为叶子节点,若是叶子节点,则模拟结束、输出最终结果。若不是叶子节点,则将该最优子节点作为当前节点,并重复步骤2-6。

图6 改进的MCTS迭代搜索流程图
4 工程实例验证
4.1 工程概况 某抽水蓄能电站位于江苏省,其上水库大坝为面板堆石坝,坝顶高程为269.4 m,总填筑方量约为2793.98×104m3(填筑方),其中上游堆石填筑方量约为775×104m3,大坝填筑分为7期,填筑最佳工期为50个月。坝体上游堆石填筑主要来源于库盆A区、C区开挖料,下游堆石以及库底填筑主要来源于库盆B区开挖料。大坝填筑开始时间为2018年9月30日,工程控制2019年4月30 日前完成大坝132 m 高程以下填筑,预计2021 年5 月31 日前完成大坝234 m 高程以下填筑、2022年11 月30 日前完成大坝整体填筑。截止2019 年12 月末,上水库主坝上游堆石累计填筑方量为171.93×104m3,与进度计划相比滞后了51×104m3。上游、下游堆石填筑区允许交叉分段流水,库盆填筑不允许交叉分段流水,流水段内有摊铺、碾压、质检3道工艺。根据工程所在地近十年的天气统计数据,每年的5至10月需要考虑雨水对道路运输费用的影响,1月需要考虑雨雪对道路运输费用的影响。
选取上游堆石填筑子区数据验证本文提出EDAM 的有效性,若未加说明每组实验平行运行50次,每个阶段进行500次MCTS迭代,实验结果的评价指标为奖励值的平均值和标准差。
4.2 参数选择 式(1)中Cp取为 2 2[23],为了确定式(2)中偏差常数项D 的取值,本节设计7组不同D值的平行实验,实验选择考虑偏差的UCT算法作为MCTS的树搜索策略,选择节点平均分作为最终动作选择的依据。实验结果如表1所示,偏差常数项D设置为0.1,模型模拟的平均分最高、标准差最小,表明这样设置参数可以保障算法的寻优质量,而且算法的稳定性最好。因此在剩余的实验中,将Cp设置为 2 2,D设置为0.1。
4.3 不同最终动作选择策略结果对比分析 本节测试了三种最终动作选择策略的优劣:(1)最高平均奖励值;(2)最高奖励值;(3)访问次数最多。本节设计了三组平行实验,实验选择改进的UCT算法作为MCTS的树搜索策略,实验结果如表2所示,使用节点最高奖励值作为动作选择依据的结果要优于其它两种策略。因为即使搜索过程中只有一次模拟得到最高分,系统也会依次选择动作直到获得这个最高分,这样避免了较差模拟结果带来的影响。在剩余的实验中,将节点最高奖励值设置为最终动作选择的依据。

表1 参数D对算法性能的影响
4.4 与传统MCTS 算法结果对比分析 本节测试了3个版本MCTS的性能,其中MCTS(1)使用常规UCT 算法;MCTS(2)使用考虑偏差的UCT算法;EDAM 使用本文提出的改进UCT 算法。本节设计了对比实验,结果如表3所示,EDAM结果的平均分是3 组实验中最高的,偏差也是最小的,说明对于土石方动态调配问题,使用改进UCT算法的MCTS在算法的质量和稳定性方面要优于传统MCTS。在剩余的实验中,将使用改进的UCT算法作为MCTS的树搜索策略。
4.5 与计算机仿真模拟结果对比分析 近二十年,在常规水电工程施工组织设计中发展起来的以群智能算法为基础的填筑程序优化[24]、以计算机仿真为基础的坝体填筑施工仿真[11]和开挖施工仿真[13]以及以线性规划为基础的土石方调配是土石方动态调配基本方法。本节将计算机施工仿真模型与本文提出的EDAM 进行对比,两种模型生成的填筑进度计划如图7 所示,对应的奖励值如表4 所示,EDAM生成土石方调配方案如图8所示。

表2 不同最终动作选择策略结果对比
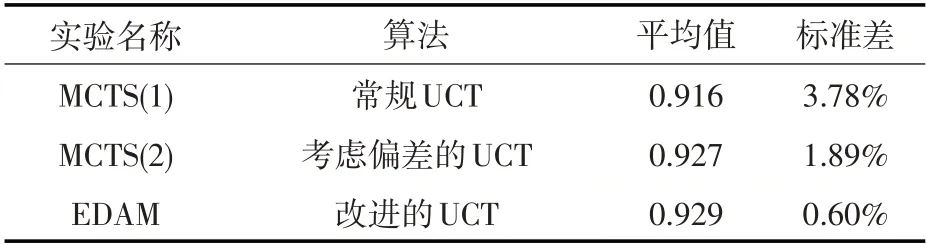
表3 EDAM与传统MCTS对比

图7 施工仿真与土石方动态调配模型结果对比
从图7 和表4 可以看出,EDAM 模拟结果与计算机施工仿真结果相比:(1)除了少数月份填筑强度有少许差异,两者的填筑趋势基本相同;(2)两者都在最佳工期内完成上游堆石填筑,都保证了项目的节点工期;(3)EDAM 的坝面施工机械费用以及土石方调配费用更少;(4)计算分析时间缩短,可以满足生产实践对时效性的要求。
4.6 土石方动态调配实例 从图9可以看出,与初期生成的填筑进度计划相比,截止2019年末上游堆石已完成填筑工程量滞后了51×104m3。在节点工期和总工期目标不变的情况下,调整EDAM模型中的初始状态变量进行土石方动态调配分析,基于2019年末施工状况EDAM模型生成的后期填筑进度计划如图9中白色柱状图所示,相应的土石方调配方案如图10所示。
工程滞后主要原因是不利的气象条件、地质条件以及施工管理人为因素等,目前现场已经改善了施工道路、处理了右岸坝肩不稳定区域,为后期赶工创造了条件。从图9中可以看出,滞后的工程量将在填筑高峰期内(2020年1月至2021年6月)完成赶工,2020年1月至3月填筑强度低于原进度计划是因为模型中有相邻月份填筑强度约束,填筑强度逐渐增强;2020年4月至2021年6月填筑强度高于原进度计划,是因为在节点工期的约束下主坝最大工作面(在175 ~200高程区间)处于该阶段,

图8 EDAM生成的土石方动态调配方案

表4 计算机施工仿真与EDAM的模拟结果对比

图9 土石方动态调配结果
注:计算分析用时是指,计算模型边界条件、调整模型参数、模型仿真计算和结果分析等花费时间的总和。该阶段填筑可达强度高,具备高强度施工条件,后期随着坝体上升工作面面积急剧减少不具备赶工条件,因此结果是合理的。从图11可以看出,与2020年度计算机仿真结果比较,两者生成的填筑进度计划趋势基本一致,进一步验证了模型结果的合理性。
5 结论与展望
本文受AlphaGo-Zero 思想启发,提出一种新的土石方动态调配模型EDAM,并将其应用于江苏省某抽水蓄能电站上水库主坝填筑分析。通过与传统计算机施工仿真模型的结果进行比较,可以看出:基于MCTS的土石方动态调配模型可以得到与传统计算机仿真模型趋势基本一致的结果,验证了该模型和方法的有效性。与传统计算机施工仿真模型相比,EDAM 减少了计算分析时间,且不需要决策者具有大量相关施工经验以及对相关工程的深入了解,可有效提高工程控制、土石方调配决策效率。针对堆石坝填筑进度控制和土石方动态调配的特点,对MCTS 算法中UCT 算法和剪枝优化技术做了改进,提升了算法的搜索效率和稳定性。

图10 上游堆石剩余工程量的土石方调配方案

图11 2020年度计算机施工仿真与EDAM结果对比
本文提出的EDAM模型是在土石方动态调配领域的初步探索,在后续研究中还需要做进一步扩展和改进:为了分析土石方动态调配策略对后期施工的影响,下一步将结合深度神经网络构建策略价值评价体系;为了提高填筑可达强度的计算精度,下一步将探讨不规则工作面对填筑可达强度的影响以及探讨多个填筑子区填筑进度相互协调、开挖起控制作用的情况以及环境不确定性带来的影响等。

