基于颗粒级配参数描述砂土持水及非饱和强度特性的土壤转换函数

张 昭，程靖轩，刘奉银，齐吉琳

（1. 西安理工大学 岩土工程研究所，陕西 西安 710048；2. 北京建筑大学 土木与交通工程学院，北京 100044）

1 研究背景

土的持水特性可用持水曲线描述，不仅是非饱和土水力特性的重要组成部分，而且在表征力-水耦合效应时发挥了核心作用。依据文献［1-2］，持水曲线与颗粒级配曲线、颗粒组成、干密度（或孔隙比）之间的关系可用土壤转换函数描述。黏土因其黏粒含量或有机质含量很高而在颗粒间会产生复杂的物理-化学相互作用，其微观结构非常复杂、干密度变化显著，然而，砂土因其干密度变化范围相对较小而可采用颗粒级配曲线快速、合理地预测其持水曲线。

土的非饱和强度特性在土坡稳定性评价以及路基设计过程中至关重要。已有学者以非饱和砂土为研究对象，在抗剪强度的试验规律［3-5］与其理论表达式［6-8］、抗拉强度［9-11］或黏聚作用机理［12］等方面取得了很多有价值的研究成果。依据文献［8，13-14］可知，非饱和强度特性与饱和度或基质吸力密切相关，在持水曲线上一定基质吸力对应的饱和度（或有效饱和度）可嵌入强度公式中。由此可见，若能利用砂土的颗粒级配参数预测其持水曲线，则可进一步估算在给定饱和度或基质吸力下的非饱和强度。这种方法对早期尚未测得试验数据的非饱和土工程中具有应用前景。

关于持水曲线的预测，若从半物理-半经验角度出发，一般假定土颗粒为球体颗粒，其间孔隙简化为圆柱形孔隙。Arya等［15］通过假定土颗粒级配曲线由若干单一粒组构成（每个粒组可按不同权重描述相应的土孔径分布），通过引入比例缩放系数，提出了基于颗粒级配曲线预测持水曲线的半物理-半经验模型（即AP模型）。随后，学者们通过改进土颗粒级配曲线［16-18］和比例缩放系数［19-21］的数学表达式对AP模型进行修正。另一种基于土颗粒级配曲线预测持水曲线的纯统计模型以土壤转换函数为基础，基于统计分析建立土颗粒级配参数与持水曲线模型参数的统计关系：Saxton 等［1］和Vereecken等［2］将土颗粒含量与模型参数建立关系；随后Scheinost 等［22］和Schaap 等［23］基于平均粒径和粒径均匀性预测持水曲线模型参数；Chiu等［24］采用贝叶斯概率原理，选取最优的数学表达式以改进土壤转换函数的预测精度。

半物理-半经验模型虽考虑了土的物理性质，但均以简化假定为理论基础，不可避免地引入经验参数，而且所需测定的参数较多，从而降低了在岩土工程实际中的应用性，而工程实际中对参数的快速估算仅需满足设计精度即可。纯统计模型虽可快速预测持水曲线，但缺乏物理内涵，且对构建统计关系的数据库之外的持水试验结果预测适用性局限。

为此，面向广泛应用的van Genuchten持水曲线模型［25］（简称VG模型），将砂土的基本物理特征融入统计分析中，以量纲分析法为基础，依据土颗粒级配分布分别考虑完全均匀和完全分散两种理想排列条件，描述持水曲线与颗粒级配参数的关系；对4种砂土进行补充持水试验，将其试验结果与非饱和土水力特性数据库（UNSODA）［26］中70 个砂土样的边界减湿持水实测数据相结合进行回归分析，采用控制粒径d60和不均匀系数Cu与VG模型参数a和n构建土壤转换函数；对土壤转换函数进行验证后，结合Lu等［27］推得的有效应力表达式，构建关于颗粒级配参数的毛细黏聚力与抗拉强度表达式。需注意：这种描述持水及非饱和强度特性的土壤转换函数适用于以边界减湿持水曲线为基础的颗粒级配分布连续砂土，而增湿曲线取决于减湿曲线的最大基质吸力值，故而未考虑滞回效应，有待进一步深入研究。

2 基于颗粒级配参数预测砂土持水曲线的土壤转换函数

2.1 基于VG模型的典型土壤转换函数 为描述砂土在工程实际应用范围内的持水曲线，一般不考虑残余状态，可引入有效饱和度Se表述。在广泛应用的VG模型中，持水曲线可表示为：

式中：ψ 为基质吸力；Sr和Sres分别为饱和度以及残余饱和度；a 表示与进气值有关的参数；n 表示与持水曲线减湿率（即其直线段斜率）有关的参数。

如研究背景所述，持水曲线可依据土壤转换函数由颗粒级配参数确定。在构建土壤转换函数时，学者们多以VG 模型为基础，采用颗粒级配曲线反映的关键信息预测该模型中的参数a 和n 。Vereecken等［2］采用土粒含量、含碳量以及干密度构建土壤转换函数，虽可覆盖从砂土至黏土的土材料，但对某些砂土的预测精度较差。为此，Schaap 等［23］以砂土为研究对象，通过神经网络分析将a表示为dp的反比例函数，n 表示为np和干密度ρd的函数；随后，Chiu等［24］构建了a 与d50的反比例函数以及n 与的多项式函数。这两种典型土壤转换函数如下所示：

式中：ai和ni均为拟合参数（i=0，1，2，3，…）；dp和np分别为表征平均粒径和粒径不均匀程度的经验参数；σg为颗粒级配曲线的标准差。由式（2）可知，a一般与平均粒径成反比；n可与粒径均匀程度建立关系，原因在于减湿过程主要由孔径分布控制，而孔径分布与颗粒级配曲线存在固有关系［28］。由此可见，为便于工程实际应用，以参数a 和n 为研究对象，如何采用颗粒级配曲线的关键参数更为简便地预测砂土持水曲线值得深入研究。

2.2 基于量纲分析法描述颗粒级配参数与持水曲线的关系 依据文献［29-31］，控制粒径d60、有效粒径d10、d30、不均匀系数Cu和曲率系数Cc这5个典型颗粒级配参数可用于预测土的渗透系数函数与持水曲线。由于d60在计算Cu和Cc时出现，故采用该粒径代替d50描述砂土的平均粒径可简化下文的预测过程。因此，利用d60、Cu和Cc这3个颗粒级配参数控制砂土颗粒级配曲线的形状。

式中：ψ∗和a∗均考虑了d60的影响；参数n 的含义同式（1）。通过分析式（5）中的量纲，并结合式（2）所示的典型土壤转换函数可知：参数n 可表示为Cu的函数，而无量纲参数a∗与Cu有关，或为常数，故Se可近似认为仅与ψ∗和Cu有关。

为在参数n 与Cu的关系中考虑砂土这种典型颗粒材料的基本物理特征，采用两种颗粒级配分布极端的理想颗粒材料（颗粒简化为球体颗粒）描述参数n 的极限值，如图1所示：

（1）完全均匀的颗粒材料（Cu=1）：这种材料内的孔隙可视为等径球体颗粒间液桥相互连接形成的等径孔喉（图1（a）），孔径变化范围很小；当基质吸力增至进气值（由该孔喉半径控制），几乎所有孔喉均开始排水［32-33］，此时持水曲线的直线段斜率很陡，故在式（1）中n →∞。

（2）完全分散的颗粒材料（Cu→∞）：这种材料中的所有孔隙均被细颗粒充填，水分很难排出，故持水曲线的直线段斜率很缓（图1（b）），式（1）中n值会减小至1。

需注意：与式（2）所示的已有土壤转换函数不同，下文构建的土壤转换函数（表征参数n）必须满足这两种理想颗粒材料的极限条件。

图1 两种理想条件的颗粒材料持水曲线

2.3 砂土持水曲线的补充试验 在UNSODA数据库中，大多数土的Cu值较高，未能覆盖图1（a）的完全均匀理想条件。为此，在对该数据库中不同砂土的持水曲线进行分析前，选取4种颗粒级配分布较均匀的砂土进行持水曲线的补充试验，其中两种砂土分别取自榆林市毛乌素沙漠以及西安市东郊浐河（下文简称毛乌素砂和浐河砂），分属细砂和中砂；另两种砂土由粒径在0.2-0.4 mm和0.4-0.8 mm范围内的中砂筛分而得（下文简称筛分砂Ⅰ和筛分砂Ⅱ）。这4种砂土的颗粒级配曲线如图2所示。

采用Fredlund和GCTS公司联合研制的GCTS土水特征曲线仪对这4种砂土的饱和试样进行减湿持水试验。试样为圆柱形重塑试样，其高度和直径为3.19×7.10 cm，是由原始扰动砂土经过过滤、加水、搅拌和静置后再利用压样法制成的，初始含水率控制在10%左右，初始干密度控制在1.40 g/cm3左右。试验前需将制成的试样进行抽气饱和，随后擦除其表面附着的影响含水率或饱和度测定值的水膜，再称取饱和试样的质量，以计算饱和试样在试验前的饱和含水率。具体的试验操作步骤和基质吸力平衡标准参见文献［34］。这4 种砂土的持水实测数据以及采用VG 模型的拟合曲线如图3 所示，相应的均方根误差（RMSE）、误差平方和（SSE）与相关系数（R2）分别在0.0258-0.0425、0.0093-0.0278、0.9887-0.9963范围内变化，表明VG模型对这4种砂土的实测数据拟合效果很好；持水曲线的减湿率与图2中颗粒级配曲线的直线段斜率密切相关，而且土样的粒径越不均匀会使其越难排水。

图2 4种砂土的颗粒级配曲线

图3 4种砂土的持水实测数据与相应的VG模型拟合曲线

2.4 基于UNSODA数据库与持水试验结果构建土壤转换函数 对土壤转换函数的构建主要以UNSO⁃DA数据库为基础，该数据库由780个土样的持水曲线及其饱和-非饱和渗透系数实测数据构成。为有效、可靠地分析数据，在选取土样时主要遵循两方面原则：一方面，颗粒级配分布连续，实测粒径最小值小于d10，最大值大于d60，以确定d60和Cu；另一方面，持水曲线实测数据处于边界减湿阶段且在较高基质吸力下达到残余状态（饱和度较低），具体而言，在半对数坐标系内，当3个实测数据点构成的持水曲线在其中基质吸力最高值处的斜率小于0.15且最终饱和度低于0.2，则可假定这组实测数据达到了残余状态。据此从数据库中选取了70个砂土样作为分析对象，这些土样的砂粒含量大于60%且Cu＜100。对这些土样的持水实测数据仍采用VG 模型（式（1））进行拟合，相应的RMSE、SSE、R2分别在0.0126-0.0848、0.0016-0.0856、0.9328-0.9991范围内变化，表明VG模型对这70个砂土样的实测数据拟合效果很好，进而求得参数a 和n（包括补充的4种砂土）；诸如d10、d30、d60等土颗粒级配参数可通过对半对数坐标系内的颗粒级配曲线插值求得。

进一步综合分析UNSODA数据库中70个砂土样以及另外4种砂土样的颗粒级配参数与持水曲线模型参数之间的关系。如2.2节所述，在式（4）中假定Cc与Cu密切相关，因此在对数坐标系内绘制了74 个砂土样Cc与Cu的关系用以验证该假定，如图4（a）所示，Cc与Cu之间可用线性关系较好地描述。颗粒级配曲线的直线段斜率（含割线斜率）在半对数坐标系内可定量简化为：

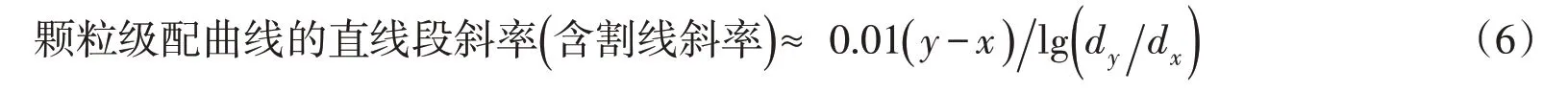
式中：dx和dy分别表示筛余量为x %和y %对应的特征粒径。若采用不均匀系数Cu=d60d10描述，则其斜率为0.5 lg Cu。74个砂土样的参数n 与lg Cu的关系如图4（b）所示，两者的关系满足图1所示的两种极限条件：当Cu趋于1时，参数n 趋于无穷大；当Cu很大时，参数n 趋于1。n 关于lgCu的表达式为：

式中：ξ1为拟合参数（由最小二乘法确定），ξ1≈1.07，拟合精度见图4（b）中的RMSE、SSE、R2。

a 与d60的关系如图4（d）所示（拟合精度见图4（d）中的RMSE、SSE、R2）。需注意：本文假定砂土干密度的变化很小且未考虑颗粒棱角的不规则形状，这都可能成为图4（b）和图4（c）的误差来源。

图4 持水曲线模型参数与颗粒级配参数的关系

2.5 土壤转换函数的验证 式（7）和式（8）的两种土壤转换函数对74个土样参数a 和n 的预测值及实测持水数据对a 和n 的拟合值如图5（e）（f）所示。此外，Schaap等［23］基于神经网络以及Chiu等［24］基于贝叶斯概率原理提出的两种土壤转换函数（式（2））亦可预测这74个土样的参数a 和n，这两种土壤转换函数的预测结果如图5（a）-5（d），可与式（7）和式（8）的预测结果进行对比以评价新型土壤转换函数的有效性。需注意：由于选取的土样与文献［23-24］不尽相同，因此这里采用最小二乘法对74个土样的参数a 和n 进行拟合以确定Schaap等［23］和Chiu等［24］提出的土壤转换函数所需参数，以便进行更为合理的分析和评价。分别采用RMSE、SSE、R2定量评价Schaap等［23］、Chiu等［24］与提出的土壤转换函数预测效果，亦如图5所示，这三种土壤转换函数对参数a 和n 的预测值较持水实测数据对a 和n的拟合值存在一定偏差，这可能是采用VG模型对持水实测数据进行拟合确定参数a 和n 的过程中存在一定误差所致。然而，对比图5（a）（c）（e）可知，式（7）对参数n 的预测效果因其RMSE值和SSE值更小且R2值更大而优于Schaap等［23］、Chiu等［24］提出的土壤转换函数，不仅如此，式（7）还显著改进了对颗粒级配分布均匀砂土的n 值预测效果（见图5中4种砂土的补充试验结果），表明了对均匀颗粒材料进行理论描述的必要性。因此，这种将土基本物理特征与回归分析相结合的土壤转换函数较纯回归分析模型预测效果更好。

对比图5（b）（d）（f）可知，这3种土壤转换函数对参数a 的预测因其RMSE、SSE和R2三者数值相近而效果相当，其中式（8）和Chiu 等［24］提出的转换函数效果略好。由于在计算Cu时需要确定d60，因此式（8）无需再引入参数dp或d50。

图5 参数a和n的预测值（采用土壤转换函数）及其拟合值（基于持水曲线实测数据）

在式（7）中，颗粒级配曲线的直线段斜率影响可通过Cu描述。不仅如此，颗粒级配曲线的割线斜率亦可采用其它特征粒径比描述，并可在式（7）中用这些特征粒径比替换Cu，如表1 所示，将d10、d20和d30作为dx，d60、d70、d80和d90作为dy，进而采用dydx替换Cu，即可得到相应的ξ1、RMSE、SSE 以及R2值。由表1 可知，采用d10作为dx的预测精度高于采用d20和d30；采用Cu（即d60d10）的预测精度最优，尽管d90d10的预测精度最接近Cu，但Cu对土材料更常用、易测。需注意：式（8）采用d60描述平均粒径，并构建了a 与之成反比的土壤转换函数，这与文献［2，22-24］得出的“参数a 与平均粒径成反比”的结论一致，而诸如d90、d80、d70等其它特征粒径的物理意义与平均粒径差异显著，因此未讨论其它特征粒径与参数a 的关系。

表1 采用不同特征粒径比对参数n 的预测精度

不仅如此，还利用已有文献［35-37］中6种砂土的持水实测数据验证提出的土壤转换函数对74个砂土样数据库以外持水曲线预测的有效性。这6种砂土的颗粒级配曲线如图6（a）所示，其平均粒径和均匀程度不同。由图6（a）可知，文献［35］中350号细砂和壤质砂土的d60值相近但Cu值差异显著。先由式（7）和式（8）预测参数n 和a ，进而将其代入式（1）得到持水曲线，这两种砂土样从完全饱和状态开始的边界减湿持水实测数据及其相应的预测曲线如图6（b）所示（拟合精度见图6（b）中的RMSE、SSE、R2），350号细砂的Cu值相对较小，而预测曲线与实测数据较为吻合；壤质砂土的预测曲线在较高基质吸力范围内较实测数据存在误差，原因在于残余饱和度取值存在不确定性。

图6 采用新型土壤转换函数对已有文献中6种砂土持水实测数据的预测结果

此外，对比文献［36-37］中4种砂土样从完全饱和状态开始的边界减湿持水实测数据及其相应的预测曲线（如图6（c）（d））可得到与图6（b）类似的结果，相应的拟合精度亦如图6（c）（d）中的RMSE、SSE、R2所示，提出的土壤转换函数对这4种砂土持水曲线的预测效果总体较好，仅黏质砂土和Chiba砂土在较低基质吸力范围内预测效果相对较差，分析其原因：当土样的d10很低时，其残余状态很难确定；新型土壤转换函数未考虑土样干密度和土结构的影响，当黏粒含量较高时对进气值的预测会存在误差。然而，式（7）和式（8）所示的新型土壤转换函数通过颗粒级配参数d60和Cu即可快速实现对不同种砂土持水曲线较为合理的预测。

3 基于土壤转换函数描述颗粒级配分布对砂土非饱和强度特性的影响

3.1 颗粒级配分布对非饱和砂土毛细黏聚力的影响 砂土的非饱和强度特性一般通过颗粒骨架传递的有效应力来描述。Lu等［27］采用有效饱和度Se描述有效应力参数χ ，进而将有效应力公式代入莫尔-库伦强度准则可得到非饱和抗剪强度τf的表达式：

式中：φ′为有效内摩擦角；c′为有效黏聚力。砂土颗粒间诸如范德华力和黏结作用等黏聚效应很小，故c′可忽略不计，而剩余部分ccap=Seψtanφ′称为毛细黏聚力，反映了水分含量对强度的贡献。如研究背景所述，砂土的非饱和强度特性与其持水特性密切相关。若采用VG模型描述基质吸力与有效饱和度的关系，则可直接将土壤转换函数代入非饱和抗剪强度表达式中。具体而言，先把式（1）表示的持水曲线代入式（9）（c′=0），则非饱和抗剪强度τf可表示为基质吸力ψ（或有效饱和度Se）的函数：

式中：参数ξ1和ξ2分别近似取为1.07和12.07（如2.4节的统计分析所述）；σw取0.073 N/m（如2.2节所述）。

对非饱和砂土进行直剪试验或三轴试验时测得的毛细黏聚力亦可采用颗粒级配参数预测。众所周知，粗颗粒之间的范德华力和双电层作用可忽略不计，故非饱和砂土中的黏聚力主要由水分的毛细作用产生。依据式（9）（c′=0）和式（10），毛细黏聚力ccap关于ψ 或Se可表示为：

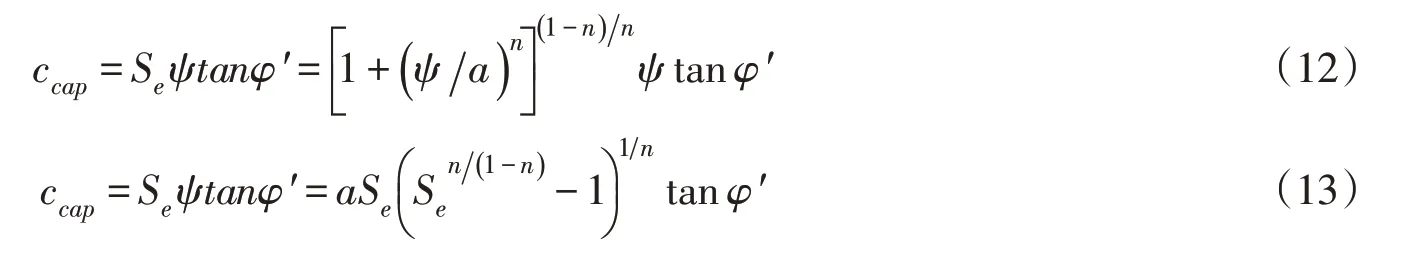
若考虑颗粒级配参数与有效饱和度或基质吸力的影响，则由式（11）可将ccap关于ψ 或Se表示为：

图7 采用d60 和Cu 预测文献［38-40］中三种砂土的持水曲线与毛细黏聚力

由式（15）可知，当有效饱和度一定时，毛细黏聚力ccap与颗粒级配参数d60成反比。利用已有文献［38-40］中对不同颗粒级配分布的砂土进行控制基质吸力的直剪试验或三轴试验结果，整理持水及毛细黏聚力的实测数据与土壤转换函数的预测曲线（图7）。由图7（a）中的RMSE、SSE、R2可知，新型土壤转换函数预测的持水曲线与其实测值总体较为吻合，仅对花岗土的持水试验结果预测偏小。分析其原因：花岗土（d60=0.11 mm且Cu=90）因其颗粒级配分布很不均匀而在持水试验中很难排水，故土壤转换函数对减湿率的估算存在误差。

关于毛细黏聚力随基质吸力的变化规律，Hossain等［38］以花岗土为研究对象，其有效内摩擦角约为38°，沿减湿路径在一定基质吸力和法向应力下对试样进行剪切试验。毛细黏聚力可由莫尔-库伦强度包线计算得到，相应的试验结果在远离进气值的较高基质吸力范围内测得，如图7（b）所示，花岗土的毛细黏聚力随基质吸力呈单调递增趋势，式（14）的预测曲线与实测数据趋势较为吻合。Gallage等［39］以Edosaki砂土（d60=0.27 mm且Cu=17）为研究对象，其有效内摩擦角约为46.2°，对比分析减湿路径下不同基质吸力对应的毛细黏聚力，亦如图7（b）所示，式（14）对其毛细黏聚力的变化趋势较为吻合。由于Edosaki砂土较花岗土平均粒径更大、颗粒级配分布更均匀，故其毛细黏聚力低于花岗土。Likos等［40］以砂质崩积土（d60=0.26 mm且Cu=1.9）为研究对象，进行了低基质吸力和低应力条件下的直剪试验。这种材料较Edosaki砂土的平均粒径相近，但颗粒级配分布更均匀，有效内摩擦角约为38.8°，选取法向应力最低时的不同基质吸力对应的毛细黏聚力进行对比分析，亦如图7（b）所示，毛细黏聚力随基质吸力增高呈先增后减趋势，并存在峰值；式（14）的预测曲线不仅与实测数据趋势较为吻合，而且可反映毛细黏聚力的峰值。

对式（13）关于Se求导，并令该导数为零，可求得毛细黏聚力峰值对应的有效饱和度特征值S∗e：

不仅如此，还从理论计算上分析了d60和Cu对ccap的影响。基于d60和Cu计算的持水曲线和毛细黏聚力理论值如图8所示（假定有效内摩擦角取35°）。先令d60=0.2 mm，而Cu取2、10、50，分别对应从细砂至粉质或黏质砂土的砂土材料，进而采用土壤转换函数（式（7）和式（8））和式（15）算得持水曲线以及ccap随Se的变化曲线（如图8（a）（c）），结果表明：当d60相同时，Se=0对应的ψ 随Cu增大而骤增；Se＜0.2范围内的ccap亦随之骤增；对含有一定量粉粒或黏粒的土材料（Cu＞11），其ccap不存在峰值，而且当Se较低时，ccap非常高。此外，由图8（b）（d）可知：当Cu相同时，持水曲线随d60增大而左移，原因在于进气值随d60增大而减小；ccap(max)随d60增大呈减小趋势。

3.2 颗粒级配分布对非饱和砂土抗拉强度的影响 依据文献［27］中抗拉强度与吸应力的关系，采用莫尔-库伦强度准则，可推得非饱和砂土的单轴抗拉强度σt与基质吸力ψ 的关系为（σt=-σ1且σ3=0）：

式中：σs为吸应力。若考虑颗粒级配曲线与持水曲线之间的关系，则抗拉强度可表示为：

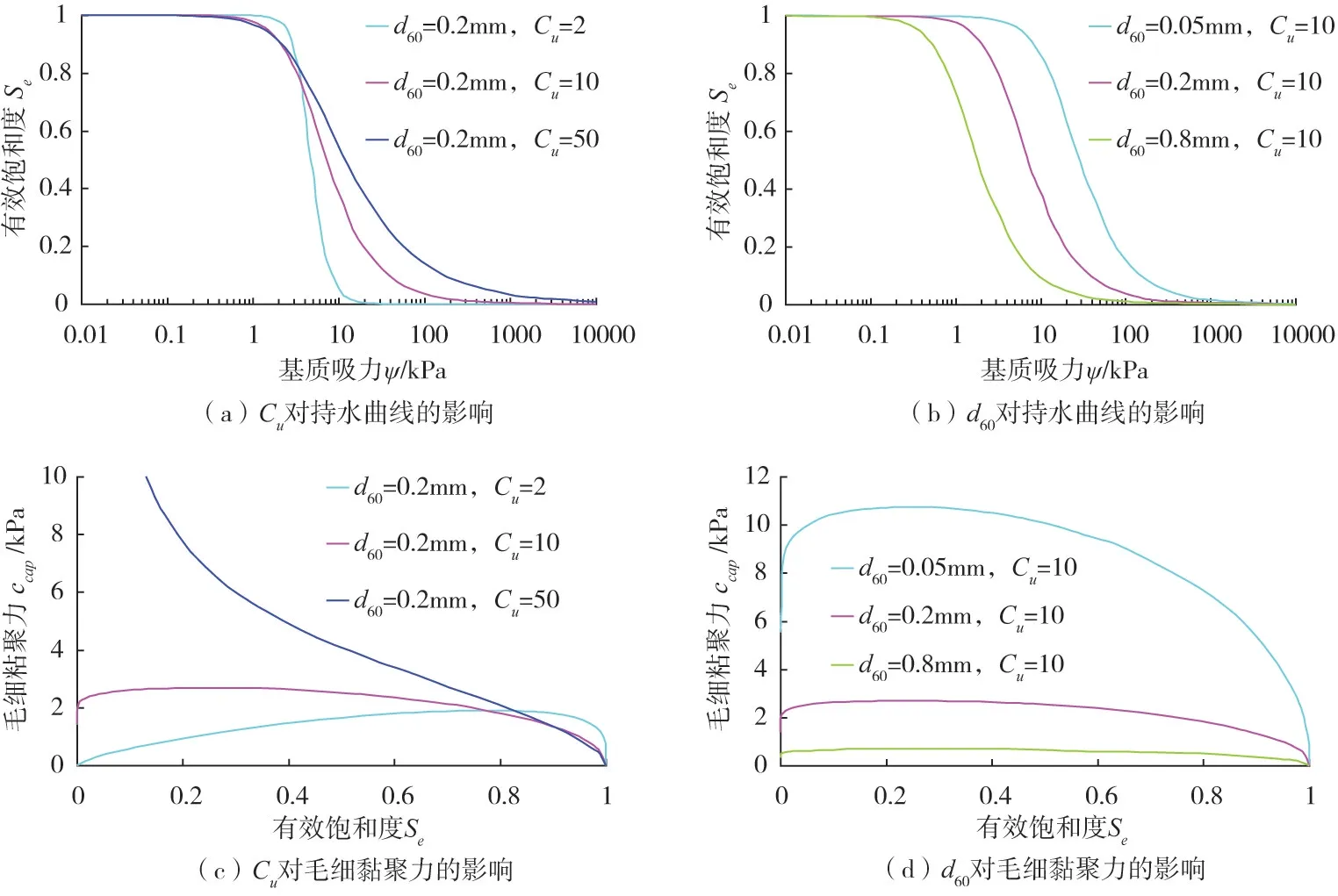
图8 颗粒级配参数对持水曲线和毛细黏聚力的影响

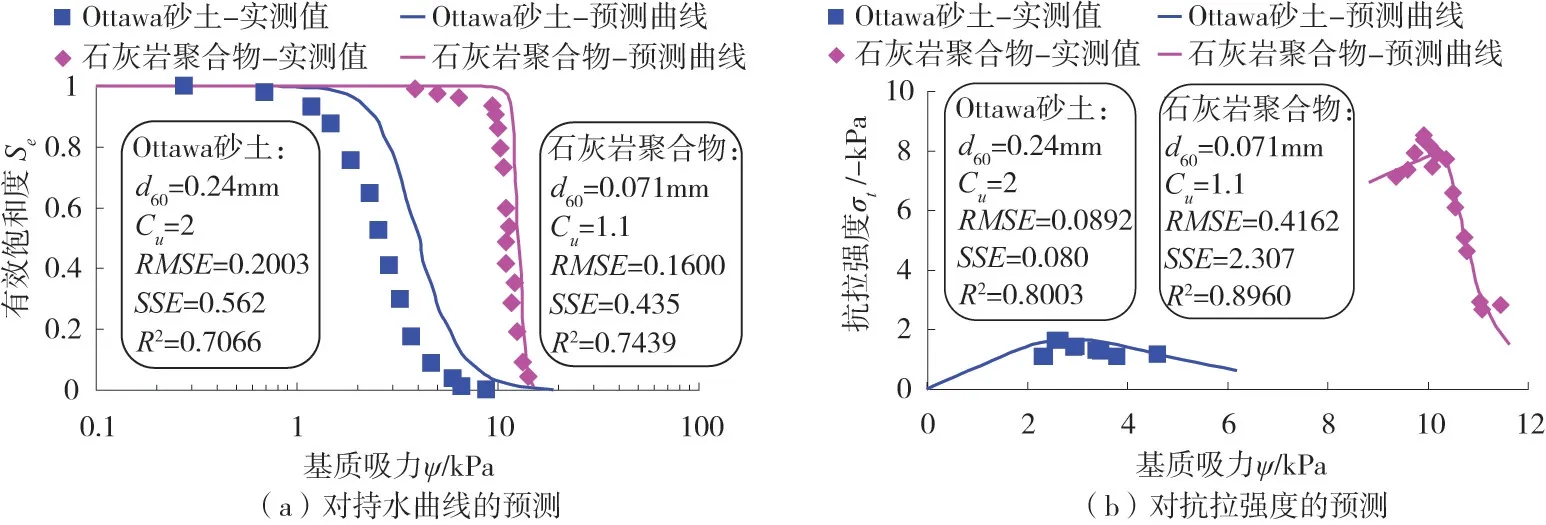
图9 采用d60 和Cu 预测文献［41-42］中两种砂土的持水曲线和抗拉强度

Lu等［27］采用文献［41-42］中石灰岩聚合物和Ottawa砂土的抗拉强度试验结果验证了他们提出的有效应力表达式。这里同样采用文献［41-42］的实测数据验证基于颗粒级配参数对这两种材料抗拉强度的预测效果。石灰岩聚合物的颗粒级配分布非常均匀，其平均粒径为0.071 mm，故d60≈0.071 mm且Cu≈1.1；Ottawa 砂土的d60=0.24 mm 且Cu=2。依据式（7）和式（8）即可预测这两种砂土的持水曲线，持水实测数据及对应的预测曲线如图9（a）所示（预测精度见图9（a）中的RMSE、SSE、R2），土壤转换函数对石灰岩聚合物持水曲线的预测效果相对Ottawa 砂土更好，对Ottawa 砂土的预测误差可能源于对其进气值的估算误差。

Baltodano-Goulding［43］测得Ottawa砂土的有效内摩擦角为36°，而石灰岩聚合物这种细粒材料的有效内摩擦角可近似为40°。将颗粒级配参数和有效内摩擦角代入式（20），可计算并绘制出这两种砂土抗拉强度关于基质吸力的预测曲线，与其对应的抗拉强度实测值进行对比分析（如图9（b）），由预测精度（RMSE、SSE、R2）可知：预测曲线的变化趋势与实测数据较为吻合。对抗拉强度的预测误差可能源于有效内摩擦角的测量误差。

4 结论

基于颗粒级配参数（控制粒径d60和不均匀系数Cu）提出了预测非饱和砂土持水曲线的土壤转换函数，在其中分别考虑了完全均匀和完全分散的两种理想条件。对74个砂土样（其中70个来源于UN⁃SODA数据库，另外4种砂土样为补充试验对象）的van Genuchten 持水曲线模型参数进行量纲分析和回归分析，提出了用d60和Cu表示的土壤转换函数预测该模型参数。此外，将提出的土壤转换函数代入非饱和强度表达式，构建了砂土的非饱和强度与颗粒级配参数之间的关系。主要得出以下结论：

（1）基于量纲分析法构建了考虑了砂土基本物理特征的土壤转换函数，即参数a（与进气值有关）和n（与持水曲线减湿率有关）分别与d60和lgCu成反比，用于表征持水曲线与颗粒级配曲线之间的关系。采用均方根误差（RMSE）、误差平方和（SSE）与相关系数（R2）对比分析不同土壤转换函数对砂土样持水实测数据预测结果表明：新型土壤转换函数对持水曲线模型参数的预测效果优于已有土壤转换函数。

（2）通过分析经典非饱和强度理论的物理特征可知，水分产生的非饱和强度不仅与持水特性有关，而且与土颗粒级配曲线存在本质联系，从而针对砂土推得关于d60和Cu的非饱和强度表达式。

（3）采用已有文献的非饱和强度试验结果验证了这种考虑颗粒级配参数的强度表达式在预测非饱和砂土毛细黏聚力与抗拉强度时的有效性，进而通过颗粒级配参数的影响分析发现：毛细黏聚效应在控制粒径更小或颗粒级配分布更不均匀的砂土材料中更为显著。

本文构建的土壤转换函数以及非饱和强度表达式的优势在于参数易测，当砂土干密度变化很小时，可应用于快速确定砂粒含量大于60%且Cu＜100 的砂土材料参数。对干密度变化显著的土材料（如黏土）如何构建土壤转换函数，则有待进一步研究。