计算研究改性WS2/GQDs异质结构的电学和光催化性能
朱燃燃,李 宁,晋民杰,范 英
(1.太原科技大学交通与物流学院,太原 030024;2.中北大学能源与动力学院,太原 030051)
作为一种低成本绿色材料,碳点 (CDs)在光致发光、光稳定性、生物相容性和无毒性等方面的优异性能使其在太阳能转换、荧光成像和传感等领域有着巨大的应用潜力[1-6]。然而,由于CDs具有较高的电荷复合几率和较强的紫外吸收能力,在光生电荷转移和可见光吸收方面存在挑战。基于碳点建立异质结构或者复合体系能够促进碳点的光生电荷转移和捕获更多可见光。例如,碳点结合不同的化合物(包括贵金属(Ag,Au,Pt)、TiO2、Ag3PO4、ZnFeO4、Fe2O3、C3N4、Ni3S2、Bi2WO6、BiOCl、Cu2O、Cu1.8S和过渡金属硫化物(transition metal dichalcogenides, TMDs))[7 -13])而形成的复合结构具有较好的可见光吸收和电荷转移效率。碳点可以成为电子受体和供体,但如何在异质结构中更好的设计与利用碳点仍是目前需要解决的问题。
在这些碳点基复合体系中,二维(two dimensional,2D)TMDs具有比表面积大、可见光吸收强、边缘活性位多、光生载流子迁移距离短的优点[14]。2D TMDs结合CDs形成的复合结构能够提高光催化活性。例如, Atkin等研究表明CDs/2D WS2的杂化结构提高对刚果红(CR)染料光催化降解效率。Fang等人证明了光激发电子从碳点到MoS2单层膜的有效转移。然而,二维MoS2或WS2的边缘位点具有催化活性,而基平面是化学惰性的[15-20],这限制了太阳能的高效转化与利用。研究表明通过二维TMDs的基平面掺杂改性能够改善化学惰性。例如,氧掺杂可能提供更多的缺陷导致更多催化活性位点。惰性基面可以通过氮、氟共掺杂的协同作用被激活。因此,利用改性的二维TMDs负载碳点来构建异质结构,研究其界面相互作用对设计高性能光催化剂具有重要意义。
基于密度泛函理论(DFT)的计算成为研究纳米材料内在特性的有效方法,为其潜在的应用提供理论支持。因此,本文选择碳点的一种—石墨烯量子点(GQDs)[21],与未掺杂和O改性的单层WS2(WS2和O-WS2)形成范德华异质结构,通过半经验色散校正(D)加入标准kohn-sham-DFT形成DFT-D方法[22-25]来描述二维材料的范德华相互作用。然后用DFT-D方法研究了异质结构的结构、电子和光催化性能。
1 计算方法


表1 不同元素的C6 参数 (Jnm6 mol-1) 和范德华半径()
2 结果与讨论
首先,为了消除悬挂键的影响[27],假设GQDs的所有边缘碳原子都被H原子完全钝化,以此构建锯齿形边缘的C24H12结构(图1 (a)).如图1 (b)所示,构建包含147个原子的7×7×1 超胞,并直接用O替换S原子实现O改性WS2.几何优化以后,二硫化钨单层的晶格常数a=b=3.153和α=β=90°,γ= 120°,结构优化结果与已发表的数据保持一致[28]。O-WS2的形成能(Ef)可由文献提供的公式计算[29]。O-WS2的Ef值为负,说明O掺杂更容易取代S原子,这些掺杂体系相对稳定。接着构建Total-WS2(T-WS2/GQDs(包含WS2/GQDs及O-WS2/GQDs))异质结构,如图1(c)-(d)所示。单层T-WS2与GQDs的距离为h(hpreset为默认设置值,hAO为优化值)。为了准确研究上述异质结构的电子和光催化性能,需要找到最稳定T-WS2/GQDs界面。异质结构稳定性的判据为界面结合能。根据文献,T-WS2/GQDs界面的结合能(Eb)计算公式为[29,30]:
Eb=ET-WS2/GQDs-EWS2-EGQDs-(μD-μS)
(1)
其中ET-WS2/GQDs,EWS2andEGQDs是T-WS2/GQDs异质结构、单层WS2及GQDs的总能量,μSandμD是被取代原子S和掺杂原子O的化学势。

图1 原子构型图Fig.1 Atomic configurations of GQDs

图3(a)-(d)为单层WS2、O-WS2、WS2/GQDs和O-WS2/GQDs的分态密度图,嵌入图分别为四种样品的能级结构。从图3(a)可以看出,价带和导带主要由W 5d和S 3p轨道杂化构成。价带顶(VBM)和导带底(CBM)都位于布里渊区K点上,说明WS2为直接带隙半导体、单层WS2的带隙值为1.931 eV,这值与C.Y.Wang等[30-31]利用GGA计算获得的单层WS2带隙(1.91 eV)接近。A.L.Elías等[32]通过硫粉硫化WOx/SiO2制备单层WS2,利用PL谱测得带隙值在2.0 eV附近。通过对比发现,本文计算得到的单层WS2直接带隙低于实验得到的直接带隙,这是由于第一性原理计算本身低估禁带宽度的缘故。当单层WS2掺入O之后,如图3 (b)所示,VBM和CBM仍在K点处,并且它们主要来源于W 5d、S 3p 和O 2p的轨道杂化。

图2 (a) 最优hpreset 和hAO下的形成能及结合能;(b)石墨烯量子点的能带结构和分态密度图(嵌入图)Fig.2 (a)The formation energy and the binding energy at the optimal hpreset or hAO; (b)the band structure and partial density of states (PDOS,the inset figures) of GQDs
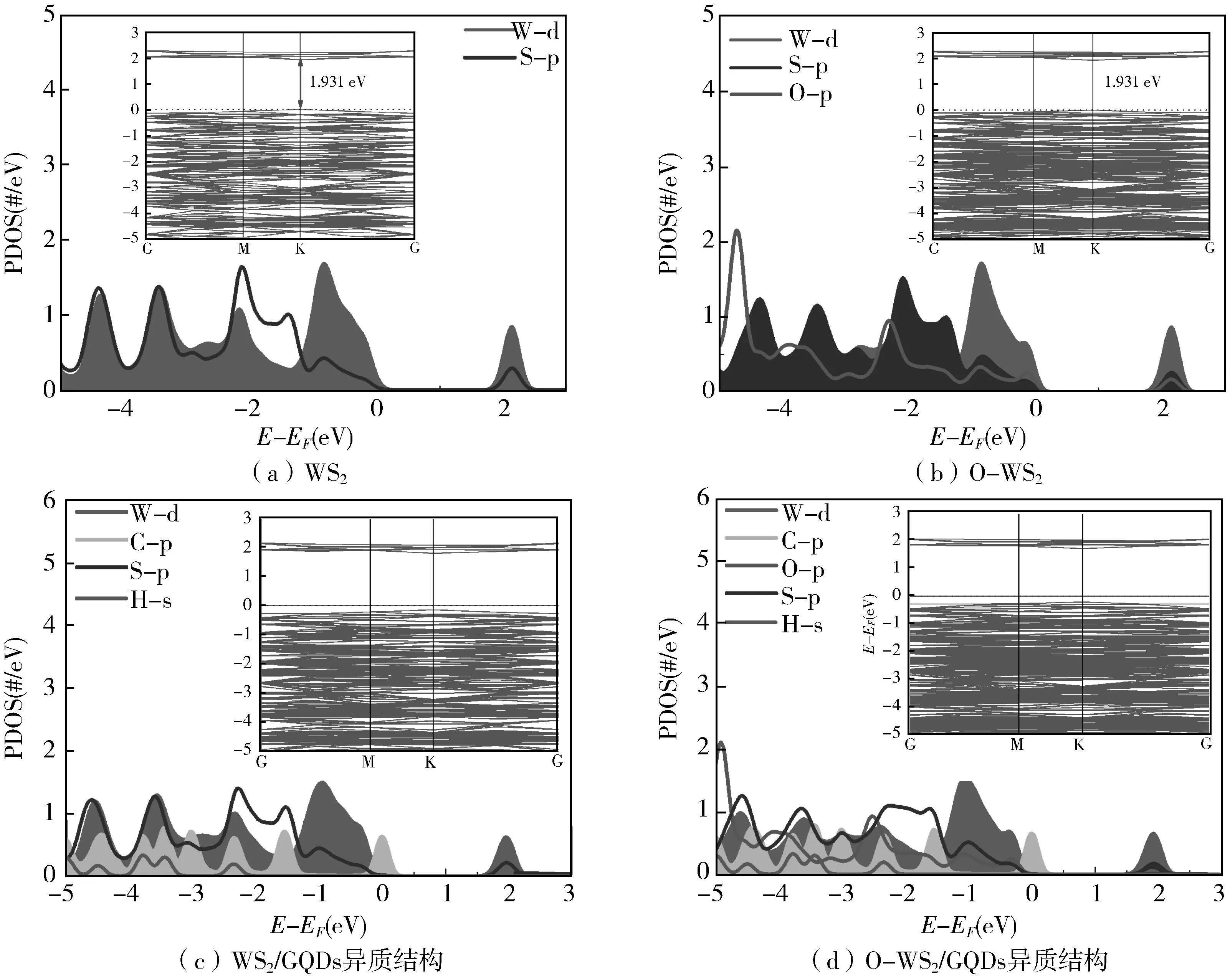
图3 分态密度和能带结构(嵌入图)Fig.3 Partial density of states (PDOS) and band structure (the inset figures)
当WS2、O-WS2与GQDs形成异质结构后,如图3 (c)-(d) 所示,在费米能级的下方出现了能级,主要是由 C2p轨道贡献。WS2/GQDs和O-WS2/GQDs异质结构的价带顶和导带底的能量位置分别为-0.16 eV,-0.21 eV和1.78 eV,1.72 eV.最高占据轨道和最低未占据轨道间的能隙大小EgHL分别为1.78 eV和1.72 eV。同时,当O掺杂WS2负载GQDs后,价带及导带边缘处W 5d、S 3p 和O 2p的轨道杂化可以产生较强的波函数重叠,有利于光生电子从GQDs注入到O-WS2上。
为了提高光催化活性,增加太阳光吸收非常必要。本文利用介电函数计算得到吸收光谱[32-37]:
(2)
其中ω是光频率,ε2(ω)和ε1(ω) 是介电函数的虚部和实部。ε1(ω) 由公式对电子态的求和决定,ε2(ω) 利用 Kramers-Kronig关系获得,如下所示:
(3)
〈μck+eαq|μνk〉〈μνk+eβq|μνk〉
(4)
如图4所示,GQDs的吸收峰主要在紫外光波段(>~3.10 eV),并且吸收峰强度相对较低,这不利于吸收较多的太阳光,从而产生较少的光生电荷。而单层WS2在~1.50 eV~6.50 eV 之间有较强的吸收,并且在~3.20 eV (A峰)and ~6.60 eV(B峰)附近的吸收峰主要来自于W 5d和S 3p轨道之间的跃迁。 在构建T-WS2/GQDs异质结构后,相比于GQDs,吸收峰明显红移并且强度明显增加,显著提高了在可见光区域的吸收能力。
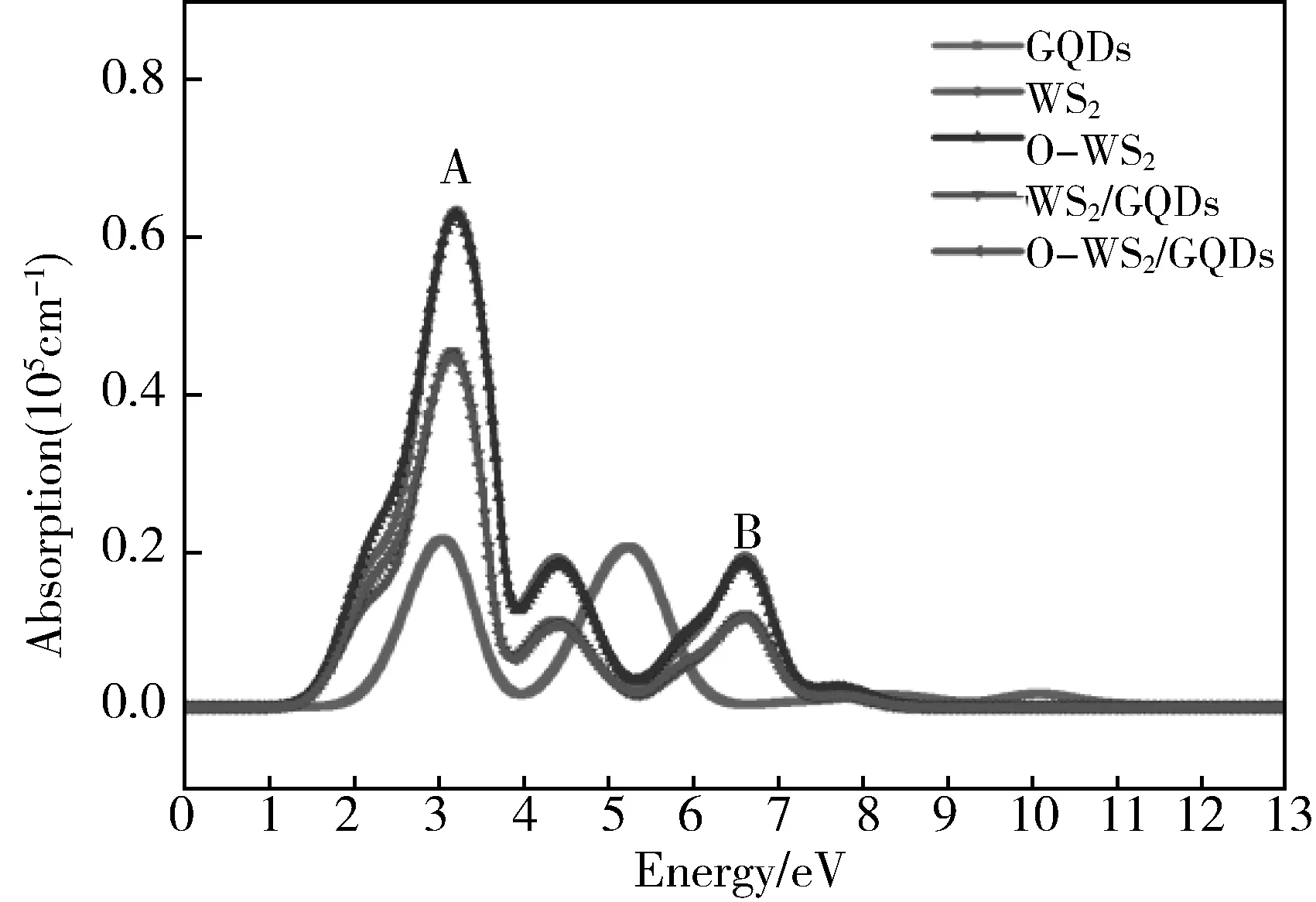
图4 光学性能图Fig.4 Optical absorption

图5 VBM、CBM和其他能级位置Fig.5 The calculated VBM,CBM and other level positions
从上述分析来看,通过构建T-WS2/GQDs异质结构已经得到了合适的能隙和较强的可见光吸收。从另一方面讲,合适的带边位置对于提高光催化活性具有作用。接下来通过价带顶和导带底相比于真空能级的位置来研究氧化还原能力。这些带边位置通过下列公式表示[38]:
EVB=φ=V(∞)-EF
(5)
ECB=EVB-Eg
(6)
其中V(∞),EF,Eg分别为在真空区中的静电势,表费米能级和带隙值。如图5所示,GQDs的 LUMO、HOMO位置 比T-WS2的CBM 、VBM 的位置高,这会形成典型的type-II能级结构,有利于光生电荷的分离和转移。结合态密度和能带结构的分析,在入射光子能量的作用下,C2p轨道上的光生电子能够最终转移到S3p、O2p (仅对于O-WS2/GQDs异质结构)和W 5d的杂化轨道上。O掺杂能激活二维WS2的基平面,产生活性位点。同时, O-WS2/GQDs的氧化还原电位向上移动(图5),说明O掺杂在一定程度上改变了电子结构,使之有利于光催化反应。
3 结论
本文系统研究了石墨烯量子点、纯WS2和O改性WS2、T-WS2/GQDs 异质结构的结构、电学和光催化性能。
(1)O掺杂后负的形成能和O-WS2/GQDs 异质结构更负的结合能说明O更容易取代S原子,并且取代后形成的结构模型比较稳定。
(2)来源于C 2p轨道的能级正好位于T-WS2/GQDs 异质结构的费米能级的下方。相比于GQDs,异质结构的吸收峰红移,吸收强度也显著增加,同时形成了典型的type-II 能带结构,这有利于捕获更多的太阳光和促进光生电荷的分离和转移。
(3)O掺杂可以改变O-WS2/GQDs的电子结构,使之有利于光催化,形成高效的光催化体系。

