双负载无线充电系统交叉耦合分析
鲁丽航,宋卫平,宁爱平,郭 楠
(太原科技大学 电子信息工程学院,太原 030024)
继无线通讯、无线网络之后,无线充电是第三次无线革命[1]。2007年,麻省理工团队的研究小组,利用电磁谐振原理(MRC)成功点亮了2米以外的灯泡[2],目前无线充电设备充电普遍使用这种磁耦合谐振式(MRC)的方法[3]。无线充电技术发展初期国内外做了详细的研究,可优化了电路中的高频逆变电路拓扑结构[4-5]、增加频率锁相跟踪电路为辅助电路[6]、利用超导材料并改变线圈参数和形状[7]等方法分析了功率及效率与工作频率、传输距离、等效负载之间的关系[8],优化了传输功率、效率及传输距离,但近场区的能量没有完全利用,同时还增加了系统的复杂性,提高了成本。
磁耦合谐振充电方式具有一定水平自由度,可完成对多个人工智能终端的充电[9-10],充分利用没有完全利用的能量,达到提升系统效率的目的。但在一对多的充电系统中不仅存在发射端与接收端之间的耦合,还存在负载与负载之间的交叉耦合,这种交叉耦合现象会使得整个系统的分析和设计偏于复杂。文献[11]分析了一对多充电方法的传输过程,但忽略了各个线圈之间交叉耦合对整个系统所带来的影响;文献[12-13]分别分析了一种双负载无线充电系统中的交叉耦合,但文献[13]分析时,第二个线圈为中继线圈,不加任何负载。
本文从双负载系统出发,量化了交叉耦合对多目标无线充电系统的具体影响,并根据传统的补偿网络,从功率的角度分析选择了其中一种补偿网络进行阻抗匹配,最后验证了这种方法的可行性。
1 模型分析
根据接收线圈的排列方式可以分为子母式和接力式,利用该系统对多线圈系统进行推导,图1为三线圈系统的等效电路图,R1、R2、R3为电源等效内阻及各接收线圈的电阻,RL1、RL2是接收电路中的负载电阻;M12、M13、M23为两个线圈之间的互感;L1、L2、L3和C1、C2、C3为发射端和接收端的电感和电容,式(1)为两个线圈之间的耦合系数。
(1)

图1 双负载系统电路图Fig.1 Dual-receiver system circuit
1.1 交叉耦合对电流向量的影响
根据基尔霍夫定律,无线充电系统电路可用式(2)表示。
V=ZI
(2)
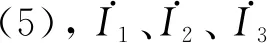
(3)
(4)
(5)
当系统谐振时,整个多目标无线充电
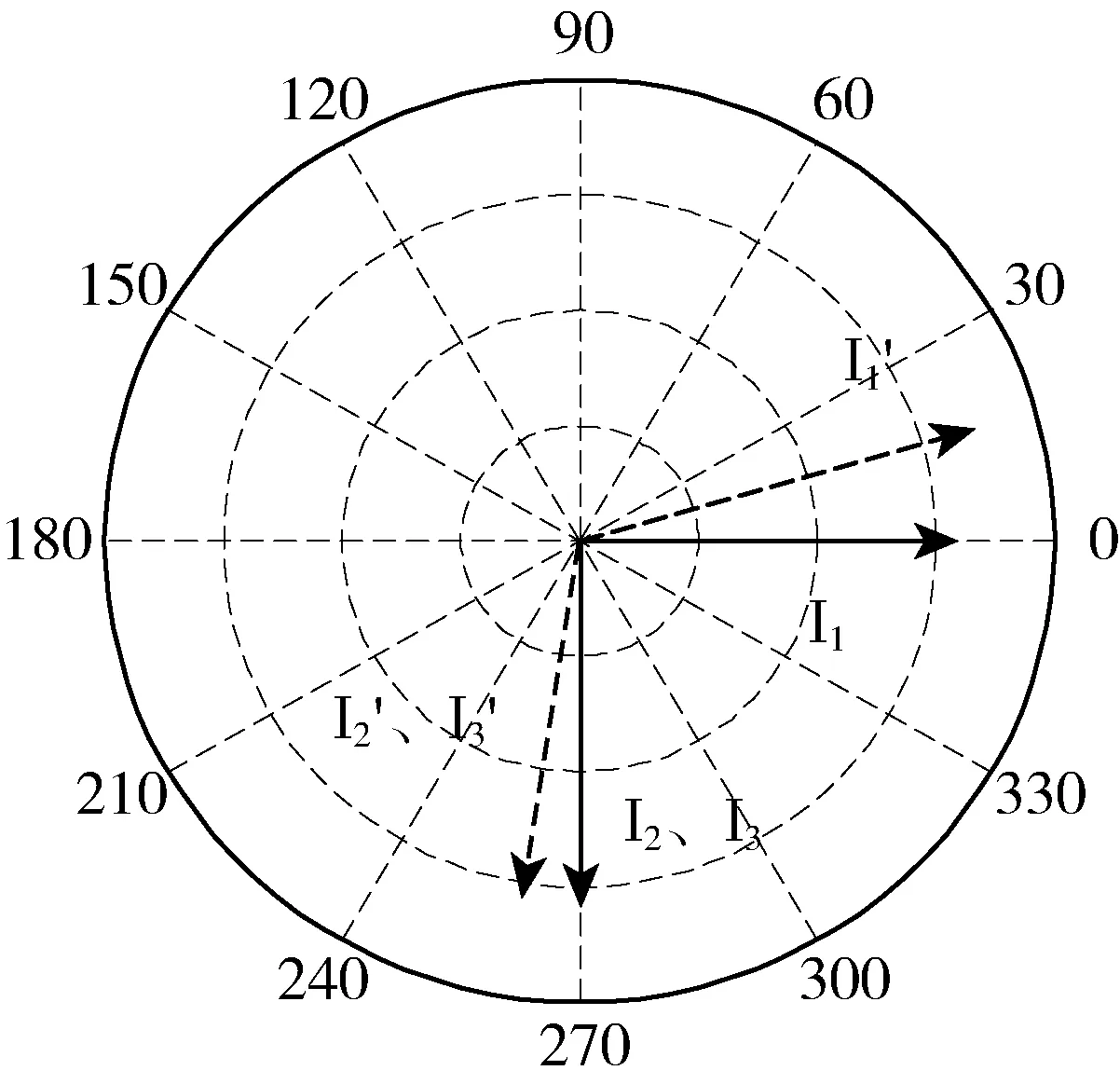
图2 双负载系统电流向量Fig.2 Current vector of dual-receiver system
1.2 交叉耦合对负载端电压和效率的影响
根据图1所设定的参数,可计算出电路中的失谐因子为ξ=Q(ω/ω0-ω0/ω)与耦合因子为u=ωM/R,可反应出交叉耦合使负载电压及效率发生的偏移情况和对系统的影响,更有利于分析谐振点偏移的情况。假设发射端与各接收端的耦合因子相同,将式(1)-(5)联列后进行归一化处理,将三阶代数方程简化为二阶,式(6)为变化后的向量方程,式(7)为求得的归一化电压比表达式,式(8)为系统效率表达式。
(6)
(7)
(8)
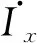
图3(a)为单负载系统归一化电压曲线图,(1,0,0.5)为谐振点,系统处于临界谐振状态,当耦合因子u大于1时,电压发生频率分裂现象;图3(b)为双负载系统归一化电压曲线图,双负载系统在谐振点(1,0,0.5)已经发生了频率分裂,说明双负载系统中存在的交叉耦合使得临界耦合因子变小,谐振点发生了偏移,提前出现了频率分裂现象。
取合因子u=1,得纵向切面图,继续增加n的值,可得到负载个数与负载端电压关系,如图4(a)所示,在ξ=0,ut=0.7时为系统临界谐振点,可计算出发射线圈与接收线圈之间的耦合系数为k=0.147,交叉耦合受线圈间的距离影响,接收端线圈距离越近则交叉耦合越大取不同的ux,分析对双负载系统的影响,如图4(b)所示。
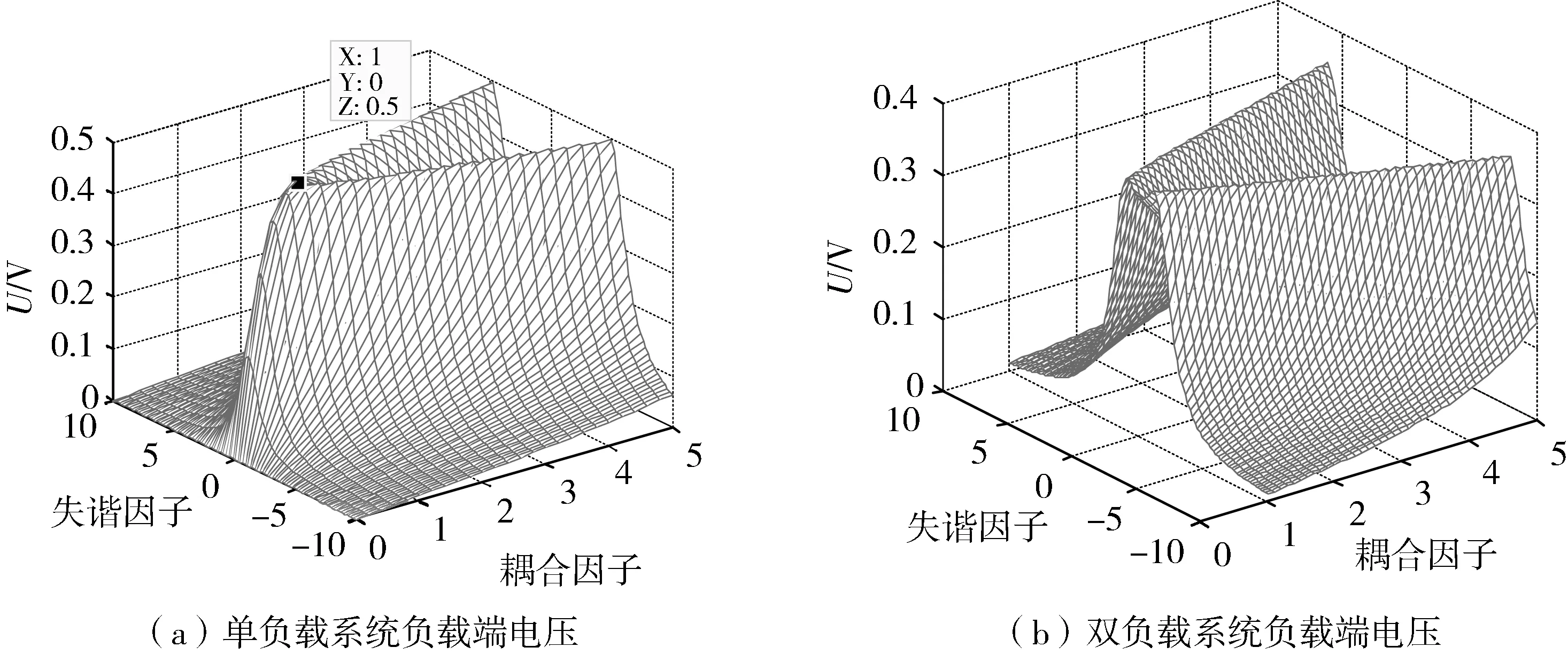
图3 负载端电压三维图 Fig.3 3D diagram of load voltage
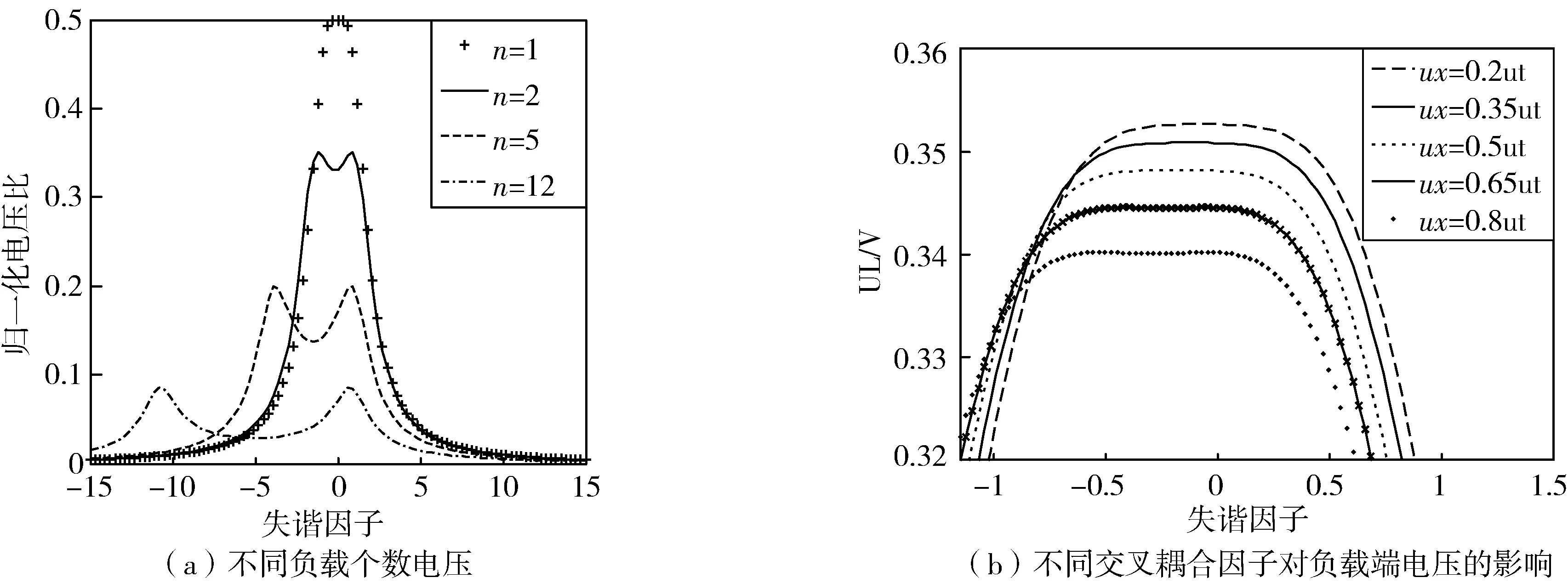
图4 交叉耦合对系统负载端电压影响Fig.4 The effect of cross-coupling on system load voltage
由图4(a)可知,当负载个数增加时,较单负载来说,各负载端电压减小,且与负载个数成反比,同时,谐振点偏移程度越大,频率分裂现象越明显;在4(b)中,根据图形得到对应的数据,当交叉耦合系数取到0.65ut和0.8ut时,谐振点负载端电压不是最高,在两侧出现了峰值,发生了频率分裂现象,0.65ut处的两峰值为0.344 6,谐振点值为0.344 3,0.8ut处的两峰值为0.340 2,点值为0.339 8,且0.8ut比0.65ut两峰值距离大。可见,交叉耦合因子越大,电压越小,对双负载系统的影响也越大,谐振点偏移越明显,当交叉耦合增大到一定程度时,会出现频率分裂现象。
将式(6)与式(8)联列,可得到系统效率,表1为不同交叉耦合下系统的效率表,表中的数据说明由于交叉耦合的存在,阻碍了发射线圈与接收线圈之间的能量传递,系统效率与其成反比,交叉耦合越大,系统效率降低。
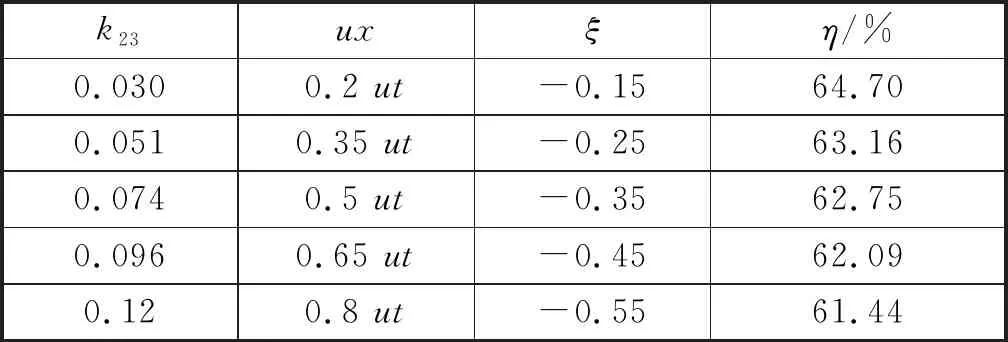
表1 不同交叉耦合下系统效率表
2 系统校正
大多数研究中为了避免交叉耦合带来的影响,在各个线圈中串并联阻抗进行补偿,使得传输功率最大值始终保持在谐振点,实际上,为了得到最大功率值可以将传输功率看成一个函数,将负载的功率问题转换为数学问题,求取最大值点直接得到最大传输功率,再加入匹配阻抗调节补偿系数,常见的补偿网络有串联与并联型,设补偿元件为Z′.
求取发射端最大功率时,采用串联补偿网络将接收端视为谐振状态,在用数学模型确定负载端的补偿网络形式,从接收线圈向发射线圈看,可将接收端电阻等效到发射端,负载间存在的交叉耦合表现为等效电阻的减小,用x表示,如式(9)所示,发射接收线圈间的传输功率表达式为式(10).
x|Z+ZL1|
(9)
(10)
当等效阻抗减小,在电压源或电流源的作用下,回路电流I变大,始终保持传输功率不变,定义电路中的总阻抗为ZC,定义补偿系数r=(Z'+ZL1)/ZL1,用补偿系数来表示补偿元件大小,当x发生变化时,通过调节r来使得传输功率保持在最大值,不同补偿网络下的传输功率表达式(11)、式(12).
(11)
(12)
式(12)为并联补偿系统功率传输公式,对于并联式补偿网络来说,当补偿系数x发生改变时,Z'发生变化,也使得传输功率发生变化,而式(11)表示的串联补偿功率传输公式中,功率的变化只与补偿系数x有关,故选取串联式补偿,系统补偿为SSS型,同时,在式(11)中,当x/(r2+x2)取最大值时,传输功率最大,定义传输因式P(x).
P(x)=x/(r2+x2)
(13)
绘制不同补偿系数r值下的传输因式P(x)的图像,图形见图5.

图5 传输因式P(x)模型Fig.5 Transmission factor model
在图5中,传输因式P(x)的极值由补偿系数r决定,当r=x时,整个系统有最大传输功率,r的值越大说明系统交叉耦合情况越严重,传输因式的极值越小,传输功率越小,说明系统由于交叉耦合的影响,整个系统的功率减小。在系统中加入串联补偿网络进行阻抗匹配,对系统进行校正,通过调节补偿系数来抵消了交叉耦合带来的影响,加入补偿网络后联列式(1)-(5).
式(14)给出了补偿元件的计算表达式,可以看出补偿元件为容性负载,根据谐振公式可算出对应的电容大小,表2给出了不同交叉耦合下的补偿元件值。
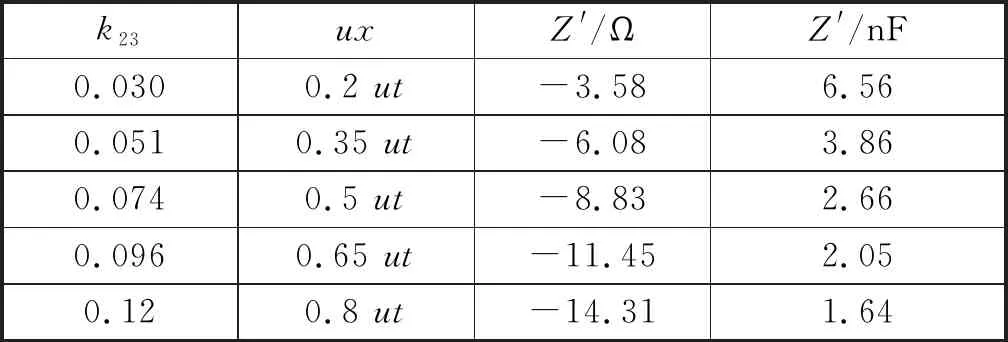
(14)
3 仿真实验及结果分析
分析表1中的数据可知,第一组与其他四组相比补偿电容相差很大,而第二与第三组数据比较,第四组与第五组比较,补偿电容相差不大,故选取第二组与第四组数据进行仿真分析,其余参数值取2.1节中的参数,取线径为1 mm的导线,缠绕成11 cm的线圈,缠绕圈数为3,根据电感计算公式可计算出电感L=2.8×10-6H,频率f=6.78 MHz.
根据图1(a)搭建仿真电路,仿真图形如图7所示。
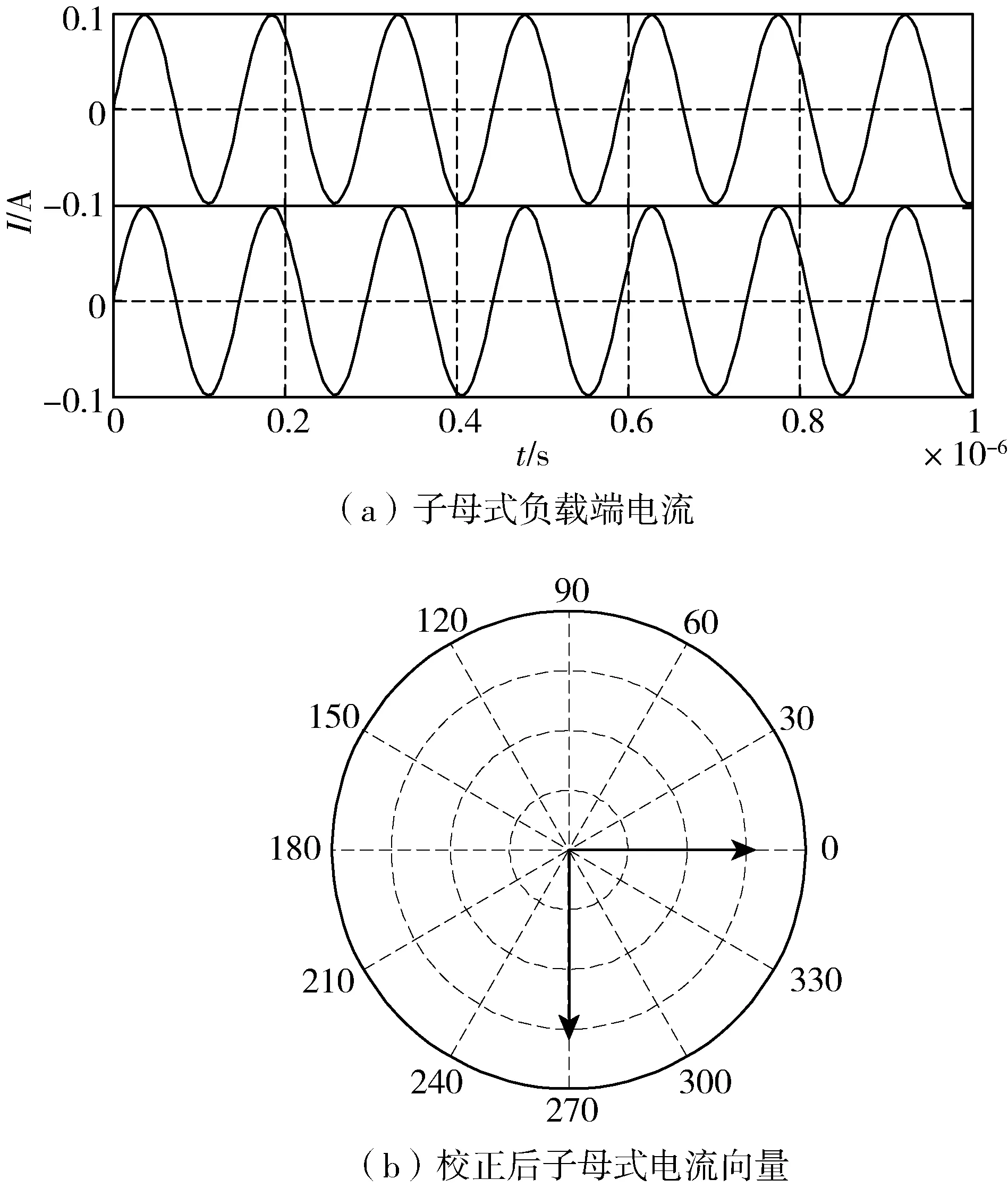
图6 校正后的电流仿真Fig.6 Calibrated current simulation
图6(a)为搭建仿真模型后得出的负载端电流仿真图,两个接收线圈的幅值大小和相位均相同,与图2的分析结果一致;图6(b)为加入补偿网络校正后的电流向量,实线为不考虑交叉耦合的理想电流向量,虚线为系统校正后的各线圈电流向量,与图2对比可知,系统加入了串串串(SSS)型补偿网络使电流向量的偏移情况得到了极大改善。
将补偿后的各参数带入式(7)、(8)中,得到的负载端电压和系统效率为图7所示。其中,图7(a)为负载端电压图,两条带有交叉耦合的负载端电压曲线与校正后的曲线比较发现,由于交叉耦合出现的谐振点偏移情况通过加入补偿元件得以校正,负载端电压有所提升;图7(b)为系统效率图,谐振点处的系统效率最大,两侧效率明显降低,系统谐振点校正后,系统效率较之前相比增大到65.36%,提高了系统能量传输能力,以上分析,证明所加入的补偿网络具有一定可行性。
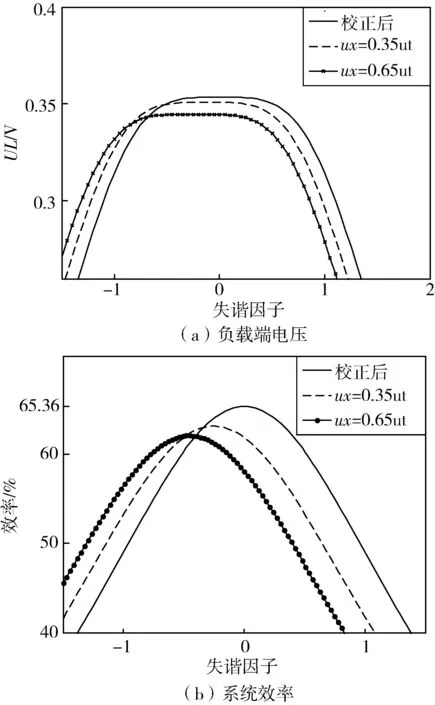
图7 校正前后负载端电压与系统效率Fig.7 Load terminal voltage and system efficiency before and after calibration
文献[14-16]指出,在各个参数都不改变的情况下,增加负载端个数可以提高系统的传输效率。针对子母式系统,在双负载的基础上增加接收系统组成多目标无线充电系统,去对应的n值,并利用式(8)求取系统效率,与双负载系统进行比较,发现效率与接收端个数成正比,图8为增加负载后的多目标系统效率对比图。
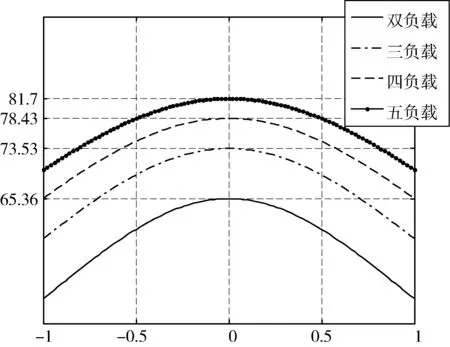
图8 不同负载个数系统效率Fig.8 System efficiency of different load systems
在图8中,三负载系统较双负载效率提升了8.17%,四负载系统较三负载系统增加4.9%,五负载系统增加3.27%,此时,多目标系统效率可达到81.7%,从四负载系统开始虽然每增加一个负载系统效率仍在增加,但增加幅度大幅减小,约为三负载系统增加率的一半,可见一个系统中的负载个数存在最优值,本文系统最佳负载个数为三个。
4 结论
对于多目标无线充电系统间存在的交叉耦合问题,根据对系统的数学模型的推导及一系列分析,可得到基本结论:
(1)交叉耦合使系统在谐振点的线圈电流、负载端电压幅值减小,相位发生偏移,也使得系统传输功率发生偏移,效率降低;
(2)在选取补偿网络解决交叉耦合问题时,采用寻找传输因式的最大值来确定补偿网络形式,仿真图形中传输因式的图形清晰简单,简化了推导过程中的数学计算;
(3)从校正后的电流向量、负载端电压和功率图形可以看出谐振点发生偏移的部分均得到校正,校正方法具有一定的可行性,且补偿推导基于基本的串并联补偿网络,计算简便有效又不失一般性,对多元补偿网络也具有借鉴意义;
(4)在解决交叉耦合问题的基础上,提出通过增加负载个数来提高系统效率的方法,针对本文的系统可知,负载最优个数为三个。

