求解大规模多目标问题的改进粒子群算法
兰丽尔,孙超利,何小娟,谭 瑛
(1.太原科技大学 应用科学学院,太原 030024;2.太原科技大学 计算机科学与技术学院,太原 030024 )
实际的工程应用领域[1]通常存在大量多目标优化问题,即优化问题需要同时考虑多个优化目标,而这些优化目标往往互相冲突。不失一般性,多目标优化问题的数学模型如下所示:
(1)
(2)
其中m表示优化目标个数,RD表示D维决策空间。通常,由于优化目标之间的冲突性,因此找不到一个最优解使得满足所有的目标函数达到最优,而找到的最优解通常不唯一且互相之间无优劣之分,故称为Pareto最优解集(Pareto-optimal set)或非支配解集(nondominated set)[2].
近年来,多目标进化优化算法,如多目标遗传算法[3]、多目标差分进化算法[4]以及多目标粒子群算法[5]等,由于能对整个搜索空间的大量可行解同时并行搜索,且对目标函数无连续可微要求等优点在求解多目标优化问题上获得了越来越多的应用。常见的多目标优化问题求解方法有基于支配关系的多目标优化方法、基于分解策略的多目标优化方法[6]以及基于指标的多目标优化方法[7]三大类。随着优化问题的复杂化,问题所需要优化的目标越来越多,计算也越耗时,因此近几年来,学者们专注于研究求解许多目标优化问题(Many Objective Problems,MaOP)的不同方法,如Wang等[8]提出了用于求解许多目标优化问题的偏好协同进化算法,Jain和 Deb[9]基于NSGA-II框架提出了NSGA-III算法,使用快速排序法进行分层并使用参考向量实现对下一代个体的选择,Li等[10]将支配和分解的方法结合,提出了一种基于分配和分解的多目标优化进化算法。Cheng等[11]提出了基于参考向量的进化算法,Zhang等[12]提出了基于拐点的进化算法,通过拐点增强多目标进化算法在求解许多目标优化问题的搜索性能。为了有效利用取样点的准确性用于计算IGD(Inverted Generational Distance)指标,Sun等[13]提出了一种有效的基于分解的最差点估计方法用于构建理想的Pareto前沿。
纵观现有的方法,大部分算法都是针对求解目标空间高维的问题而提出的。实际工程问题中,还存在决策空间高维的多目标优化问题。查阅以往文献,2017年由Zhang等[14]提出的基于决策变量聚类的进化算法用于求解大规模许多目标优化问题,2018年由Zille等人[15]提出的基于问题转化的大规模多目标优化。尽管这两种算法都取得了较好的优化效果,但是文献[14]中提出的方法运行时间较长,而文献[15]提出的方法中其分组机制以及转换函数会对结果产生影响。因此,急需新的求解大规模多目标优化问题的有效方法。
基于社会学习的粒子群优化算法是Cheng等[16]提出的用于求解大规模单目标优化问题的改进粒子群优化算法。在该方法中,每个粒子在每一维上向某一个比其好的个体的对应维以及种群的平均位置进行学习,在种群多样性和收敛性上取得平衡,从而获得大规模优化问题的最优解。2015年Cheng等[17]又提出了求解大规模单目标优化的粒子群算法,该算法采用一种竞争机制,在产生子代过程中失败者向成功者进行学习来更新粒子的位置和速度。之后2018年Zhang等[18]将该竞争机制引入大规模多目标优化问题中并取得了很好的成果。受此启发,本文基于分解策略的框架下将社会学习粒子群优化算法进行改进用于求解大规模多目标优化问题。在个体进化过程中,通过选择向沿当前权重向量更靠近参考点的个体学习,同时向更靠近权重向量的个体平均位置学习,以期能够为大规模多目标优化问题找到分布均匀的最优解集。
1 相关概念
1.1 基于社会学习的粒子群优化算法(SLPSO)
粒子群算法(PSO)[19]是Kenney和Eberhart为求解单目标优化问题而提出的,但是随着问题维度的提高,该算法在搜索过程中对于算法收敛性以及种群多样性很难平衡,而且在粒子搜索过程中容易早熟收敛,陷入局部最优。2015年,Cheng和Jin针对大规模优化问题提出了一种改进的粒子群算法,称为基于社会学习的粒子群优化算法(SLPSO)[16].在该算法中,对种群中的粒子根据适应值进行排序,除最优粒子之外,每个粒子的每一维向比其好的任一粒子以及种群的平均位置的相应维进行学习。图1给出了作为粒子i示范粒子的确定过程,N表示种群大小,式(3)和式(4)给出了粒子i在其j维上的更新公式。
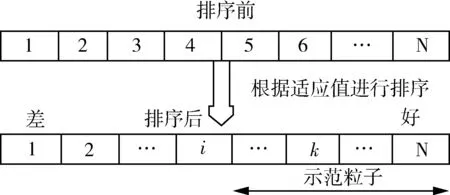
图1 示范粒子的确定Fig.1 Determination of demonstration particles
vi,j(t+1)=r1,j(t)*vi,j(t)+r2,j(t)*Ii,j(t)+r3,j(t)*ε*Ci,j(t)
(3)
xi,j(t+1)=xi,j(t)+vi,j(t+1)
(4)
其中
Ii,j(t)=xk,j-xi,j(t)
(5)
(6)

1.2 切比雪夫加权法(Tchebycheff Approach)

2 求解大规模的改进粒子群算法(MPSO)

(7)
(8)

图2 基于惩罚的边界交叉法示例Fig.2 Illustration of the penalty-based boundary intersection approach
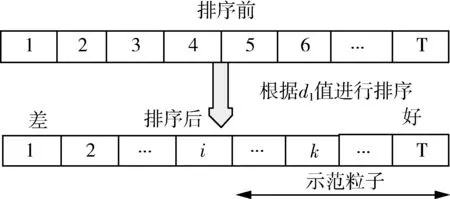
图3 个体沿权重向量方向与参考点的距离排序Fig.3 The distance between individuals along the weight vector direction and the reference point
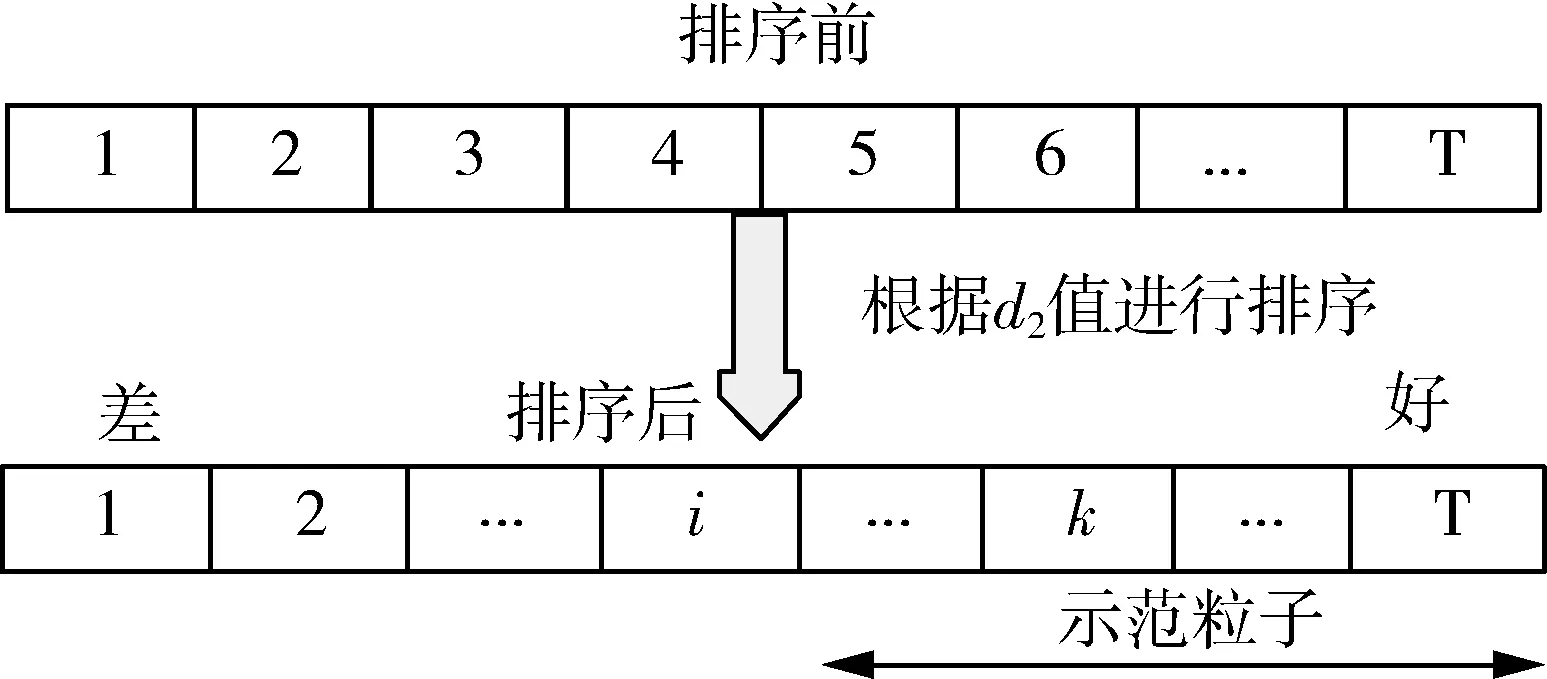
图4 个体与权重向量之间的距离排序Fig.4 Distance ranking between individuals and weight vectors
本文提出的算法具体步骤如下:
步骤1:
参数设定,包括种群大小,最大迭代次数,参考向量个数,邻域大小T;
步骤2:
初始化种群,包括初始化速度和位置;
步骤3:
步骤4:
产生权重向量,对每个权重向量分配种群个体;
步骤5:
确定每个个体i的邻域个体为B(i)={i1,…,iT};
步骤6:
对每个个体i,执行以下操作:
(1)对个体i及其邻域个体分别根据和d2进行排序,根据式(3)和式(4)对个体i使用本文所提方法进行速度和位置的更新;
(2)计算个体i的适应值和切比雪夫加权值,若比之前位置的切比雪夫加权值好,则保留现在的新位置,否则保留原有位置;
步骤7:
将当前种群个体和外部Archive中存储的非支配解集合并,重新更新Archive中的非支配解集;
步骤8:

步骤9:
是否满足终止条件,若满足,则输出;否则返回步骤5.
3 实验结果及分析
为了验证方法在大规模多目标优化问题上的有效性,我们选用5个ZDT测试函数,在低维和高维(500维和1000维)上进行了测试,并与传统的MOEA/D和NSGA-II进行了比较。MOEA/D和NSGA-II的测试结果在Tian等[21]提出的测试平台上运行得到。本文方法MPSO与这两种对比算法的种群大小均设置为100,MOEA/D与MPSO的邻域大小为20,而MOEA/D中模拟二进制交叉的分布指数和多项式变异都为20,交叉率为1,变异率为1/N.本文提出的MPSO算法中ε=β*g/MAXG,其中g表示当前代,MAXG表示最大迭代次数,在本文实验中,β=0.002,当维度低于100时,MAXG=250,维度大于100时,MAXG=500.β的取值由多次实验获得。每个算法在每个测试函数上独立运行20次。
为了对比不同算法的性能,在本文中采用IGD(Inverted Generational Distance)作为指标来评价不同算法的优化结果。假设P*是目标空间中最优 Pareto 面上均匀分布的点的集合,P是非支配解集,则IGD的定义为:
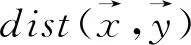
表1给出了本文算法以及MOEA/D和NSGA-II在低维上和高维(500维和1000维)上的统计结果,并给出了Wilcoxon秩和检验结果,“+”,“-”和“≈”分别表示MPSO算法的结果优于、差于和相似于对比算法得到的结果。从表1可以看到在低维多目标优化问题上,MPSO并不占优势,其获得的IGD结果均比不上MOEA/D和NSGA-II算法。而在500维和1000维上均获得了比其它两种方法更好的解,这说明本文算法在大规模优化问题上是有效的,这和文献中的结论也是相符的,也再一次验证了基于社会学习的粒子群优化算法在高维优化问题上的有效性。
表1 不同算法在不同维度测试函数上的统计结果
Tab.1 Statistical results of different algorithms on different dimension test functions

问题维度MOEA/DAvg.(Std.)NSGA-II Avg.(Std.)MPSOAvg.(Std.)ZDT13050010005.88E-03(2.47E-03)-5.55E+02(5.23E+01)+2.43E+03(9.98E+01)+4.77E-03(1.90E-04)-3.77E+02(4.12E+01)+1.70E+03(1.13E+02)+9.45E-02(1.06E-02)1.47E+01(3.81E+00)2.97E+02(1.43E+01)ZDT23050010001.41E-02(2.39E-02)-5.03E+02(4.84E+01)+2.38E+03(9.68E+01)+4.79E-03(2.01E-04)-3.84E+02(2.58E+01)+1.76E+03(1.12E+02)+1.03E-01(2.38E-02)2.37E+01(2.33E+00)1.95E+02(4.55E+01)ZDT33050010002.19E-02(1.31E-02)-5.75E+02(4.59E+01)+2.45E+03(8.40E+01)+4.85E-02(5.84E-02)-4.06E+02(3.72E+01)+1.71E+03(9.14E+01)+1.17E-01(4.83E-02)9.70E+00(7.88E-02)2.96E+02(2.95E+01)ZDT41050010008.51E-03(2.37E-03)-2.05E+03(8.96E+01)+6.49E+03(1.99E+02)+6.79E-03(2.02E-03)-1.72E+03(8.71E+01)+5.53E+03(1.95E+02)+9.57E-01(3.09E-01)1.68E+03(8.33E+01)4.91E+03(2.79E+02)ZDT61050010003.29E-03(8.22E-05)-2.51E+01(6.80E-01)+3.68E+01(6.10E-01)+3.85E-03(2.33E-04)-2.50E+01(5.35E-01)+3.49E+01(5.13E-01)+5.47E-02(1.15E-02)1.34E+01(1.92E-01)2.40E+01(1.09E+00) +/-/ 10/5/0 10/5/0
图5-9给出了不同算法在低维多目标优化问题上的IGD趋势图,从图中可以看出,在低维问题上,所提的MPSO算法在多样性和收敛性方面并不占特别的优势,但是在算法前期,除了ZDT4,本文所提出的MPSO算法相比于其它两种算法,具有较好的IGD值,说明通过本文方法在前期找到的最优解集具有较好的多样性和收敛性。
图10-14给出了不同算法在500维不同多目标优化问题上的IGD趋势图,从图中可以看出,本文所提的MPSO算法在相同评价次数下其IGD的值要远远好于其它两种算法。尽管在ZDT4上没有超过NSGA-II算法,但是相比于相应低维问题上的结果我们可以发现MPSO和NSGA-II之间的差距在逐步减少。
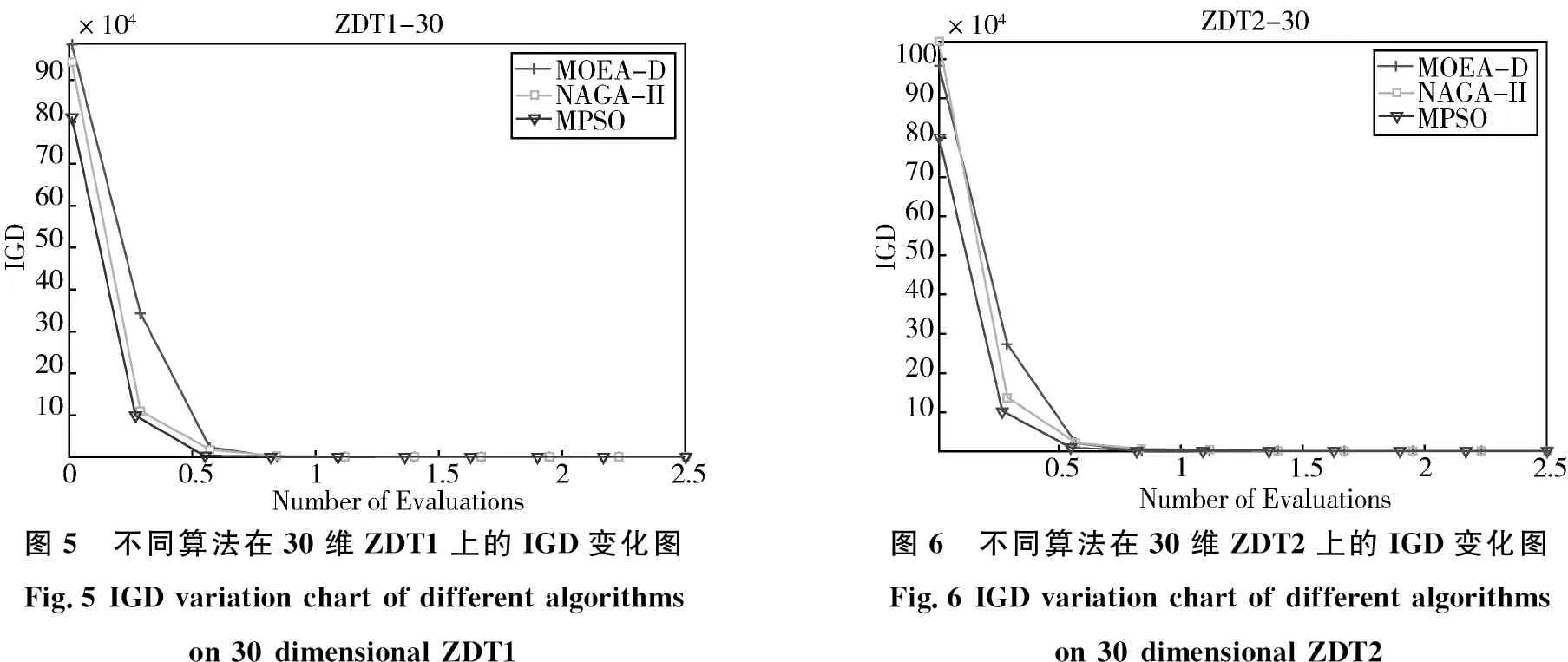
图5 不同算法在30维ZDT1上的IGD变化图Fig.5 IGD variation chart of different algorithms on 30 dimensional ZDT1图6 不同算法在30维ZDT2上的IGD变化图Fig.6 IGD variation chart of different algorithms on 30 dimensional ZDT2
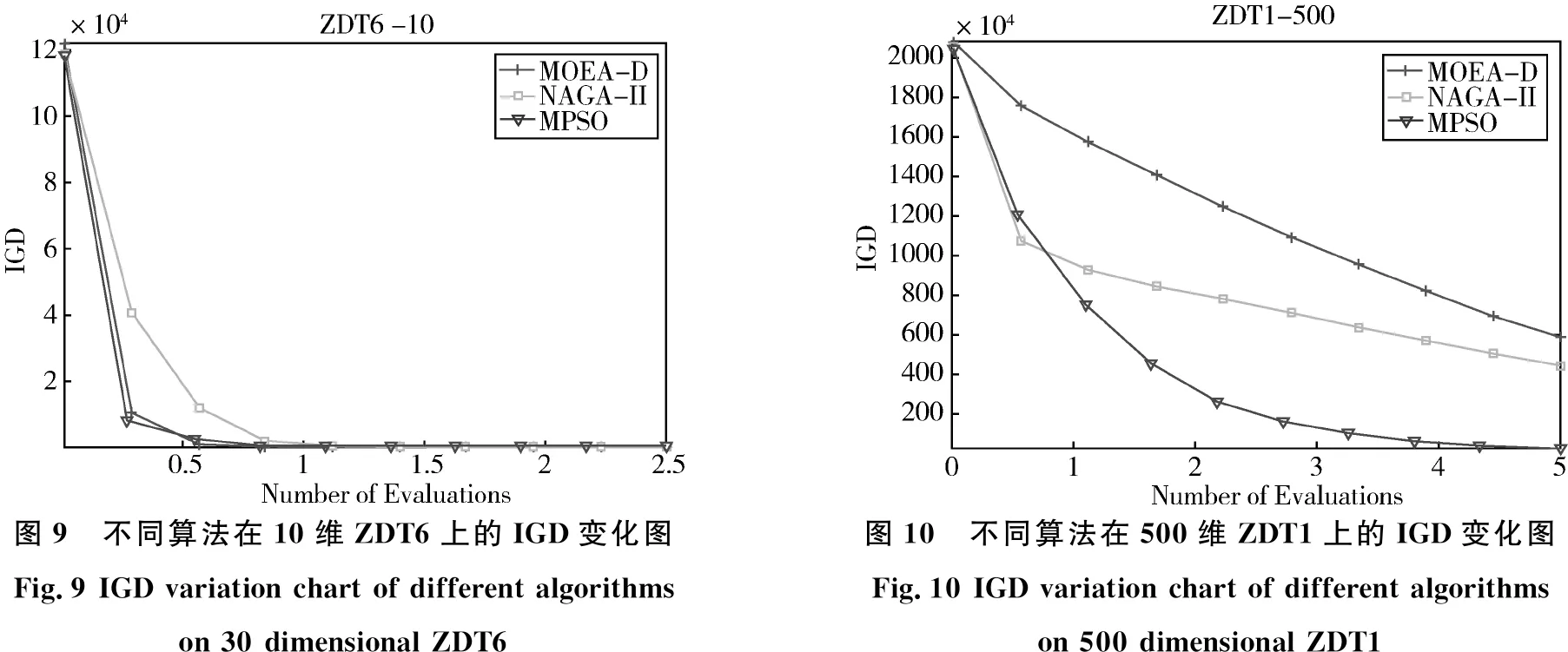
图9 不同算法在10维ZDT6上的IGD变化图Fig.9 IGD variation chart of different algorithms on 30 dimensional ZDT6图10 不同算法在500维ZDT1上的IGD变化图Fig.10 IGD variation chart of different algorithms on 500 dimensional ZDT1
图15-19给出了不同算法在1000维不同多目标优化问题上的IGD趋势图,从图中我们清晰地看到MPSO算法在每一次评价次数下其IGD的值均比其它算法好,特别是ZDT4上,我们很容易就发现本文所提出的MPSO在1000维ZDT4多目标优化问题上已获得了比其他算法更好的IGD值,再一次验证了本文算法在大规模多目标优化问题上的优势。
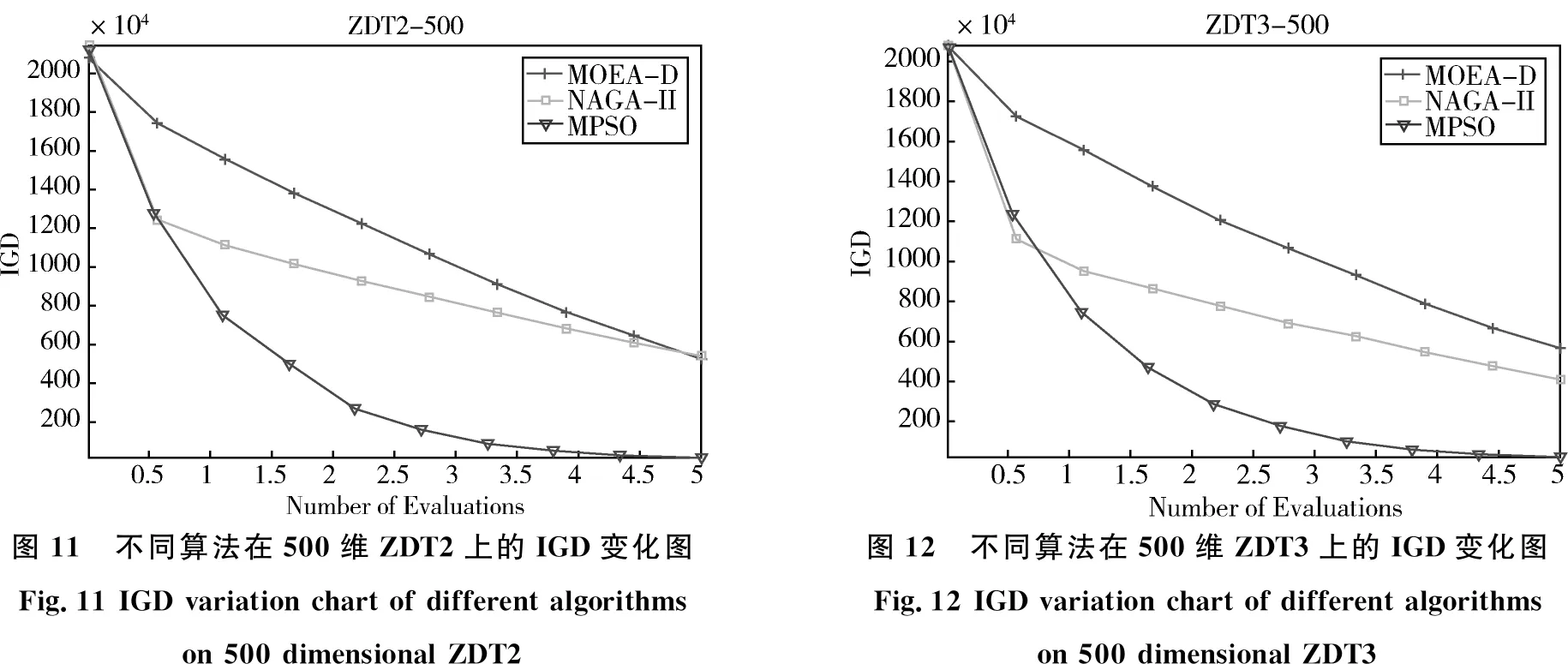
图11 不同算法在500维ZDT2上的IGD变化图Fig.11 IGD variation chart of different algorithms on 500 dimensional ZDT2图12 不同算法在500维ZDT3上的IGD变化图Fig.12 IGD variation chart of different algorithms on 500 dimensional ZDT3

图15 不同算法在1000维ZDT1上的IGD变化图Fig.15 IGD variation chart of different algorithms on 1000 dimensional ZDT1图16 不同算法在1000维ZDT2上的IGD变化图Fig.16 IGD variation chart of different algorithms on 1000 dimensional ZDT2
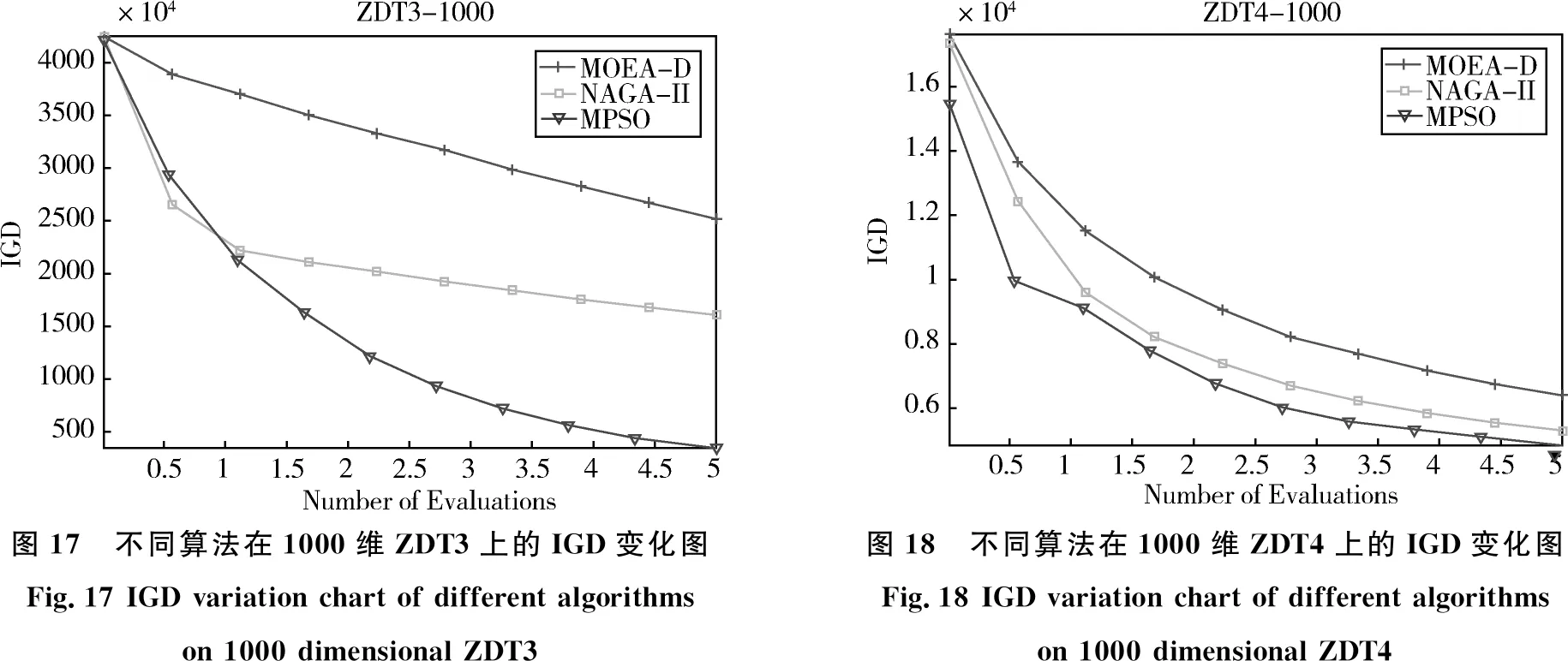
图17 不同算法在1000维ZDT3上的IGD变化图Fig.17 IGD variation chart of different algorithms on 1000 dimensional ZDT3图18 不同算法在1000维ZDT4上的IGD变化图Fig.18 IGD variation chart of different algorithms on 1000 dimensional ZDT4
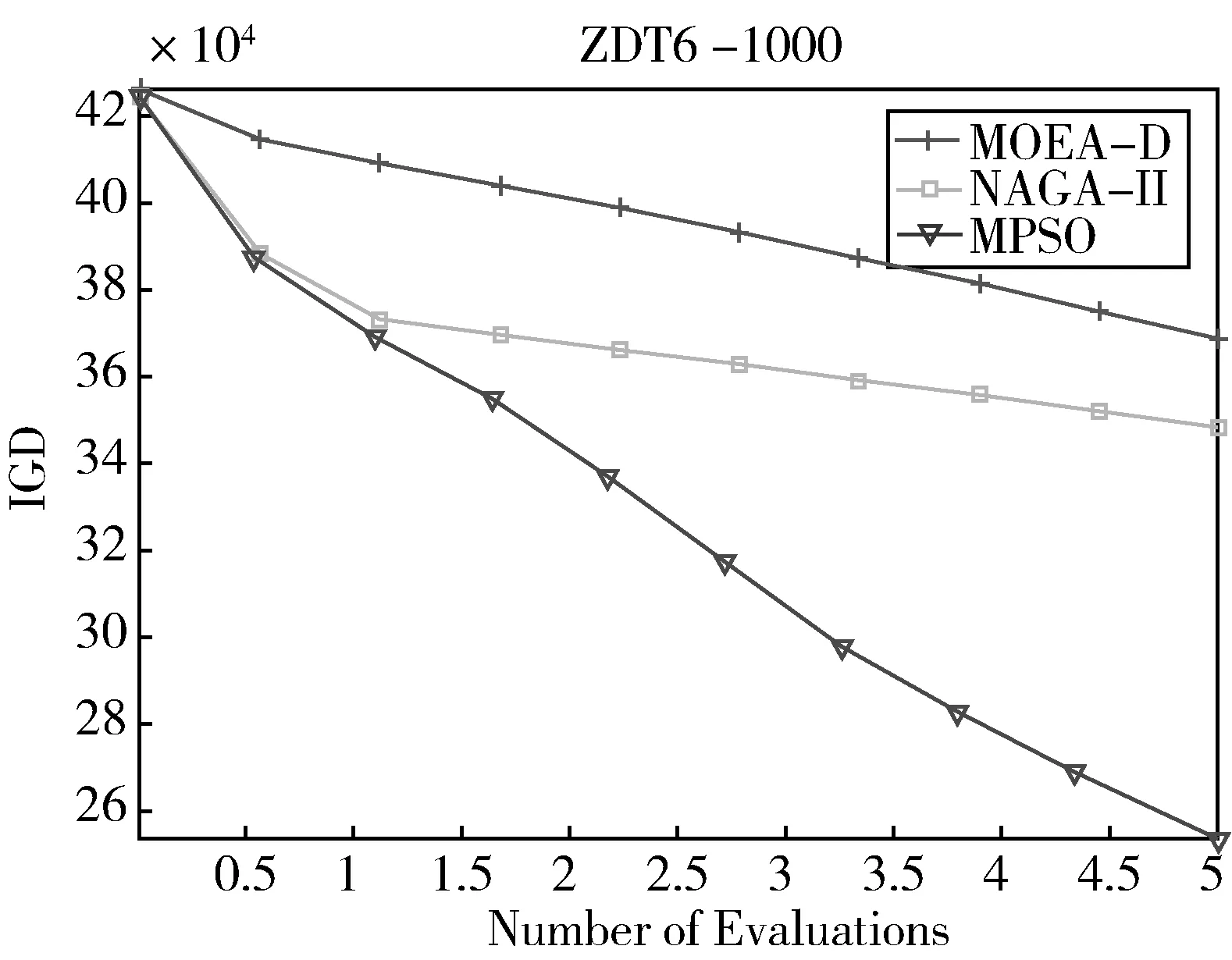
图19 不同算法在1000维ZDT6上的IGD变化图Fig.19 IGD variation chart of different algorithms on 1000 dimensional ZDT6
4 结论
针对大规模多目标优化问题,本文基于社会学习粒子群优化算法的思想,将多目标分解策略与之相结合提出了一种改进的粒子群算法(MPSO),并分别进行了低维和高维ZDT函数的测试,结果表明本文算法在求解大规模多目标优化问题上有明显的优势,但是在低维问题上并不理想。因此,今后将进一步改进算法,一方面保证在在低维问题上取得更好的结果,另一方面将其扩展到大规模许多目标问题中,以获得较好的最优效果。

