串级不稳定时滞过程的改进内模控制方法
王建鹏,张 森,刘 宁
(1.山西省自动化研究所,太原 030012;2.太原科技大学电子信息工程学院,太原 030024)
在工业过程中,有许多不稳定时滞被控过程,如工业反应器的温度控制和生化容器的液位调节,此类过程的输入和输出之间的平衡关系易受扰动影响[1],常规的控制方法难以取得满意的控制效果,为此出现了多种先进控制策略,如改进型PID控制[2-4]、优化控制[5-6]、二自由度控制[7-9]、串级控制[10-16]等,其中串级控制结构可以快速抑制混入中间级的干扰信号,近年来得到工业过程控制领域的关注并取得了一定的研究应用成果。文献[11]提出一种Smith结构,并对参数进行解析整定,但是控制结构比较复杂,且该控制结构只有一个自由度,无法兼顾动态特性以及干扰抑制特性。针对文献[11]的不足,文献[12]设计了一种二自由度的控制结构,并通过鲁棒性分析法对参数进行了整定,但计算比较复杂不利于工程应用。文献[13]设计了一种具有三个自由度的控制结构,系统的动态特性和干扰抑制特性获得很大改善,但系统结构复杂,设计难度大,不易实现。文献[14]提出了改进的Smith结构,与文献[13]相比该方法减少了控制器的个数,同时改善系统的控制性能,不过此方法需要整定的参数较多。随着内模控制方法的优点被广泛认可,大量内模相关的控制方法被应用到稳定过程控制中。目前,许多学者已经把内模控制方法进行了更深入研究,将其应用到不稳定过程的控制中。文献[15]在内模控制原理的基础上设计内外环控制器并转换成工程上常用的PID结构,引入设定值滤波器来减小系统的超调,但该方法的干扰抑制能力稍差。针对文献[15]中的不足,文献[16]结合内模控制和H2最优控制来设计控制器,利用最大灵敏度来整定参数,系统响应速度得到提高,但是会产生超调和振荡。
为解决上述问题,本文以内模控制原理为基础,采用一种新的串级控制结构,并给出相关控制器的设计方法。其中副回路采用内模控制结构,可以抑制副回路中的干扰;主回路采用二自由度结构,避免了设定值跟随特性与干扰抑制特性的折中,使系统同时获得较快地响应速度、较强的抗干扰能力和较好的鲁棒性。由于引入内模控制方法,各控制器的设计非常方便。通过理论论证以及仿真实验,证明了本章方法的有效性和优越性。
1 串级不稳定时滞过程的内模控制结构
基于内模的串级不稳定时滞过程二自由度控制系统结构如图1所示,其中r1,y1和d1分别为主回路的输入,输出和干扰信号;r2,y2和d2分别为副回路的输入,输出和干扰信号,P2(s)为副回路被控过程,P2m(s)为副回路被控过程的模型,Q2(s)为副回路内模控制器,P1(s)为主回路被控过程,Pm(s)为总的被控对象模型,Q1(s)为主回路内模控制器,C1(s)为设定值滤波器。
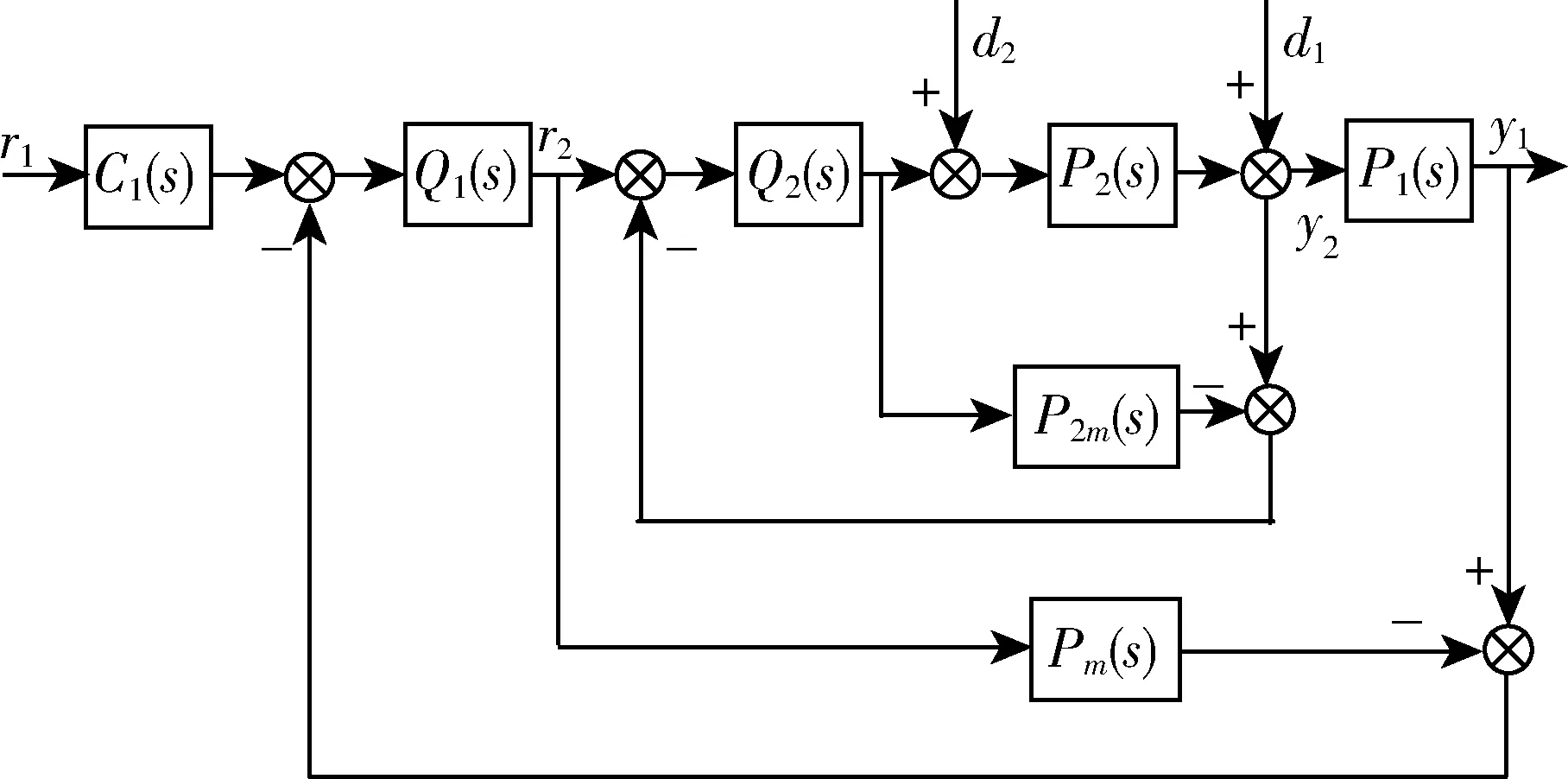
图1 串级不稳定时滞过程内模控制结构Fig.1 IMC structure of cascade unstable process with time delay
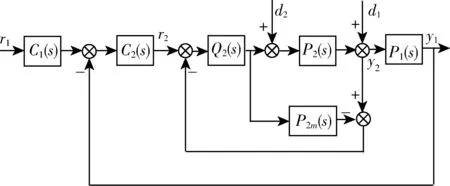
图2 等效控制结构Fig.2 Equivalent control structure
图1可等效变换为图2所示结构,其中C2(s)为主回路等效控制器,该控制器与内模控制器Q1(s)关系为:
(1)
副回路的设定值跟随特性和干扰抑制特性分别为:
(2)
(3)
当副回路被控过程模型精确时,即P2(s)=P2m(s),式(2)和(3)可化简为:
(4)
(5)
假设副回路无任何干扰,则主回路总的被控过程为:
P(s)=Q2(s)P2(s)P1(s)
(6)
由图2可得系统的输出为:
(7)
由式(7)可知,C2(s)单独控制着主回路的干扰抑制特性,C1(s)和C2(s)共同控制着主回路的设定值跟随特性。因此,在设计主回路控制器时应该先考虑C2(s),再设计设定值滤波器C1(s).
2 控制器设计
针对工业中较常见的一种串级不稳定时滞过程进行研究,其主副回路的过程分别为:
(8)
(9)
式(8)和(9)分别为一阶不稳定时滞过程和一阶惯性时滞过程,其中K1,K2,τ1,τ2,θ1,θ2分别是主副回路的比例增益、时间常数和时滞时间。
2.1 副回路控制器设计
依据内模控制原理设计副回路控制器:
(10)
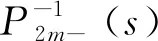
(11)
式中,λ2是滤波器时间常数。
将式(11)带入式(10)得控制器Q2(s)的表达式为:
(12)
式中,除λ2外均是已知参数,λ2的选取会影响系统的动态特性和鲁棒性。根据文献[14],λ2的取值范围一般为0.5θ2~θ2.
2.2 主回路反馈控制器设计
将式(8)、(9)和(12)带入式(6),得到系统主回路总的被控过程P(s)为:
(13)
式中:θ=θ1+θ2为系统总的时滞时间。
为了方便计算将上式改写为:
(14)
式中:K= -K1,τ= -τ1.
依据内模控制原理得Q1(s)为:
(15)
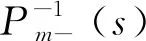
因为总过程P(s)中含有不稳定极点,考虑内模控制的稳定性要求,设计Q1(s)时应满足下列条件:
1)Q1(s)中没有不稳定极点;
2)Q1(s)GP(s)稳定;
3) [1-Q1(s)GP(s)]GP(s)稳定;
因为Q1(s)由式(15)计算得出,所以只要滤波器中没有不稳定极点就可保证前2个条件满足,为了满足第3个条件,低通滤波器f1(s)可选为:
(16)
式中:λ1为滤波器时间常数,通过调节λ1,可以改变系统的动态特性和鲁棒性,r一般取足够大以保证内模控制器Q1(s)的可实现性,m为P(s)中极点的个数,αi可由式(17)计算得出:
(17)
考虑到总过程模型为式(14)的形式,滤波器f1(s)选为:
(18)
则内模控制器Q1(s)为:
(19)
进一步可得C2(s)为:
(20)
考虑到上式不是经典PID控制器形式,不方便工程应用,本文采用1/1Pade近似逼近控制器中的时滞项,即e-θs=(1-0.5θs)/(1+0.5θs),得C2(s)为:
C2(s)=
(21)
从式(21)可以看出C2(s)为PID控制器串联高阶滤波器的形式,其中PID控制器的各个参数为:
(22)
串联滤波器的分子项和分母项分别为:
1+as=1+0.5θs
(23)
(24)
因为分母中的高阶部分对系统性能影响很小,可以将其忽略,因此只需计算出参数b即可,对式(24)两边求一阶导并令s=0可得:
(25)
式中:α1和α2可以通过式(17)计算得出,其中z1,z2分别为-1/τ,-1/λ2,则得:
α1=
(26)
(27)
另外,为了进一步改善系统的设定值跟随特性,减小超调,设计设定值滤波器
(28)
式中:0≤γ≤1,可以通过在线调整该参数的值来得到期望的设定值响应速度。
3 鲁棒性分析
实际工业控制中经常会出现模型参数摄动的情况,这时就要求系统应具有一定的鲁棒性。对主回路进行鲁棒性分析,考虑参数不确定的等效主回路过程P(s)包含于集合Π,即:
(29)
式中:u(s)为模型不确定性上界。令:
(30)
式中:Δm(s)表示被控过程与其模型的失配程度,由式(29)得系统鲁棒稳定的条件为:
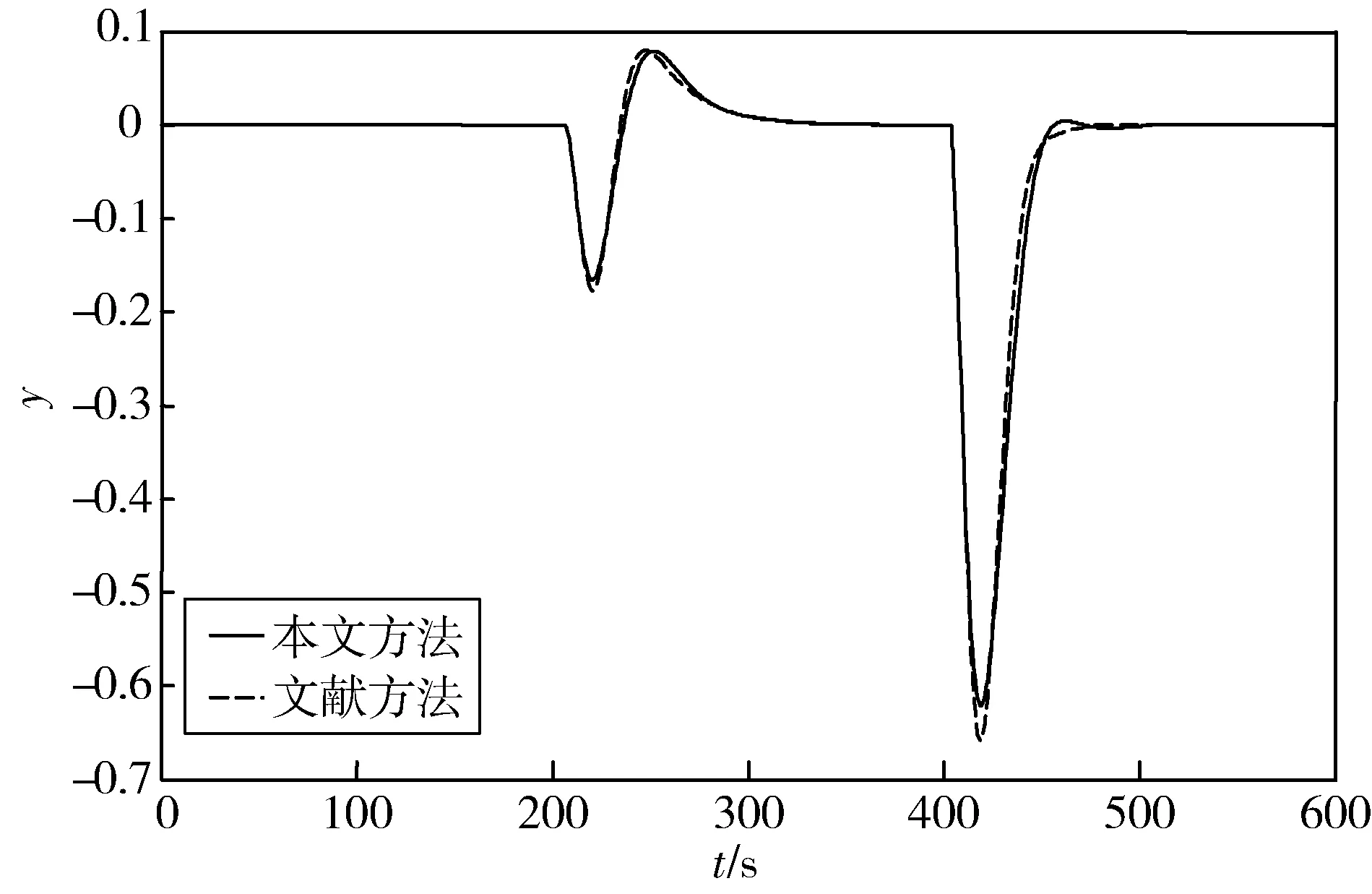
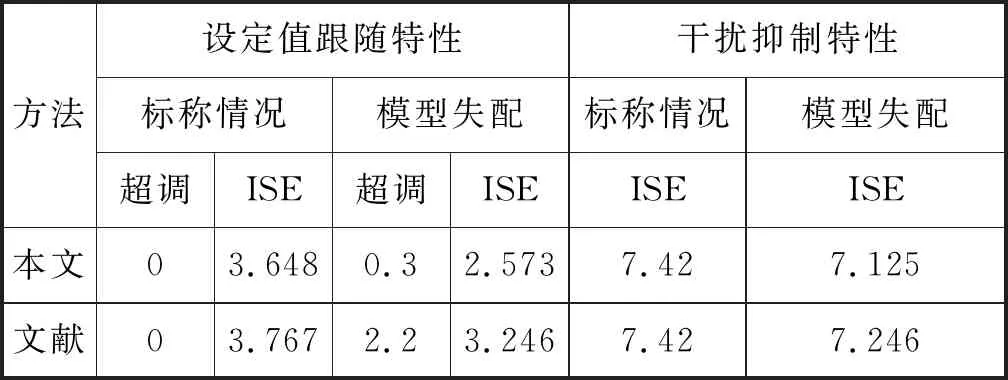
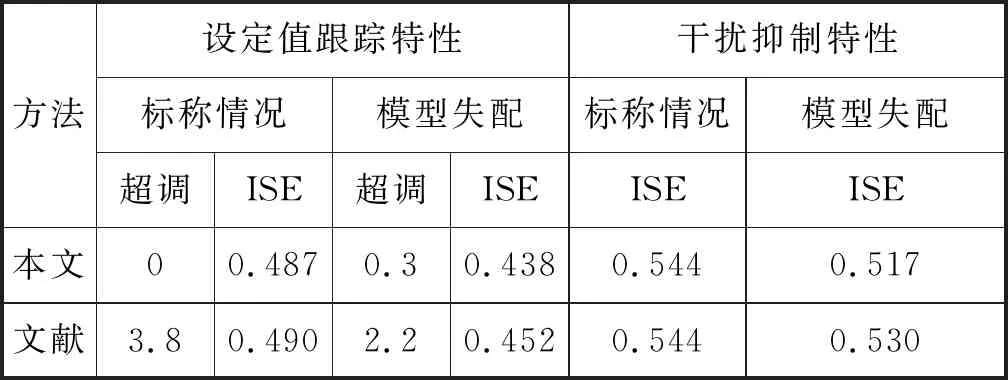
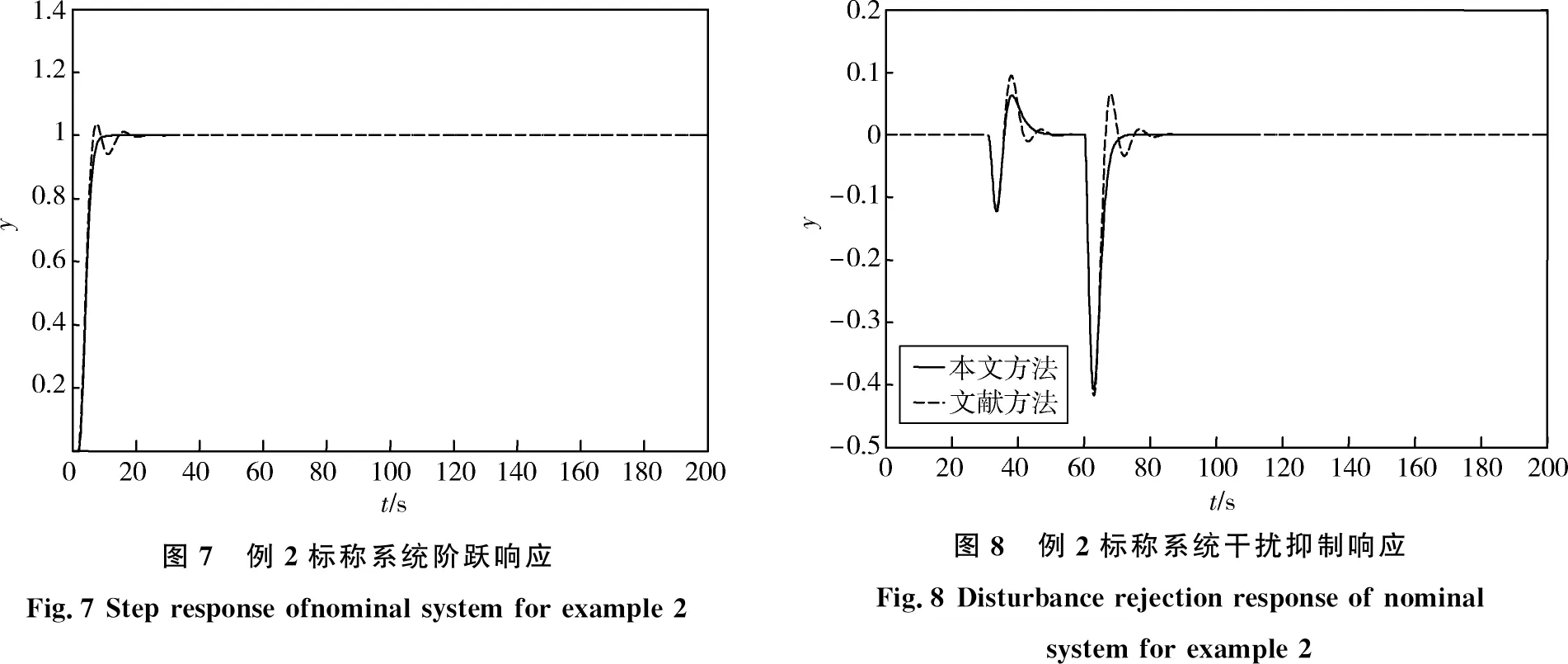
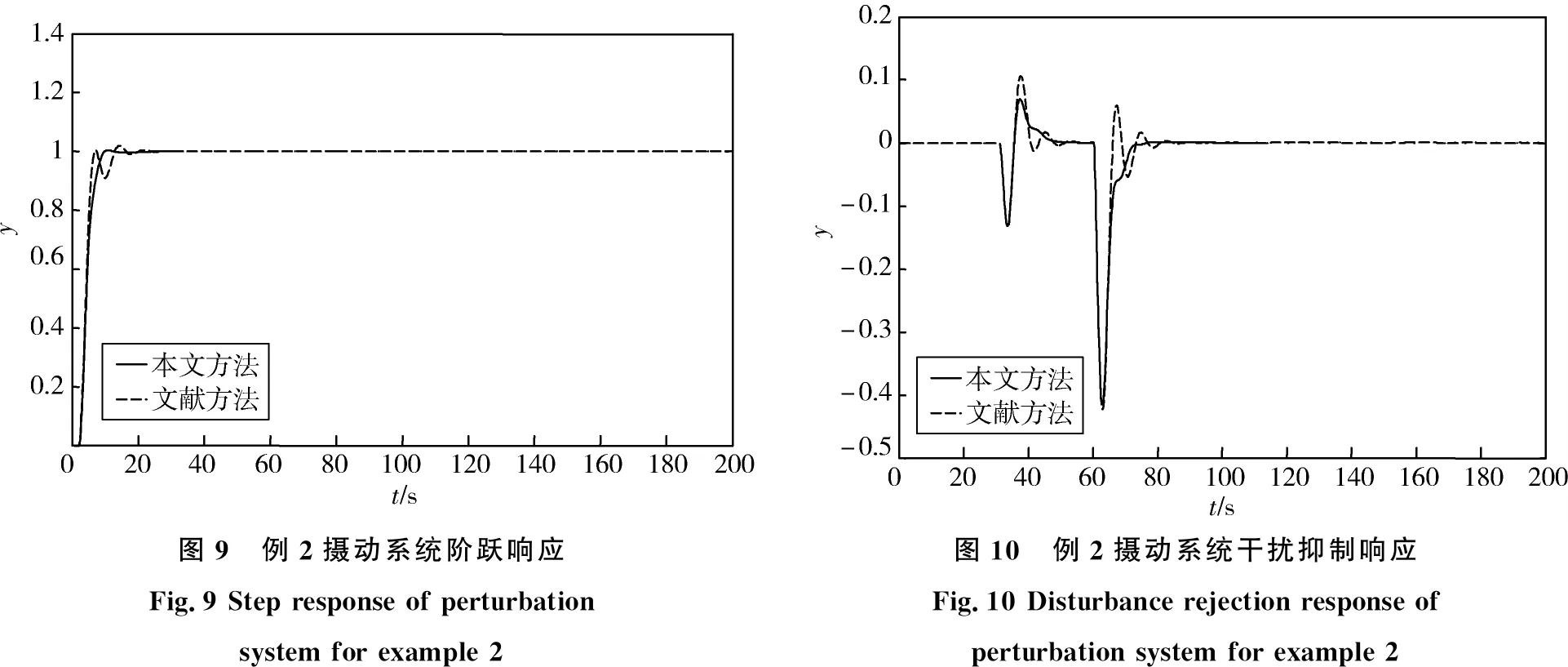
|Δm(s)| (31) 系统鲁棒稳定,则主回路过程的补灵敏度函数T(s)和模型不确定性上界必须满足: ‖T(s)u(s)‖<1 (32) 由式(31)和(32)得: ‖T(s)‖ (33) 由图2得系统的补灵敏度函数为: T(s)=Q1(s)Pm(s) (34) 将式(14),(16)和(34)代入式(33)得: (35) 假设主副回路存在不确定性ΔK1、ΔK2、Δτ1、Δτ2、Δθ1、Δθ2,则: (36) 将式(36)带入式(35),并令s=jω,这样就得到控制系统的鲁棒稳定性约束条件为: (37) 其中:∀ω>0. 结合式(26)、(27)、(37)可以看出,在λ2已经确定的前提下,针对过程中参数摄动情况,可以调节λ1来改变系统的鲁棒稳定性。考虑到补灵敏度函数越小系统的鲁棒性越好,即λ1较大系统的鲁棒性较好,反之λ1越小系统的鲁棒性越差。因此,在选择λ1时,需要同时考虑系统的鲁棒性和响应速度。 采用Matlab进行仿真研究来验证本文方法的有效性。考虑文献[16]的仿真实例并与其方法进行比较,选择系统的超调量δ%和ISE值作为控制性能指标,其值越小说明性能越优越。为了保证比较的公平性,先适当调整控制器参数使两种方法在标称情况下具有相同的ISE值,即两种方法具有相同的干扰抑制特性,然后分别比较系统的设定值跟随特性和参数摄动下系统的动态特性。 例1针对文献[16]中的串级不稳定时滞过程: 为了比较的公平性,文献[16]方法取其设计的参数,本文方法的控制器参数分别取为:λ1=4.786,λ2=2,γ=0.09,保证与文献[16]方法具有相同的干扰抑制特性,然后计算可得主副回路控制器、设定值滤波器的参数。控制系统的设定值输入信号为r(t)=1(t);干扰输入信号为d1(t)=-1(t-400),d2(t)=-1(t-200),即在时间t=200 s和400 s时,分别加入幅值为-1的阶跃干扰信号。系统的设定值跟随响应和干扰抑制响应分别如图3和4所示,控制性能指标如表1所示。由图3、图4和表1可知,标称情况下本文方法与文献[16]方法近乎相同,但性能指标仍略优于文献方法。 图3 例1标称系统阶跃响应Fig.3 Step response of nominal system for example1 图4 例1标称系统干扰抑制响应Fig.4 Disturbance rejection response of nominal system for example1 为了进一步验证系统的鲁棒性,假设被控过程参数产生摄动,K1、K2、τ1、τ2、θ1、θ2分别增大10%,设定值输入信号为r(t)=1(t);干扰输入信号为d1(t)=-1(t-400),d2(t)= -1(t-200).图5和6为参数摄动后两种方法的设定值跟随响应和干扰抑制响应,性能指标见表1,仿真结果表明本文方法具有更好的鲁棒性。 表1 例1控制系统性能指标 图5 例1摄动系统阶跃响应Fig.5 Step response of perturbation system for example1 图6 例1摄动系统干扰抑制响应Fig.6 Disturbance rejection response of perturbation system for example 1 例2针对文献[16]中的串级不稳定过程: 本文方法中的参数λ1=0.973,λ2=0.6,γ=0.2以保证标称情况下与文献[16]方法具有相同的干扰抑制特性。系统的设定值输入信号为r(t)=1(t),另外在时间t=30 s和60 s时,分别加入幅值为-1的阶跃干扰信号。图7和8分别为系统设定值跟随响应和干扰抑制响应,系统的性能指标如表2所示。 表2 例2控制系统性能指标 图7 例2标称系统阶跃响应Fig.7 Step response ofnominal system for example 2图8 例2标称系统干扰抑制响应Fig.8 Disturbance rejection response of nominal system for example 2 经过对比可以看出,本文方法可使系统更快达到设定值,且完全没有超调,在干扰输入作用下,本文方法能够更快地恢复稳定状态,表明本文方法具有较好的包含设定值跟随和干扰抑制的动态性能。为了对比鲁棒性,将系统参数K1、K2、τ1、τ2、θ1、θ2均增加10%,参数摄动后的设定值跟随响应和干扰抑制响应分别如图9和10所示,系统性能指标如表2所示。从仿真结果可以看出,当参数摄动时,本文方法可以更快达到设定值和抑制干扰,具有更好的鲁棒性。 图9 例2摄动系统阶跃响应Fig.9 Step response of perturbation system for example 2图10 例2摄动系统干扰抑制响应Fig.10 Disturbance rejection response of perturbation system for example 2 针对常见的一种串级不稳定时滞过程,设计了改进的内模控制方法,该方法内环采用内模控制结构,对副回路的干扰起到有效抑制的作用,外环在内模控制的基础上改进了滤波器的设计,使整个系统的干扰抑制特性得到增强,同时通过设定值滤波器进一步改善系统的设定值跟随特性。理论分析以及仿真结果表明,本文提出的控制系统结构简单,控制器参数整定方便,系统具备更好的动态特性和鲁棒性。4 仿真研究



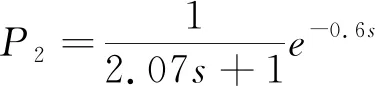
5 结论

