哥德尔不完全性定理的推广形式及其哲学影响

赵晓玉

1 引言

作为20 世纪逻辑学最为重要的成就之一，1930 年，哥德尔证明了关于递归可枚举理论的哥德尔不完全性定理1对几个说法略作说明：哥德尔第一不完全性定理指哥德尔证明的第一不完全性定理，哥德尔第二不完全性定理与此类似，哥德尔不完全性定理是哥德尔第一不完全性定理和哥德尔第二不完全性定理的概括；把哥德尔第一不完全性定理推广到非递归枚举理论上得到的定理称之为推广的哥德尔第一不完全性定理，推广的哥德尔第二不完全性定理与此类似，推广的哥德尔不完全性定理是推广的哥德尔第一不完全性定理和推广的哥德尔第二不完全性定理的概括；第一不完全性定理是哥德尔第一不完全性定理和推广的哥德尔第一不完全性定理的概括，第二不完全性定理与此类似，不完全性定理是哥德尔不完全性定理和推广的哥德尔不完全性定理的概括。。

定理1(哥德尔第一不完全性，1930).设T是包含罗宾森算术（Q）的、递归可枚举的理论。如果T是ω-一致的，那么存在一个Π1的语句ρ使得且。

定理2(哥德尔–罗瑟第一不完全性，1936).设T是包含Q 的、递归可枚举的理论。如果T是一致的，那么存在一个Π1的语句ρ使得且。

定理3(哥德尔第二不完全性，1930).设T是包含皮亚诺算术（PA）的、递归可枚举的理论。如果T是一致的，那么T不能证明自身一致性。

一个十分自然的问题便由是而生：哥德尔不完全性定理能否推广到非递归可枚举理论上？对此，已有一些研究成果。关于推广的哥德尔第一不完全性定理，

(1) 1975 年，R.G.Jeroslow 在[12，定理2]中证明了：如果T是包含PA 的、∆2-可定义的、一致的理论，那么T不是Π1-完全的。

(2) 1977 年，P.Hájek 在[8]中首先推广了Jeroslow 的结果：如果T是包含PA的、∆n-可定义的、一致的理论，那么T不是Πn−1-完全的。并同时证明了另外两个结果：如果T是包含PA 的、Πn-可定义的、n-一致的理论，那么T不是Πn−1-完全的；如果T是包含PA 的、Πn-可定义的、n-一致的理论，那么T不是Πn-决定的。

(3) 2016 年，S.Salehi 和P.Seraji 在[20]中进一步推广了Jeroslow 和Hájek 的工作，从而把哥德尔第一不完全性定理推广到了更一般的非递归可枚举理论上，但其推广工作并不十分充分。下文第3 节会对此进行清晰回顾，并就其关键定理给出更简洁易读的新证明，同时额外证明2 组结果。

关于推广的哥德尔第二不完全性定理，2018 年，我和Seraji 在[3]中进行了更一般的推广，但这部分工作也不充分。下文第4 节会对此进行简单回顾，并就其关键定理给出可读性更强的新证明，同时额外证明2 组结果。为了对哥德尔不完全性定理进行更充分的推广，下文第2 节会将哥德尔不完全性定理涉及的一致性、语法完全性、ω-一致性、相对于N的可靠性、相对于N的完全性、可定义性等元理论性质推广成更一般的形式，并对其性质进行深入研究。

第4 节所证推广的哥德尔第二不完全性定理都是有关Γ-可靠性的，而哥德尔第二不完全性定理却是涉及一致性的，那么是否存在涉及一致性的推广的哥德尔第二不完全性定理？下文第5 节将着重研究这个问题，并给出2 组可证自身一致性的理论。

哥德尔不完全性定理自被证明以来，在数学、哲学、计算机科学、物理学乃至宗教信仰等相关哲学问题上都产生了不同程度的影响。那么推广的哥德尔第二不完全性定理被证明以后，会对这些哲学影响造成什么样的改变？下文第6 节会基于推广的哥德尔不完全性定理，从对形式化方法局限的反驳、对反机械主义的支持、对数学家地位的辩护等三个方面重新审视这些哲学影响。

现在给出一些基本的记号、概念和命题，详见[9，19，23]。

记号1(算术语言、算术模型和算术片段).算术语言的非逻辑符号为S，+，×，0，其等词符号为；无歧义的情况下，既用n表示闭项Sn0，也用n表示某个自然数；x≤y被定义为∃z(z+x≃y)；关于皮亚诺算术PA 和罗宾森算术Q的公理，详见[19，第106 和234 页]；N=(N，S，+，×，≤，0)是标准算术模型；

引理1.设m，n ∈N。

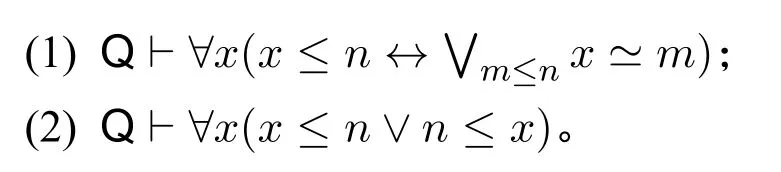
定理4(Σ1-完全性).设T是包含Q 的理论。任给Σ1语句ϕ，如果N⊨ϕ，那么T ⊢ϕ。

记号2(语法的算术化).是ϕ的哥德尔编码；公式caxmT(x)意为“x是有穷个T公理的合取”，而且caxmT(x)∈Σn当且仅当axmT(x)∈Σn；pf(y，x)是意为“在只有逻辑有效式作为公理的公理系统中y是x的证明”的∆0公式；pbT意为“x在T中是可证的”；¬(x)是由x解码后前缀¬得到的公式；Σn公式Σn-true(x)和Πn公式Πn-true(x)在N中分别定义{是Σn语句 且}和{是Πn语句 且}（详见[9，Corollary 1.76]）。

引理2(不动点).设T是包含Q 的理论，ϕ(x)是只含有自由变元x的公式。则存在某个语句ρ使得。其中ρ称为ϕ(x)的不动点。

定义3.设T是理论，Γ 是公式集。称Γ 是递归的，如果是递归的；称Γ 是递归可枚举的，如果是递归可枚举的，否则称Γ 是非递归可枚举的；称T是可公理化的，如果存在某个语句集Γ 使得T={ϕ | ϕ是语句且Γ⊢ϕ}；称T是递归可公理化的，如果存在某个递归的语句集Γ 使得T={ϕ|ϕ是语句 且Γ⊢ϕ}。

2 推广的元理论性质

在哥德尔–罗瑟第一不完全性定理2 和哥德尔第二不完全性定理3 中，都要求理论T是一致的，如下的Γ-一致性便是一致性的推广。

定义4(Γ-一致性).设T是理论，Γ 是一个语句集。称T是Γ-一致的，如果T+Γ 是一致的；否则，称T不是Γ-一致的。

哥德尔–罗瑟第一不完全性定理2 中的“不完全”是如下语法意义上的不完全。

定义5(完全性).设T是理论。称T是（语法）完全的，如果任给语句ϕ都有或或；否则，称T是（语法）不完全的。

如哥德尔–罗瑟第一不完全性定理2 所述，使得理论T不完全的语句是Π1的。为方便说明使得理论T不完全的语句的复杂度，定义如下概念。

定义6(Γ-决定性).设T是理论，Γ 是一个语句集。称T是Γ-决定的，如果任给语句ϕ ∈Γ 都有或或T ⊢¬ϕ；否则，称T不是Γ-决定的。

注1.哥德尔–罗瑟第一不完全性定理2 中的理论T不是Π1-决定的。

引理3.设T是理论。

(1) 如果T是Σn+1-决定的，那么T是Σn-决定的且Πn-决定的；

(2) 如果T是Πn+1-决定的，那么T是Σn-决定的且Πn-决定的；

(3)T是Σn-决定的当且仅当T是Πn-决定的；

(4) 如果T是完全的，那么T是Σn-决定的且Πn-决定的。

在哥德尔第一不完全性定理1 中，要求理论T是ω-一致的：称T是ω-一致的，如果不存在公式ϕ使得：(1)对某个ψ(x)有ϕ=∃xψ(x)，(2)T ⊢∃xψ(x)，(3) 任给m ∈N 都有T ⊢¬ψ(m)。实际上，由于使得理论T不完全的语句是Π1的，这个条件可以被弱化成：不存在ϕ ∈Σ1使得上述三个条件都成立。G.Kreisel 称这个条件为1-一致性（[13]），即如下n-一致性的特殊情形。

定义7(n-一致性).设T是理论，n ∈N。称T是n-一致的，如果不存在ϕ ∈Σn使得：(1)对某个ψ(x)有ϕ=∃xψ(x)，(2)T ⊢∃xψ(x)，(3)任给m ∈N 都有T ⊢¬ψ(m)；否则称T不是n-一致的。

引理4.设n>0 且T是理论。

(1) 如果T是n-一致的，那么T是一致的；

(2) 如果T是(n+1)-一致的，那么T是n-一致的；

(3) 如果T是ω-一致的，那么T是n-一致的且一致的。

注2.引理4 说明，ω-一致性是一致性的推广，而n-一致性是ω-一致性和一致性的推广。

任给ϕ，如果PA⊢ϕ都有N⊨ϕ。为方便表述类似于PA 的这种元理论性质，引入以下概念：

定义8(相对于N的可靠性).设T是理论。称T（相对于N）是可靠的，如果，任给语句ϕ如果T ⊢ϕ则N⊨ϕ；否则，称T（相对于N）是不可靠的。

类似地，相对于N的可靠性也可以进行推广。

定义9(相对于N的Γ-可靠性).设T是理论，Γ 是一个语句集。称T（相对于N）是Γ-可靠的，如果，任给语句ϕ ∈Γ 如果T ⊢ϕ则N⊨ϕ；否则，称T（相对于N）是Γ-不可靠的。

引理5.设T是理论。

(1) 如果T是Σn+1-可靠的，那么T是Σn-可靠的且Πn-可靠的；

(2) 如果T是Πn+1-可靠的，那么T是Σn-可靠的且Πn-可靠的；

(3) 如果T是Σn-可靠的，那么T是Πn+1-可靠的，从而也是Πn-可靠的。

(4) 如果T是可靠的，那么T是Σn-可靠的且Πn-可靠的。

证明.只证(3)。假设ϕ ∈Πn+1满足：对某个θ ∈Σn有ϕ=∀xθ(x) 并且T ⊢ϕ。则任给m ∈N 都有T ⊢θ(m)。再由Σn-可靠性可知，任给m ∈N 都有N⊨θ(m)。因此N⊨∀xθ(x)，即N⊨ϕ。

从哥德尔–罗瑟第一不完全性定理2 和哥德尔第二不完全性定理3 的表述上看，相对于N的Γ-可靠性看似是无关紧要的概念，实际上与Γ-一致性、n-一致性联系紧密。

引理6.设T是理论。

(1)T是可靠的当且仅当T是Th(N)-一致的当且仅当N⊨T；

(2)T是Σn-可靠的当且T是Πn(N)-一致的；

(3)T是Πn-可靠的当且仅当T是Σn(N)-一致的。

证明.只证(2)。(⇒)根据紧致性只需证：任给ϕ ∈Πn(N)，T+ϕ是可满足的。令ϕ ∈Πn(N)，则¬ϕ ∈Σn且。根据Σn-可靠性可知，因此T+ϕ是一致的，亦即可满足的。

(⇐)假定T不是Σn-可靠的，则存在某个ϕ ∈Σn使得T ⊢ϕ且。于是N⊨¬ϕ且¬ϕ ∈Πn，从而T+Πn(N)⊢¬ϕ。而由T ⊢ϕ可知T+Πn(N)⊢ϕ，这与T是Πn(N)-一致的矛盾。

引理7.设T是理论。

(1) 任给n ∈N，如果T是Σn-可靠的，那么T是n-一致的；

(2) 任给n ≥3，如果T是n-一致的，那么T不一定是Σn-可靠的；

(3) 任给n ∈N，如果T是n-一致的且Σn−1-完全的，那么T是Σn-可靠的。进一步令T包含Q，则

(4)T是Σ2-可靠的当且仅当T是2-一致的；

(5)T是Σ1-可靠的当且仅当T是1-一致的；

(6)T是Σ0-可靠的当且仅当T是一致的。

证明.(1)设对某个ψ ∈Πn−1有ϕ=∃xψ(x)∈Σn且T ⊢∃xψ。根据Σn-可靠性可知N⊨∃xψ(x)，从而对某个m ∈N 有N⊨ψ(m)，所以(m)。又由于¬ψ(m)∈Σn−1且T是Σn-可靠的，因此(m)。

(2)实际上，有更强的结论：ω-一致性推不出Σ3-可靠性（[11，Theorem 19]）。

(3)假设ϕ ∈Σn满足：对某个θ ∈Πn−1有ϕ=∃xθ(x)且(x)。根据n-一致性可知：对某个m ∈N 有(m)。又由于¬θ(m)∈Σn−1，因而根据Σn−1-完全性可得(m)，即N⊨θ(m)。因此N∃xθ(x)。

(4)–(6)由(1)可知只需证(⇐)，而这由(3)和T的Σ1-完全性易得。

注3.根据引理6 和7(6)可知，Γ-可靠性也是一致性的推广。

在哥德尔第二不完全性定理3 中，要求T是一致的，结论是T不能证明“T是一致的”，因而T是不完全的。又因为“T是一致的”可以转化为N中的真语句，所以这里“不完全”的含义实际上是如下意义的语义不完全。

定义10(相对于N的语义完全性).设T是理论。称T（相对于N）是语义完全的，如果，任给语句ϕ如果N⊨ϕ都有T ⊢ϕ；否则，称T（相对于N）是语义不完全的。

类似地，相对于N的完全性也可以进行推广。

定义11(相对于N的Γ-语义完全性).设T是理论，Γ 是一个语句集。称T（相对于N）是Γ-（语义）完全的，如果，任给语句ϕ ∈Γ 如果N⊨ϕ都有T ⊢ϕ；否则，称T（相对于N）是Γ-（语义）不完全的。

引理8.设T是理论。

(1) 如果T是Σn+1-完全的，那么T是Σn-完全的且Πn-完全的；

(2) 如果T是Πn+1-完全的，那么T是Πn-完全的且Σn-完全的；

(3) 如果T是Σn-完全的，那么T不一定是Πn-完全的；

(4) 如果T是Πn-完全的，那么T是Σn+1-完全的，因而也是Σn-完全的；

(5) 如果T是语义完全的，那么T是Σn-完全的且Πn-完全的。

证明.只证(3)和(4)。(3)Q 是Σ1-完全的但不是Π1-完全的（由哥德尔第一不完全性定理1 可知）。

(4)假设ϕ ∈Σn+1满足：对某个θ ∈Πn有ϕ=∃xθ(x)且N⊨ϕ。于是对某个m ∈N 有N⊨θ(m)，再由Πn-完全性有T ⊢θ(m)，因此T ⊢ϕ。

在哥德尔–罗瑟第一不完全性定理2 和哥德尔第二不完全性定理3 中，都要求理论T是递归可枚举的。仔细检查两个定理的证明过程不难发现，递归可枚举条件的主要作用是使得证明和可证性概念可以用算术语言表达。而把两个不完全性定理推广到非递归可枚举理论上，为保证证明和可证性概念可以用算术语言表达，就要求理论T必须是可定义的：

定义12(可定义性).设T是被语句集Ω 公理化的理论。称T是可定义的，如果存在某个公式axmT(x)使得Ω=且ϕ是语句}。

考虑到理论T公理集的复杂度，自然有如下推广的Γ-可定义性概念。

定义13(Γ-可定义性).设T是被语句集Ω 公理化的理论，Γ 是公式集。称T是Γ-可定义的，如果存在某个公式axmT(x)∈Γ 使得Ω={ϕ | N⊨axmT且ϕ是语句}。

引理9.设T是一个理论。

(1) 如果T是Σn-可定义的，那么T是Σn+1-可定义的且Πn+1-可定义的；

(2) 如果T是Πn-可定义的，那么T是Σn+1-可定义的且Πn+1-可定义的；

(3) 如果T是Σn+1-可定义的，那么T是Πn-可定义的；

(4)T是递归可枚举的当且仅当T是Σ0-可定义的当且仅当T是Σ1-可定义的。

证明.(1)和(2)显然成立；关于(3)，详见[20，Lemma 2.7]；关于(4)，由(3)可得“Σ1-可定义性⇒Σ0-可定义性”，“Σ0-可定义性⇒递归可枚举性”是平凡成立的。而由如下断言易得“递归可枚举性⇒Σ1-可定义性：如果T是递归可枚举的，那么T被某个递归集公理化（[4]）。

注4.引理9(4)说明，Γ-可定义性是递归可枚举性的推广。

为便于看出哥德尔不完全性定理是推广的哥德尔不完全性定理的特殊情形，本节用以上推广的元理论性质对哥德尔不完全性定理进行重述。根据引理9(4)和引理7(5)，哥德尔第一不完全性定理1 可以重述如下：

推论1.设T是包含Q 的理论。

(1) 如果T是Σ1-可定义的、1-一致的，那么T不是Π1-决定的。

(2) 如果T是Σ1-可定义的、Σ1-可靠的，那么T不是Π1-决定的。

由引理9(4)和引理7(6)，哥德尔–罗瑟第一不完全性定理2 可重述如下：

定理5.如果T是包含Q 的、Σ1-可定义的、Σ0-可靠的理论，那么T不是Π1-决定的。

由定理5，引理6 和引理7，哥德尔–罗瑟第一不完全性定理2 可重述如下：

推论2.设T是包含Q 的理论。

(1) 如果T是Σ1-可定义的、Π1-可靠的，那么T不是Π1-决定的。

(2) 如果T是Σ1-可定义的、可靠的，那么T不是Π1-决定的。

由引理9(4)和引理7(6)，哥德尔第二不完全性定理3 可重述如下。关于Σ0-Sound(T)和Π0-Sound(T)，参见下文。

推论3.设T是包含Q 的理论。

(1) 如果T是Σ1-可定义的、Σ0-可靠的，那么Σ0-Sound(T)。

(2) 如果T是Σ1-可定义的、Π0-可靠的，那么Π0-Sound(T)。

(3) 如果T是Π0-可定义的、Σ0-可靠的，那么Σ0-Sound(T)。

(4) 如果T是Π0-可定义的、Π0-可靠的，那么Π0-Sound(T)。

3 推广的哥德尔第一不完全性定理

Salehi 和Seraji 首先将推论2(2)推广到了非递归可枚举理论上。

定理6([20，Theorem 2.1]).如果T是包含Q 的、Σn-可定义的、可靠的理论，那么T不是Πn-决定的。

不难看出，定理6 对于Πn-可定义的理论也成立。

推论4.如果T是包含Q 的、Πn-可定义的、可靠的理论，那么T不是Πn+1-决定的。

Salehi 和Seraji 进一步把条件“可靠性”加强为Πn-可定义理论的Σn-可靠性或Σn-可定义理论的Σn−1-可靠性。这里给出新证明，与原证明相比，该证明更简洁易读，并且可额外证明N⊨ρ，而前者不能。

定理7([20，Theorem 2.4]).如果T是包含Q 的、Πn-可定义的、Σn-可靠的理论，那么T不是Πn+1-决定的。

证明.令

再令T∗=T+Πn(N)，则T∗是Πn-完全的、Σn+1-完全的，且根据Σn-可靠性是一致的。先证两个断言。

断言1.如果T ⊢δ，那么。

断言的证明.假定T ⊢δ。则对某个m ∈N 有。又由于且T∗是Πn-完全的，因而；根据T的一致性可知，因而任给k ∈N 都有。又由于Σn且T∗是Σn+1-完全的，因而任给k ∈N 都有；再根据引理1(1)可得。因此T∗⊢rpbT。

断言2.如果T ⊢¬δ，那么T∗⊢¬rpbT。

断言的证明.假定T ⊢¬δ。则对某个m ∈N 有。又由于∈Πn且T∗是Πn-完全的，因而。现在只需证

给定x。

现在回到定理的证明。令ρ为¬rpbT(y)的不动点，则

根据不动点引理中不动点的构造过程可知ρ ∈Πn+1。现在只需证ρ独立于T：如果T ⊢ρ，那么根据断言1 可得，但根据(2)却有T∗⊢，与T∗的一致性矛盾，因而；如果T ⊢¬ρ，那么根据断言2 可得，但根据(2)却有，也与T∗的一致性矛盾，因而。

可以进一步证明N⊨ρ。倘若，则N⊨¬ρ，又根据T∗的Σn+1-完全性和¬ρ ∈Σn+1可得T∗⊢¬ρ，矛盾。

推论5([20，Corollary 2.8 和2.9]).设n>1，T是包含Q 的理论。

(1) 如果T是Σn-可定义的、Σn−1-可靠的，那么T不是Πn-决定的；

(2) 如果T是Σn-可定义的、Σn-可靠的，那么T不是Πn-决定的。

条件“可靠性”也可以被加强为Πn-可定义理论的Πn+1-可靠性或Σn-可定义理论的Πn-可靠性。

定理8.如果T是包含Q 的、Πn-可定义的、Πn+1-可靠的理论，那么T不是Πn+1-决定的。

证明.根据引理5 可得。

推论6.如果T是包含Q 的、Σn-可定义的、Πn-可靠的理论，那么T不是Πn-决定的。

证明.根据引理9 和定理8 可得。

Salehi 和Seraji 进一步把条件Σn-可靠性加强为Πn-可定义理论的n-一致性或Σn-可定义理论的(n −1)-一致性。

定理9([20，Corollary 2.6]).如果T是包含Q 的、Πn-可定义的、n-一致的理论，那么T不是Πn+1-决定的。

推论7.设n>1，T是包含Q 的理论。

(1)（[20，Corollary 2.11]）如果T是Σn-可定义的、(n −1)-一致的，那么T不是Πn-决定的；

(2) 如果T是Σn-可定义的、n-一致的，那么T不是Πn-决定的；

(3) 如果T是Πn−1-可定义的、ω-一致的，那么T不是Πn-决定的；

(4) 如果T是Πn−1-可定义的、n-一致的，那么T不是Πn-决定的。

证明.(2)，(3)和(4)根据定理9 和引理4 可得。

Salehi 和Seraji 还证明n-一致性不能被加强为一致性。据此，还可以证明上述推广的哥德尔第一不完全性定理在推论8 的意义上是最优的。

定理10([20，Theorem 3.1]).如果T是包含Q 的、Σn+2-可定义的、一致的理论，那么T可能是完全的。

推论8([20，Corollary 3.4，无(2)和(5)]).设n>1，T是包含Q 的理论。

(1) 如果T是Σn-可定义的、Σn−2-可靠的，那么T可能是Πn-决定的；

(2) 如果T是Σn-可定义的、Πn−1-可靠的，那么T可能是Πn-决定的；

(3) 如果T是Σn-可定义的、(n −2)-一致的，那么T可能是Πn-决定的；

(4) 如果T是Πn−1-可定义的、Σn−2-可靠的，那么T可能是Πn-决定的；

(5) 如果T是Πn−1-可定义的、Πn−1-可靠的，那么T可能是Πn-决定的；

(6) 如果T是Πn−1-可定义的、(n −2)-一致的，那么T可能是Πn-决定的。

4 推广的哥德尔第二不完全性定理

定义14.设T是包含PA 的、可定义的理论。T的一致性可被形式化为：

由于Σn-可靠性等价于Πn(N)-一致性，所以Σn-可靠性可被形式化为：

其中，Πn-true(x)定义公式集Πn(N)。类似地，可将Πn-可靠性形式化。

注5.虽然Σn-可靠性与Πn(N)-一致性等价，但PA 不能证明Σn-可靠性与Πn(N)-一致性等价。

形式化完Γ-可靠性之后，我和Seraji 证明了推广的哥德尔第二不完全性定理11，该结果已发表（[3，Theorem 1]），但这里给出一种可读性更强的新证明。

引理10.设T是包含PA 的、可定义的理论。则任给公式ϕ都有

证明.在PA+Σn-Sound(T) 内推理：用反证法。不妨假设¬Σn-Sound(T+ϕ)且¬Σn-Sound(T+¬ϕ)，则存在s′，t′，u′，s′′，t′′，u′′使得

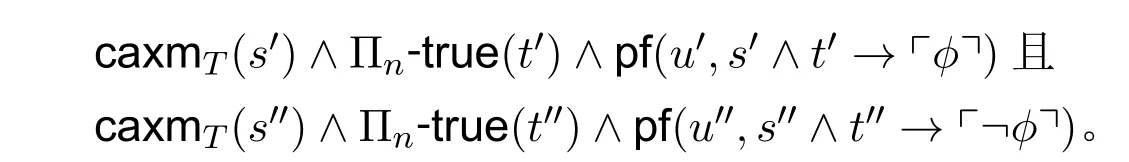
则对s=s′∧s′′，t=t′∧t′′和某个u有，即¬Σn-Sound(T)，矛盾！

引理11([1，Proposition 2.11]).设T是包含PA 的、可定义的理论。则任给公式ϕ ∈Σn+1，都有

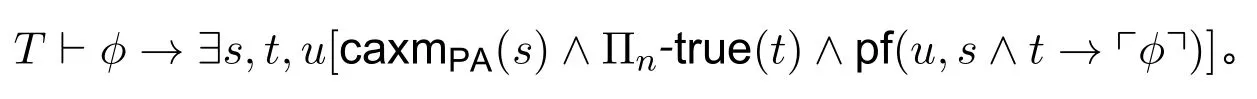
定理11.如果T是包含PA 的、Πn-可定义的、Σn-可靠的理论，那么Σn-Sound(T)。

证明.令T∗=T+Πn(N)，则根据T的Σn-可靠性可知：T∗是一致的且Σn+1-完全的（亦即Πn-完全的）。现在对如下定义的公式Σn-Sound(T+¬(x))运用不动点引理：

则存在一个不动点ρ ∈Πn+1使得

证明最终结论之前，先证三个断言。

断言3.T∗ρ。

断言的证明.假如T∗⊢ρ，则存在s，t，u ∈N 使得caxmT(s)∧Πn-true(t)∧是一个真的Σn+1语句。由于所有真的Σn+1-语句在Πn(N)⊆T∗中可证，所以T∗⊢¬Σn-Sound(T+¬ρ)，从而T∗⊢¬ρ，这与T∗的一致性矛盾！

断言4.T∗⊢Σn-Sound(T+ρ)→ρ。

断言的证明.根据引理11 可知，任给ϕ ∈Σn+1都有

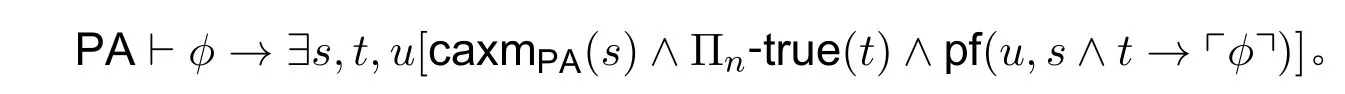
因而

又由于N⊨∀x(axmPA(x)→axmT(x))（T是PA 的扩张）和∀x(axmPA(x)→axmT(x))∈Πn，因而根据T∗的Πn-完全性可得

断言5.T∗+Σn-Sound(T)⊢ρ。

断言的证明.假如T∗+Σn-Sound(T)，则根据(3)可得

根据断言4 可得

根据引理10 可得

综合(6)、(7)和(8)可得T∗+Σn-Sound(T)⊢ρ，矛盾，所以原结论成立。

回到定理的证明。不妨假设T ⊢Σn-Sound(T)。则T∗⊢Σn-Sound(T)，因而根据断言5 可得T∗⊢ρ，与断言3 矛盾。因此Σn-Sound(T)。

推论9([3，Theorem 2]).如果T是包含PA 的、Σn+1-可定义的、Σn-可靠的理论，那么Σn-Sound(T)。

实际上，按照证明定理11 的证明方法也可以证明Πn-可靠性相关的情形。

定理12.如果T是包含PA 的、Πn-可定义的、Πn+1-可靠的理论，那么Πn+1-Sound(T)。

推论10.如果T是包含PA 的、Σn+1-可定义的、Πn+1-可靠的理论，那么Πn+1-Sound(T)。

证明.根据定理12 和如下事实：任给Σn+1-可定义的理论T，都有一个与之等价的理论T′使得PA⊢Πn+1-Sound(T)↔Πn+1-Sound(T′)。

上述推广的哥德尔第二不完全性定理在如下结果的意义上是最优的。定理13 的证明方法也适用于定理14。

定理13([3，Theorem 3]).任给n >0，都存在一个包含PA 的、∆n+1-可定义的、Σn−1-可靠的理论T 使得T⊢Σn−1-Sound(T)。

推论11.任给n >0，都存在一个包含PA 的、Πn-可定义的、Σn−1-可靠的理论T 使得T⊢Σn−1-Sound(T)。

定理14.任给n>0，都存在一个包含PA 的、∆n+1-可定义的、Πn-可靠的理论S 使得S⊢Πn-Sound(S)。

推论12.任给n>0，都存在一个包含PA 的、Πn-可定义的、Πn-可靠的理论S 使得T⊢Πn-Sound(S)。

5 非递归可枚举理论与形式化的一致性

上述推广的哥德尔第二不完全性定理都是有关Γ-可靠性的，那么涉及一致性的推广的哥德尔第二不完全性定理是否成立？不妨假设成立，比较自然的证明思路是仿照哥德尔第二不完全性定理的证明思路：先证明满足一定条件的理论T满足三个可证条性条件，再证明它不能证明自身一致性。

定义15 (可证性关系).设T是可定义的理论，ϕ是任意公式。令

定义16(可证性条件).设T是可定义的理论，ϕ，ψ是任意公式。三个可证性条件为：

现在考察非递归可枚举理论T需要满足的条件，除了Σn-可定义性之外，不妨假设其它条件与哥德尔第二不完全性定理相同，即T是包含PA 的、Σn-可定义的、一致的理论。研究发现，这样的理论并不一定满足所有的可证性条件：

引理12.设n>1。如果T是包含PA 的、Σn-可定义的、一致的理论，那么T不一定满足D1。

证明.构造反例：给定公式ϕ满足T ⊢ϕ，则对某个m ∈N 有，因而，即。注意，，因此只需要令。

因此需要强化非递归可枚举理论T需要满足的条件。鉴于引理12，要求T是Σn-完全的便是一个可行的选择。经过研究发现，此时的理论T满足所有的可证性条件。

引理13.如果T是包含PA 的、Σn-可定义的、一致的、Σn-完全的理论，那么T满足D1。

证明.仿照[23，引理10.1.2]的证明。

引理14.如果T是包含PA 的、Σn-可定义的、一致的理论，那么T满足D2。

证明.仿照[23，第10.2 节]中递归可枚举理论满足D2的证明。

引理15.如果T是包含PA 的、Σn-可定义的、一致的、Σn-完全的理论，那么T满足D3。

证明.仿照[23，第10.3 节]中递归可枚举理论满足D3的证明。

把引理13、14、15 中的“Σn-可定义的”改为“Πn−1-可定义的”，或把“Σn-完全的”改为“Πn−1-完全的”，类似地可以证明其余3 组结论。

因此对于满足一定条件的非递归可枚举理论来说，改编哥德尔第二不完全性定理的证明即可得知它也不能证明自身的一致性，这是一种证明方法。下面给出第二种证明方法，即，将这些结论作为第4 节所证推广的哥德尔第二不完全性定理的直接推论。

推论13.如果T是包含PA 的、Πn-可定义的、一致的、Πn-完全的理论，那么Con(T)。

证明.显然T=T+Πn(N)，因而T是Σn-可靠的。由于T是一致的，根据定理11 可得Σn-Sound(T)。又由于Σn-Sound(T)Con(T+Πn(N))=Con(T)，因此Con(T)。

推论14.如果T是包含PA 的、Σn+1-可定义的、一致的、Πn-完全的理论，那么Con(T)。

证明.将推论13 证明中的定理11 改为定理9 即可。

推论15.如果T是包含PA 的、Πn-可定义的、一致的、Σn+1-完全的理论，那么Con(T)。

证明.根据推论13 和引理8 可得。

推论16.如果T是包含PA 的、Σn+1-可定义的、一致的、Σn+1-完全的理论，那么Con(T)。

证明.根据推论14 和引理8 可得。

如下结果表明了上述涉及一致性的推广的哥德尔第二不完全性定理是最优的，同时给出了两组可证自身一致性的理论。

推论17.任给n>0，都存在一个包含PA 的、∆n+1-可定义的、Πn−1-完全的理论T 使得T⊢Con(T)。

证明.将所有公式枚举为χ0，χ1，χ2，...，其中χ0=Con(T0)。如下递归地构造T：T0=PA+Πn−1(N)；如果Ti+χi是一致的，令Ti+1=Ti+χi，否则令Ti+1=Ti+¬χi；T=∪i∈NTi。在[3，Theorem 3]中，证明了T 是∆n+1-可定义的、Σn−1-可靠的理论，同时T⊢Σn−1-Sound(T)。又因为Πn−1(N)⊆T，因此T 是Πn−1-完全的，而且由Σn−1-Sound(T) ≜Con(T+Πn−1(N))=Con(T)可得T⊢Con(T)。

推论18.任给n>0，都存在一个包含PA 的、∆n+1-可定义的、Σn-完全的理论S 使得S⊢Con(S)。

证明.将推论17 证明中的Πn−1(N)改为Σn(N)即可。

6 推广的哥德尔不完全性定理产生的哲学影响

6.1 对形式化方法局限的反驳

所谓形式化方法是现代一阶逻辑意义下的一种方法，其具体过程为：给定一个公理化的理论T（这里并不要求公理集是递归的），如皮亚诺算术；建立一个包括逻辑符号和非逻辑符号的一阶语言，非逻辑符号应当与理论T中的某些基本概念对应起来，如应备有符号以分别表示加法函数、减法函数、小于关系、0、1、2、……等等；建立语法，明确什么是项和公式；建立语义，准确定义什么是真；建立一阶逻辑公理系统，包括公理集和推理规则；在一阶逻辑公理系统中定义什么是证明；把T的公理加入一阶逻辑公理系统的公理集。

在哥德尔不完全性定理被证明后，不少学者将递归可枚举理论的不完全性现象归结为形式化方法的局限，比如J.W.Dawson、王浩（H.Wang）、H.-D.Ebbinghaus 等人。Dawson 在1999 年发表了一篇文章，除了讲述哥德尔的生平，还重点谈及哥德尔完全性定理和不完全性定理。他将这篇文章的标题拟为“Gödel and the limits of logic”（[5]），其中“the limits of logic”指的便是形式化方法的局限；王浩曾在其专著《逻辑之旅》中说（[24，第90 页]）：

这些结果包括(1)他对谓词逻辑完全性的证明（1929 年）；(2)对任何数学形式系统构造一个在该系统中不可判定的数论问题的方法（1930 年）；(3)任何古典数学形式系统的一致性在同一系统中不可证的证明（1930 年）……完全性定理(1)可被视为一个成功的结论，肯定了我们对哥德尔称之为“有穷心灵的逻辑”有了令人满意的精确描述。这一定理也对不完全性定理(2)和(3)作了补充，从而证明机械化和具体直觉有作用但也有局限性……

其中的(2)指的是哥德尔第一不完全性定理1，(3)指的是哥德尔第二不完全性定理3，而“机械化”则与“形式化”含义相同；Ebbinghaus 等人曾在其编著《数理逻辑》中说（[6，第186 页]）：

Intuitively this means that there is no decidable consistent system of axioms for mathematics which，for every mathematical statement，allows us to either prove or disprove it.In this fact an inherent limitation of the axiomatic method is manifested.

其中的“axiomatic method”即公理化方法，此处含义与形式化方法相同。不仅如此，其第10 章更直接以“Limitations of the Formal Method”为题（[6，第151页]）。显然，Ebbinghaus 等人认为不完全性现象是形式化方法本身固有的局限。

在本文作者看来，将不完全性现象归结为形式化方法的局限是不合适的。下面以第一不完全性定理为例对此进行论证，第二不完全性定理的情形与此类似。如定理5 所言，足够强的、一致的递归可枚举理论是不完全的。虽然如推论5(1)所言，足够强的、一致的非递归可枚举理论满足一定条件也是不完全的，但是改变这些条件，足够强的、一致的非递归可枚举理论却可以是完全的：无论是可定义的——如定理9 中的理论，还是不可定义的——如理论Th(N)。换言之，之所以出现不完全性现象，是对理论性质的要求使然，而非形式化方法的问题。因此，不完全性现象是偶然而非必然的，从而也就不能将其归结为形式化方法的局限。

6.2 对反机械主义的支持

作为机械主义（mechanism）的代表人物，T.Hobbes（见[10]）、J.O.de La Mettrie（见[14]）等人认为人的心灵（mind）用神经系统的物理操作足以解释，因而是一台机器。在某种程度上可以称为某种机械主义的计算主义（computabilism），在这方面更进一步，认为大脑（brain）和心灵基本像一台计算机一样工作（见[24，第231 页]）。而作为反机械主义（antimachanism）的代表人物，N.Malcolm（见[16]）、D.Chalmers（见[2]）等人则基于与心灵、意识和自由意志相关的常识提出了反驳：心灵哲学层面，他们认为非意识部分不足以解释意识现象；形而上学层面，他们认为机械主义会导致有关人类行动的决定论，而这与通常认为的“人是有自由意志的动物”相矛盾。

哥德尔不完全性定理在被证明以后成为了反驳机械主义尤其是计算主义的有力武器。利用哥德尔不完全性定理进行反驳的有哥德尔、J.R.Lucas、R.Penrose 等人2Lucas 的论证（[15]）与哥德尔的论证相似，这里只论述哥德尔的论证；而Penrose 的论证虽说也与哥德尔的论证有相似之处，但差别较大且与第6.3 节内容联系密切，故将其放在第6.3 节。。哥德尔认为大脑在某种程度上的确是一台机器（计算机）（[24，第231 页]），但却不认为心灵是一台机器，并认为心灵胜过所有的机器，他借助哥德尔第二不完全性定理和理性乐观主义对此进行了论证3详见[22，第324–326 页]或[24，第231–241 和416–419 页]，该论证过程始于1951 年的[7]，终于1972 年的[22，第324–326 页]。为使哥德尔的论述看上去是一个完整的论证，本文作者将其按如下方式排放，同时为增强可读性还添加了四处［］内的注释。：

心灵不能将它所有的数学直觉都形式化（或机械化）。这就是说，如果它成功地形式化了其中一些直觉，那么这件事实本身又生出了新的直觉性知识，比如这个形式化的一致性。［这里运用了与哥德尔第二不完全性定理3等价的论断：如果一台足够强的定理证明机器是一致的，那么它不能证明表达其自身一致性的语句］这可以称为数学的“不可完全性”。另一方面，基于迄今已证明的结果，有可能存在（甚至可以在经验中发现）一台定理证明机器，它事实上等价于数学直觉，但不能被证明如此，甚至不能证明对有穷数论它只产生正确的定理。

［鉴于上述考察，我们可以知道］或者心灵胜过所有的机器（说得确切一些，它比任何机器都能判定更多的数论问题），或者存在一些心灵不能判定的数论问题。（不排除二者都真）

如果这［存在一些心灵不能判定的数论问题］是真的，那么这意味着人类理性毫无道理可言，因为它出了它不能回答的问题，而又断然声称只有理性才能回答它们。这样一来，人类理性非但极不完美，而且在种意义上甚至是不一致的，与下面的事实构成尖锐的矛盾：那些得到了系统而完全的发展的数学分支（比如，一次与二次丢番图方程理论—后者有两个未知量）显示出惊人程度的优美与完满。在这些领域里，通过全然出人意料的规律与过程（如二次互反律、欧几里德算法、连分数等等），我们获得了解决所有相关问题的手段，不仅如此，这些手段还以最优美和纯粹可行的方式解决问题（例如，由简单的表达式产生所有的解）。这些事实似乎核证了可以称之为“理性乐观主义”的观点。

［因此，心灵胜过所有的机器。］

类似地，推广的哥德尔第二不完全性定理，如定理11，也可以为哥德尔“心灵胜过所有的机器”的反机械主义主张提供支持，其论证与之类似4与之不同的是：递归可枚举理论因其公理集是递归的，可以毫无问题地形式化为公理系统，从而等价于一台足够强的定理证明机器；但非递归可枚举理论因其公理集是非递归可枚举的，无法形式化为公理系统，但因其是可定义的，足够强的定理证明机器至少可以“用算术语言谈论”它。：如果心灵可以形式化为一台足够强的、可以谈论非递归可枚理论的机器，那么根据推广的哥德尔第二不完全性定理就会产生一个新的算术语句，如Σn-可靠性，该机器无法证明它从而也就“不知道”它是真的，但心灵知道它是真的；于是，或者心灵胜过所有的机器，或者存在一些心灵不能判定的算术语句；再根据理性乐观主义，可以排除“存在一些心灵不能判定的算术语句”，因此心灵胜过所有的机器。

6.3 对数学家地位的辩护

同样借助于哥德尔第二不完全性定理3，Penrose 先后在[17，18]中提出、论证并完善了对“数学洞察力（insight）不能被计算地（algorithmically）模仿”的反机械主义主张。他将数学洞察力定义为数学家生成数学命题和证明以及能够理解彼此证明的方法。其具体论证如下5为增强可读性，该论证以及下文两个子论证的具体表述略有删改。：

(1) 假如存在某个公理系统S 可以抓住数学洞察力所必需的思想。

(2) 那么，根据哥德尔第二不完全性定理，S 不能证明S 是一致的。

(3)［富有数学洞察力的］我们知道S 是一致的。

(4) 由于S 可以抓住我们的思想［数学洞察力所必需的思想］，所以S 可以证明S 是一致的。

(5) 矛盾！因此，不存在如此的公理系统。

如果(3)是可信的，那么上述论证将是非常可靠的。于是Penrose 分两种情形论证了(3)：(a)我们知道S 抓住了我们的思想；(b)我们不知道S 抓住了我们的思想。关于第一种情形，其论证比较简单：

(3a.1) 我们知道我们的思想是一致的。

(3a.2) 因此，如果我们知道S 抓住了我们的思想，那么我们便知道S 是一致的。

关于第二种情形，Penrose 在一定程度上求助了人类理性思维的可靠性：

(3b.1) 根据定义，S 由公理集和推理规则集组成。

(3b.2) 每个公理的有效性都可以被我们查证。

(3b.3) 并且，每个推理规则的有效性也可以被我们查证，不然人类的推理将会建立在无把握的推理规则之上，而这是难以置信的。

(3b.4) 由于我们知道每个公理和推理规则都是有效的，所以我们知道S 是一致的。

可以看到在这两种情形的论证中，Penrose 的部分想法与哥德尔的理性乐观主义有异曲同工之妙。

从Penrose 的“数学洞察力不能被计算地模仿”的反机械主义主张，我们可以更进一步：富有数学洞察力的数学家不可能被计算机所取代，因此数学家之所以为数学家的主体地位就难为计算机所撼动。这一整个论证过程是以哥德尔第二不完全性定理为基础的，将其中的“公理系统S”替换为“一台足够强的定理证明机器”可以得到一个本质相同的论证，而这个替换后的论证可以如上小节内容一样略经修改得到一个以推广的哥德尔第二不完全性定理为基础的新论证，从而为数学家的地位提供类似的辩护。

7 问 题

本文将哥德尔不完全性定理进行了充分的推广，并基于这些推广的哥德尔不完全性定理重新审视了哥德尔不完全性定理产生的哲学影响。与此同时，有两个尚未解决但比较重要的问题需要指出以待进一步研究。第一个问题与推广的哥德尔第二不完全性定理有关。推广的哥德尔第一不完全性定理既有与Γ-可靠性相关的，也有与n-一致性相关的。而所证推广的哥德尔第二不完全性定理却全是与Γ-可靠性相关的，那么是否也有与n-一致性相关的推广的哥德尔第二不完全性定理？

问题1.设T是包含PA 的、Σm+1-可定义的（Πm-可定义的）的理论。如果T是n-一致的，那么Con(T)是否成立？如果成立，那么m，n差值又可以是多少？

第二个问题与可证自身一致性理论需要满足的条件有关。第5 节定义的T 和S都是可证自身一致性的特殊理论，于是不禁要问：

问题2.如果一个理论可证自身一致性，那么对其需要满足的充分条件有没有一个更一般的刻划？