基于蒙特卡罗模拟的PPP项目投资风险分析

摘要：当前，PPP模式在国内进行得如火如荼，各路资本纷纷摩拳擦掌。对于社会资本参与者而言，需要对投资项目进行诸多评价，尤其是针对收益与风险的财务评价。传统的投资项目评价模型已发展得非常成熟，有着整套的思路和方法，但对于PPP项目，进行经济效益分析通常仅从预测来的固定数据着手，鲜有考虑项目面临的各种风险及存在的众多不确定性。本文旨在通过对拟投资项目进行蒙特卡罗模拟分析，综合考虑各方面因素，给PPP投资项目提供一个进行财务评价的新思路。

关键词：PPP项目;投资风险;蒙特卡罗模擬

PPP模式最早起源于欧洲，由政府授权私人资本参与投资建设并运营公共基础设施，以缓解政府资金吃紧时投资基础设施建设的压力。最近几年，地方政府债务压力剧增，迫使传统的工程承包施工模式向投资拉动转型，再加上财政部的极力推行，更使得这种投资模式在公共基础设施方面的参与度越来越高。基础设施领域的投融资模式从地方政府融资平台主导，逐步向平台融资为主、PPP模式为辅的局面转变，有些地方甚至出现两种融资模式并行的情况。然而，PPP项目整个生命周期存续时间长，项目参与者多，组织结构复杂，面临的不确定性因素很多，尤其是在项目建成投产后的运营阶段，投资者最为关注的莫过于评价和监控项目收益是否已达到预期。

一、风险分析的必要性

在项目实践中，国内众多对PPP项目进行投资评价的案例多侧重于确定某个价格水平，而现实是，外部环境如政府履约能力下降、材料价格上涨、技术更新、政策变化、产品标准升级等因素的变化，使得一个简单的道路施工项目都无法按照招标价格完全锁定，更遑论长达20—30年经营期的PPP项目了。如果投资者在进行投资效益分析时，仅按照某些给定的数据资料进行财务分析和测算，必然与实际存在较大出入，因此，投资前分析拟投资项目的风险和不确定性是非常重要且有必要的。

二、分析方法的选择

当下，国内对传统投资项目进行财务评价多参考建设部和发改委发布的《建设项目经济评价方法与参数》（2006第三版），而PPP作为一种新的投融资模式，尚未形成自有的一套评价体系。在《PPP项目财务评价实战指南》中，蒲明书等学者以传统常规投资项目分析评价方法为基础，初步构建了PPP项目财务评价模型，即根据市场调查与预测得来的数据，在不同层面（项目全投资、项目自有资金、投资各方现金）编制能够满足不同分析目的的财务报表，在此基础上对项目作出评价，来满足投资各方不同的决策需求。财务分析的基础是对财务报表进行分析，而评价投资项目的可行性更是依赖于根据项目各期资金流入流出情况编制的预测现金流量表。该书参照方法与参数给出了三个评价PPP项目的指标，包括动态投资回收期、净现值及内部收益率。

然而，在方法与参数一书中并未补充具体的风险分析及有关的指标评价，《PPP项目财务评价实战指南》虽然略有提及，但也并未给出具体的处理过程。参阅相关文献了解到分析项目风险的方法有两种基本途径：一是比较传统的方法，即对相应评价指标做适当修正;二是采用技术分析的方法，如敏感性分析法和概率树法，但是这两种方法的缺点显而易见，它们仅能围绕单个因素的变动进行分析或只能模拟有限场景，不能对所有可能发生的情况进行测算，并且在复杂的环境条件下，目标值同时受诸多因素的影响，单一因素分析也不能反映具体实际。蒙特卡罗模拟可以同时对多个变量进行成千上万次模拟，这就相当于整个测算过程中该项目实施了成千上万次，而输入的影响目标值的变量如投资总额、折现率、年均现金净流量则是随机的，每模拟一次都会给出一个目标值，在此基础上计算目标值的概率分布图，同时可以根据计算出来的项目标准差及变异系数确定目标值偏离预期的程度，由此评价目标项目的风险高低。经过考量分析，对PPP投资项目进行财务评价选择蒙特卡罗模拟方法是合适的。

三、蒙特卡罗模拟分析方法的具体实施

对投资项目进行蒙特卡罗模拟分析：第一，确定目标变量，笔者在此选取的是前述三个评价指标中的净现值指标;第二，确定影响目标变量的各项经济因素，并分析各因素的参数特征;第三，确定目标值与各变量之间的影响关系，建立评价指标计算模型;第四，模拟运算，并得出合适数量的样本值;第五，对样本值进行统计分析，并对模拟结果进行解释。

以某河道治理PPP项目为例，蒙特卡罗模拟的分析步骤如下：①根据历史资料分析相关数据信息，评估相关参数特征，确定概率分布，如项目初始投资额符合正态分布，年均净现金流符合三角分布，利率（折现率）符合均匀分布，由此产生各参数每次模拟时的随机数;②建立财务风险评价模型;③进行模拟运算，通过查阅相关文献，结合项目实际情况，模拟5 000次得到的样本值足以对项目风险进行客观分析与评价;④对5 000次模拟得到的样本值进行统计分析，求出项目净现值指标的概率分布;⑤分析评价目标项目风险水平和预期盈利能力。

四、案例分析

（一）案例资料

某投资项目为城市河道治理工程，不具备独立的商业经营条件，采用政府购买服务模式以保证SPV公司合理利润。项目选择“股权合作+BOT”的PPP模式，合作期限20年（其中建设期2年，经营期18年），政府在合作期10年内完成社会资本股权回购。20年合作期满由SPV公司将全部资产无偿移交政府指定机构。

1.项目总投资估算约45 413万元（实际操作中以审计局审计决算值作为政府财政支付的最终依据），其中建设投资43 650万元，建设期融资费用约1 763万元。银行融资费率用按现行五年期以上银行贷款基准利率即4.9%（随利率变化而同步调整）。

2.根据政府资金支付的不同用途，政府财政支出按股权回购费用、SPV融资还本付息费以及运营缺口补助费等三部分进行测算。

第一，股权回购费用。按照政府在合作期10年内完成社会资本股权回购（回购方式和比例暂按合作期第6年至第10年等比例回购），资本金内部收益率执行5年期以上银行贷款基准利率，从而测算社会资本股权回购支付资金。经计算股权合作期10年内政府支付股权回购费用约12 370万元。

第二，SPV融资还本付息费。贷款期限20年（含建设期2年），贷款偿还按照等额还本、利息照付方式，按照5年期以上银行贷款基准利率4.9%（随利率变化而同步调整）测算，20年合作期内政府支付SPV融资还本付息费总额约52 352万元。

第三，运营缺口补助费。不考虑折旧摊销，按照4.9%年静态利润率（执行5年期以上银行贷款基准利率），以运营成本为基数核算合理利润，并考虑扣除税金及附加后，计算运营缺口补助（即运营财政补贴，列入年度财政预算），经核算20年合作期内政府支付运营缺口补助约936万元。

综上，20年合作期內政府财政支出总额约65 658万元（折现值约41 494万元），包括股权回购费用约12 370万元，SPV融资还本付息费约52 352万元，运营缺口补助费约936万元。

（二）风险因素识别

社会资本方根据政府方提出的合作条件，结合所掌握的相关基础资料，需要作出是否参与该项目的投资决策。决策中最大的不确定性因素与项目投资总额、资本成本、及年均净现金流量有关，而后者与运营成本有关。说明如下：

由于政府支付的股权回购金额、融资还本付息费及运营缺口补助金额是固定的，这些作为项目全投资的现金流入不存在政府违约风险以外的、由于不确定性导致流入减少的风险，因此，在进行蒙特卡罗模拟分析时可以不予考虑;在现金流出方面，投资额看似固定，但实际操作中以审计局审计决算值作为政府财政支付的最终依据，而根据经验数据，由于对项目所处环境了解不足、材料人工费用等成本上涨、施工技术要求提高等因素，导致最终决算金额与前期合同金额存在较大出入的情况非常普遍;另外，本案例投资施工方案中测算每年的运营成本除试运营期外基本稳定在某一固定值，而事实是，在较长的一段时期，运营成本可能与物价指数相挂钩呈逐年上涨趋势或围绕某一固定值上下波动，受这些不确定性因素影响，项目净现金流出可能会波动上涨而不会是固定在某一特定值上。此外，银行利率在漫长的经营期内受国家财政政策调整的影响，也不可能被完全锁定。这些不确定性因素都会影响到项目现金净流量，进而影响到社会资本方投资该项目的效率与效果。

（三）风险因素的概率分布假定

为作出投资决策，社会资本方需进行项目全投资现金流分析，计算项目全投资的财务净现值。为反映不确定性因素对项目投资效益的影响，进行蒙特卡罗模拟分析。在蒙特卡罗模拟分析中，将项目总投资、项目折现率与年均净现金流量均取为输入变量，项目全投资净现值取为目标变量，通过蒙特卡罗模拟得到项目全投资净现值的若干样本值，进而计算其统计特征量。

在蒙特卡罗模拟中，假定项目总投资符合期望值为45 413，标准差为1 500的正态分布;折现率选用融资成本4.9%，随银行利率调整上下浮动，根据利率调整数据资料分析，假定符合3.9%—5.9%的均匀分布;年均净现金流量根据实施方案测算，假定符合最大值为5 929万元，最小值2 070万元，最可能值为3 135的三角分布（三角分布各值由项目施工方案给出的各特定值测算得出）。

（四）选定实现相关参数变量的函数

由于上述参数分别符合正态分布、均匀分布与三角分布，故在EXCEL表格中可以直接采用NORM.INV、RAND（）函数来产生随机数。在EXCEL中实现三角分布需要固定前一次所取的随机数以避免数据由于表单操作而发生变化。相关参数的表现形式如下：

1.项目初始投资：C0=NORM.INV（RAND（），45413，1500）

2.折现率：

3.年均净现金流量：C1=2070+（5929-2070）×IF（RAND（）<

4.项目净现值NPV：NPV（rate， value 1，value2，……）

（五）模拟运算过程

笔者利用EXCEL进行了模拟运算，涉及的项目初始投资、项目折现率以及年均净现金流量等数据均由计算机系统随机产生，每次运算均产生相应的净现值。对5 000个随机得来的净现值进行统计分析，以找寻其统计特征及规律;将净现值下限设定为0，并对其进行降序排列，计算出净现值大于0的累计概率;同时，利用EXCEL中的AVERAGE函数及STDEV函数分别求出该组数据的均值及标准差，利用MAX（）及MIN（）函数求出5 000次模拟净现值的极大值及极小值。

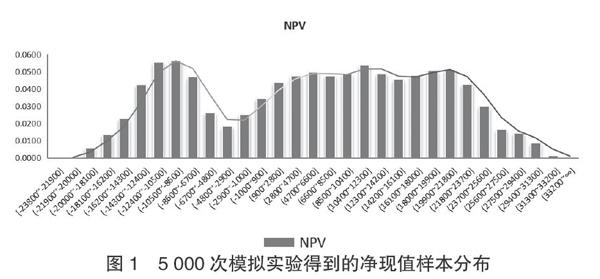
利用该组数据绘制直方图，就得到了被研究的该PPP投资项目的净现值样本分布图（如图1）。

本文利用用蒙特卡罗模拟法在计算机模拟5 000次，得到拟投资项目净现值NPV如下的统计特征：最大值为31 717.13万元，最小值为-23 243.56万元，平均值为4 066.16万元，标准差为12 783.71万元，净现值出现在0—31 717.13的概率为62.82%，净现值出现负数的概率为37.18%。同时，各数据偏离期望值的离散程度很高，该投资项目虽然可行但存在较大风险。

五、结语

本文利用EXCEL软件提供的函数功能，实现了蒙特卡罗模拟实验，通过案例给出了基于蒙特卡罗模拟的PPP项目投资风险分析的具体处理过程，并对项目作出评价。然而，本文在处理过程中仍有不足之处，在进行年净现金流测算时，为了简化过程，假定各年净现金流量满足符合某一数据特征的三角分布，而在该案例中，由于5—10年的股权回购，因而在这一阶段净现金流与其他各年存在较大差异，但本文中给予了模糊处理。

参考文献：

[1]蒲明书，等.PPP项目财务评价实战指南[M].北京：中信出版社，2016.

[2]国家发展改革委建设部.建设项目经济评价方法与参数（第三版）[M].北京：中国计划出版社，2006.

[3]向寿生，尚宇梅.Excel在投资项目概率分析中的应用[J].商业研究，2008（7）.

[4]梁磊.用EXCEL实现风险决策的蒙特卡罗模拟分析[J].科学技术与工程，2008（20）.

[5]谢岚.管理会计中EXCEL的高级应用：长期投资决策的蒙特卡罗模拟模型的设计与应用[J].财会信息化，2014（10）.

[6]连春茗，孟昭亮.PPP项目财务评价指标含义及其适用性的比较研究[J].中国工程咨询，2017（6）.

作者简介：渠文灵（1987—），女，山东郓城县人，会计师，硕士，主要从事财务工作研究。